Al igual que el pastel, puedes tener 2 trozos pequeños o un trozo el doble de grande y es la misma cantidad. De ahí que muchas fracciones sean equivalentes, como 2/5 y 4/10.


Cualquier número puede escribirse como una fracción
Escribe cualquier número entero mayor que 1 para convertirlo en una fracción ya que el número total de partes de cualquier entero indiviso es uno.
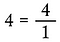
Multiplicar fracciones en línea recta
Multiplicar fracciones es fácil, sólo hay que multiplicar en línea recta.
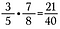
Nota: Los números mixtos deben convertirse primero en fracciones impropias, sigue leyendo para saber más sobre esto.
Multiplicar por cualquier forma de uno en cualquier momento
El número 1 se llama identidad multiplicativa porque podemos multiplicarlo por cualquier número y el número sigue siendo el mismo. Esto es importante para las fracciones porque a menudo necesitamos alterar la apariencia de una fracción sin cambiar realmente su valor.
Por ejemplo, puedo cambiar 1/3 en la fracción equivalente 3/9 multiplicando por 3/3.
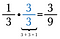
Sumar y restar partes de igual tamaño
Al sumar y restar fracciones los denominadores deben ser iguales. Esto tiene sentido. Si queremos combinar o restar partes debemos hablar de partes del mismo tamaño, de lo contrario se volvería confuso.
¿Entonces qué haces si tus fracciones no tienen los mismos tamaños?
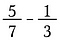
Multiplica por una forma de uno para cambiar los denominadores a un tamaño común. Esencialmente, estamos dividiendo las fracciones en trozos más pequeños hasta que tengan el mismo tamaño. Esto se llama encontrar un denominador común.
En realidad, cualquier denominador común servirá, pero la gente prefiere encontrar el más pequeño. En este caso, el número más pequeño en el que entran el 7 y el 3 sin que queden restos es el 21. Así que multiplica la primera fracción por 3/3 y la segunda por 7/7.
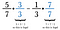
Si no se te ocurre el mínimo común denominador, siempre puedes multiplicar cada fracción por la denominación opuesta. A veces, como en este caso, ese resulta ser el mínimo común denominador. Si no lo es, simplemente reduce tu respuesta al final.
Una vez que los denominadores coinciden, resta los numeradores para obtener 8/21.
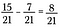
Esto funciona como cabría esperar. Pictóricamente, empieza con 15 piezas de 21 en total.

Quita el colorante de 7 de los 15 bloques azules.

Lo que deja 8/21 como se esperaba.
Cambia primero los números mixtos
Un número mixto es la combinación de un número entero y una fracción.
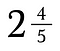
Los números mixtos no juegan bien con otras fracciones. Es una buena idea convertirlos en fracciones impropias primero.
Nota: Una fracción impropia es una fracción cuyo numerador es mayor que su denominador por lo tanto tiene un valor mayor que uno.
Convertir un número mixto es realmente una adición
Para convertir 2 y 4/5 en una fracción impropia suma 2 + 4/5.
Paso 1: Comienza reescribiendo 2 como 2/1.
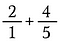
Paso 2: Multiplicar 2/1 por 5/5 para hacer una fracción equivalente de 10/5 que tenga el denominador común deseado de 5.
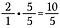
Paso 3: Sumar 10/5 + 4/5.
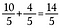
Nuestro resultado es la fracción impropia equivalente 14/5.
Para volver a convertir a un número mixto realiza la división. Por ejemplo, 5 entra en 14 dos veces (ya que 5 x 2 = 10) y quedan 4 trozos.
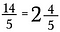
Comparar fracciones usando el producto cruzado
Supongamos que queremos determinar cuál es mayor: 5/12 o 6/13.
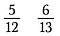
Primer paso: Multiplica una diagonal y escribe el producto sobre el numerador.
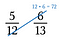
Paso dos: Multiplica la otra diagonal y escribe su producto sobre su numerador.
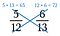
Paso tres: Compara los productos. El lado con el producto mayor es la fracción mayor. Así que en este caso, 5/12 es menor que 6/13.
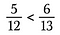
También podemos determinar si las fracciones son iguales utilizando productos cruzados.
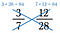
El producto cruzado de 3/7 y 12/28 son ambos 84, por lo tanto 3/7 = 12/28.
Cancela cualquier cosa que divida a uno
Lo mejor de las fracciones es que puedes encontrar muchas oportunidades para cancelarlas. Lo que las hace rápidas y fáciles de manejar.
Supongamos que tengo la fracción 8/10. Tanto 8 como 10 pueden reescribirse con 2 como factor.
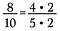
Como 2/2 = 1, puedo cancelar los 2 dejando 4/5 como fracción reducida.
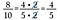
Utiliza esta estrategia para facilitar también la multiplicación de fracciones.
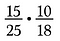
Comienza reescribiendo cada uno de los números en factores.
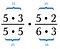
Cancela cualquier pareja de números que se divida por 1. Por ejemplo, 5/5 = 1.
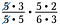
Tengo otro par de 5 y un par de 3 que también se dividen por 1.
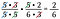
¡Ups! Podría haber reescrito 6 como 2 x 3 y haber anulado un par de 2’s. No pasa nada si se te escapa un factor, sigue hasta que los consigas todos.
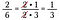
Si hubiera multiplicado 15/25 por 10/18 directamente hubiera sido mucha aritmética, al usar la cancelación reduzco previamente las fracciones y hago más sencilla la multiplicación.
Utilizar la multiplicación para dividir fracciones
El concepto de dividir fracciones es fácil con ejemplos sencillos como:

Hay dos mitades en un entero, por tanto hay 10 mitades en 5 enteros.
Pero el concepto se complica con fracciones más complicadas.
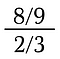
Para resolver este problema utilizaremos dos hechos:
- Podemos multiplicar por cualquier forma de uno (i.e cualquier cosa por encima de sí mismo)
- Al multiplicar por el recíproco de 3/2, que es 2/3, se obtiene 1 mediante la cancelación
Paso uno: Comienza multiplicando por el recíproco sobre sí mismo.
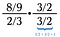
Ahora tenemos dos problemas más pequeños que resolver (azul y verde).
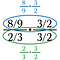
Paso dos: Anule todo lo que divida a 1 en la fracción inferior (verde). Esto debería dar siempre como resultado 1.

Ahora nos queda el problema superior por resolver.
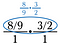
Paso tres: Utiliza la cancelación para reducir previamente la fracción. Después de hacer estas reducciones, multiplica a través para obtener 4/3.

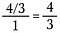
Ahorro
Esta es la mecánica de mano larga de «voltear y multiplicar.»
Podemos omitir la multiplicación por el recíproco en el fondo ya que siempre se cancela a 1. Por lo tanto todo lo que hay que hacer es multiplicar el numerador por el recíproco del denominador.

Bonus: Teoría, por si te interesa…
¡Gran pregunta! Para generalizar, haz dos fracciones utilizando las letras a, b, c y d para representar cuatro números diferentes.
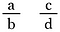
Multiplica ambas fracciones por b-d (esto nos permitirá anular los denominadores).
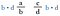
Ahora cancela las b de la izquierda y las d de la derecha ya que se dividen a 1. Ya no tenemos fracciones, sólo los productos d-a y c-b.
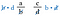
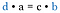
Vuelve a mirar las fracciones originales. Son los mismos productos que si hubiéramos multiplicado las diagonales. Por tanto, el atajo es comparar el producto cruzado.
❤ ESTÁ CONECTADO ❤
¡Mantente al día de todo lo que hace Math Hacks!