Recientemente, un compañero me hizo algunas preguntas como «¿por qué tenemos tantas funciones de activación?», «¿por qué es que una funciona mejor que la otra?», «¿cómo sabemos cuál usar?», «¿es matemática dura?» y así sucesivamente. Así que pensé, ¿por qué no escribir un artículo sobre él para aquellos que están familiarizados con la red neuronal sólo en un nivel básico y es, por tanto, preguntando acerca de las funciones de activación y su «por qué-cómo-matemáticas!».
NOTA: Este artículo asume que usted tiene un conocimiento básico de una «neurona» artificial. Recomendaría leer los fundamentos de las redes neuronales antes de leer este artículo para una mejor comprensión.
Funciones de activación
¿Entonces qué hace una neurona artificial? Sencillamente, calcula una «suma ponderada» de su entrada, añade un sesgo y luego decide si debe «dispararse» o no ( sí, claro, esto lo hace una función de activación, pero sigamos la corriente por un momento).
Así que considera una neurona.
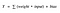
Ahora, el valor de Y puede ser cualquier cosa desde -inf hasta +inf. La neurona realmente no conoce los límites del valor. Entonces, ¿cómo decidimos si la neurona debe disparar o no ( por qué este patrón de disparo? Porque lo aprendimos de la biología que es la forma en que el cerebro funciona y el cerebro es un testimonio de trabajo de un sistema impresionante e inteligente ).
Decidimos añadir «funciones de activación» para este propósito. Para comprobar el valor Y producido por una neurona y decidir si las conexiones externas deben considerar esta neurona como «disparada» o no. O mejor digamos – «activada» o no.
Función de paso
Lo primero que se nos ocurre es ¿qué tal una función de activación basada en el umbral? Si el valor de Y está por encima de un determinado valor, declararlo activado. Si es menor que el umbral, entonces di que no lo está. Hmm genial. Esto podría funcionar!
Función de activación A = «activado» si Y > umbral sino no
Alternativamente, A = 1 si y umbral, 0 en caso contrario
Bueno, lo que acabamos de hacer es una «función escalonada», ver la siguiente figura.
Su salida es 1 («activado») cuando el valor > 0 (umbral) y emite un 0 («no activado») en caso contrario.
Genial. Así que esto hace una función de activación para una neurona. No hay confusiones. Sin embargo, hay ciertos inconvenientes con esto. Para entenderlo mejor, piensa en lo siguiente.
Supón que estás creando un clasificador binario. Algo que debe decir un «sí» o un «no» ( activar o no activar ). ¡Una función Step podría hacer eso por ti! Eso es exactamente lo que hace, decir un 1 o un 0. Ahora, piense en el caso de uso en el que usted querría que múltiples neuronas de este tipo se conectaran para traer más clases. Clase1, clase2, clase3, etc. ¿Qué ocurrirá si se «activa» más de una neurona? Todas las neuronas emitirán un 1 (de la función de paso). ¿Ahora qué decidirías? ¿De qué clase se trata? Hmm difícil, complicado.
Querrías que la red activara sólo 1 neurona y las demás fueran 0 ( sólo así podrías decir que clasificó correctamente/identificó la clase ). Ah! Esto es más difícil de entrenar y converger de esta manera. Hubiera sido mejor que la activación no fuera binaria y que dijera «50% activado» o «20% activado» y así sucesivamente. ¡Y entonces si se activa más de 1 neurona, se podría encontrar qué neurona tiene la «mayor activación» y así sucesivamente ( mejor que max, un softmax, pero dejémoslo por ahora).
En este caso también, si más de 1 neurona dice «100% activado», el problema sigue persistiendo.Lo sé! Pero … ya que hay valores intermedios de activación para la salida, el aprendizaje puede ser más suave y más fácil ( menos wiggly ) y las posibilidades de más de 1 neurona de ser 100% activado es menor en comparación con la función de paso mientras que la formación ( también dependiendo de lo que usted está entrenando y los datos ).
Ok, así que queremos algo para darnos intermedio ( analógico ) valores de activación en lugar de decir «activado» o no ( binario ).
Lo primero que nos viene a la cabeza sería la función lineal.
Función lineal
A = cx
Una función rectilínea donde la activación es proporcional a la entrada ( que es la suma ponderada desde la neurona ).
De esta forma, da un rango de activaciones, por lo que no es una activación binaria. Definitivamente podemos conectar algunas neuronas juntas y si más de 1 se dispara, podríamos tomar el máximo ( o softmax) y decidir en base a eso. Así que eso también está bien. Entonces, ¿cuál es el problema con esto?
Si estás familiarizado con el descenso de gradiente para el entrenamiento, te darás cuenta de que para esta función, la derivada es una constante.
A = cx, la derivada con respecto a x es c. Eso significa, que el gradiente no tiene ninguna relación con X. Es un gradiente constante y el descenso va a ser en gradiente constante. Si hay un error en la predicción, los cambios realizados por la retropropagación son constantes y no dependen del cambio en la entrada delta(x) !!!
¡Esto no es tan bueno! ( no siempre, pero tenedme en cuenta ). También hay otro problema. Piensa en capas conectadas. Cada capa es activada por una función lineal. Esa activación a su vez pasa al siguiente nivel como entrada y la segunda capa calcula la suma ponderada sobre esa entrada y ésta a su vez, se dispara en base a otra función de activación lineal.
¡No importa cuántas capas tengamos, si todas son de naturaleza lineal, la función de activación final de la última capa no es más que una función lineal de la entrada de la primera capa! Párate un poco y piénsalo.
Eso significa que estas dos capas ( o N capas ) pueden ser sustituidas por una sola capa. ¡Ah! Acabamos de perder la capacidad de apilar capas de esta manera. No importa cómo apilemos, toda la red sigue siendo equivalente a una sola capa con activación lineal ( una combinación de funciones lineales de forma lineal sigue siendo otra función lineal ).
Sigamos adelante, ¿quieres?
Función Sigmoide
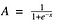
Bueno, esto parece suave y «como una función escalonada». ¿Cuáles son los beneficios de esto? Piénsalo por un momento. Lo primero es que es de naturaleza no lineal. Las combinaciones de esta función también son no lineales. Genial. Ahora podemos apilar capas. ¿Y las activaciones no binarias? Sí, ¡eso también!. Dará una activación analógica a diferencia de la función escalonada. Tiene un gradiente suave también.
Y si te das cuenta, entre los valores de X -2 a 2, los valores de Y son muy empinados. Lo que significa, que cualquier pequeño cambio en los valores de X en esa región hará que los valores de Y cambien significativamente. Ah, eso significa que esta función tiene una tendencia a llevar los valores de Y a cualquier extremo de la curva.
¿Parece que es bueno para un clasificador teniendo en cuenta su propiedad? Sí, lo es. Tiende a llevar las activaciones a ambos lados de la curva ( por encima de x = 2 y por debajo de x = -2 por ejemplo). Haciendo claras distinciones en la predicción.
Otra ventaja de esta función de activación es que, a diferencia de la función lineal, la salida de la función de activación siempre va a estar en el rango (0,1) en comparación con (-inf, inf) de la función lineal. Así que tenemos nuestras activaciones limitadas en un rango. Bien, no va a explotar las activaciones entonces.
Esto es genial. Las funciones sigmoides son una de las funciones de activación más utilizadas hoy en día. Entonces, ¿cuáles son los problemas con esto?
Si te das cuenta, hacia cualquier extremo de la función sigmoide, los valores de Y tienden a responder muy poco a los cambios en X. ¿Qué significa eso? El gradiente en esa región va a ser pequeño. Esto da lugar a un problema de «gradientes de fuga». Hmm. Entonces, ¿qué sucede cuando las activaciones llegan cerca de la parte «casi horizontal» de la curva en ambos lados?
El gradiente es pequeño o se ha desvanecido (no puede hacer un cambio significativo debido al valor extremadamente pequeño). La red se niega a seguir aprendiendo o es drásticamente lenta ( dependiendo del caso de uso y hasta que el gradiente/computación es golpeado por los límites del valor de punto flotante ). Hay maneras de trabajar alrededor de este problema y sigmoide sigue siendo muy popular en los problemas de clasificación.
Función Tanh
Otra función de activación que se utiliza es la función tanh.
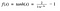
Hm. Esto se parece mucho a la sigmoidea. De hecho, ¡es una función sigmoidea escalada!

Ok, ahora esto tiene características similares a la sigmoidea que discutimos anteriormente. Es de naturaleza no lineal, ¡tan grande que podemos apilar capas! Está limitado al rango (-1, 1), por lo que no hay que preocuparse de que las activaciones exploten. Un punto a mencionar es que el gradiente es más fuerte para tanh que para sigmoide (las derivadas son más pronunciadas). Decidir entre el sigmoide o el tanh dependerá de su requisito de la fuerza del gradiente. Al igual que sigmoide, tanh también tiene el problema de gradiente de fuga.
Tanh es también una función de activación muy popular y ampliamente utilizada.
ReLu
Más tarde, viene la función ReLu,
A(x) = max(0,x)
La función ReLu es como se muestra arriba. Da una salida x si x es positivo y 0 en caso contrario.
A primera vista esto parecería tener los mismos problemas de la función lineal, ya que es lineal en el eje positivo. En primer lugar, ReLu es de naturaleza no lineal. ¡Y las combinaciones de ReLu también son no lineales! ( de hecho es un buen aproximador. Cualquier función puede ser aproximada con combinaciones de ReLu). Genial, esto significa que podemos apilar capas. Sin embargo, no está limitado. El rango de ReLu es [0, inf). Esto significa que puede volar la activación.
Otro punto que me gustaría discutir aquí es la escasez de la activación. Imagina una gran red neuronal con muchas neuronas. El uso de una sigmoide o tanh hará que casi todas las neuronas se disparen de forma analógica ( ¿recuerdas? ). Eso significa que casi todas las activaciones serán procesadas para describir la salida de la red. En otras palabras, la activación es densa. Esto es costoso. Idealmente querríamos que unas pocas neuronas de la red no se activaran y así hacer que las activaciones sean dispersas y eficientes.
ReLu nos da este beneficio. Imaginemos una red con pesos inicializados aleatoriamente ( o normalizados ) y que casi el 50% de la red arroja una activación 0 debido a la característica de ReLu ( salida 0 para valores negativos de x ). Esto significa que un menor número de neuronas están disparando ( activación dispersa ) y la red es más ligera. Woah, ¡qué bien! ¡ReLu parece ser impresionante! Si lo es, pero nada es impecable.. Ni siquiera ReLu.
Debido a la línea horizontal en ReLu ( para X negativo ), el gradiente puede ir hacia 0. Para las activaciones en esa región de ReLu, el gradiente será 0 debido a que los pesos no se ajustarán durante el descenso. Es decir, las neuronas que entren en ese estado dejarán de responder a las variaciones de error/entrada (simplemente porque el gradiente es 0, nada cambia). Esto se llama el problema de ReLu moribundo. Este problema puede hacer que varias neuronas simplemente mueran y no respondan haciendo que una parte sustancial de la red sea pasiva. Hay variaciones en ReLu para mitigar este problema simplemente convirtiendo la línea horizontal en un componente no horizontal, por ejemplo y = 0.01x para x<0 hará que sea una línea ligeramente inclinada en lugar de una línea horizontal. Esto es ReLu con fugas. También hay otras variaciones. La idea principal es dejar que el gradiente no sea cero y se recupere durante el entrenamiento eventualmente.
ReLu es menos costoso computacionalmente que tanh y sigmoide porque implica operaciones matemáticas más simples. Ese es un buen punto a considerar cuando estamos diseñando redes neuronales profundas.
Ok, ¿ahora cuál usamos?
Ahora, qué funciones de activación usar. ¿Significa que sólo usamos ReLu para todo lo que hacemos? ¿O sigmoide o tanh? Bueno, sí y no. Cuando sabes que la función que estás tratando de aproximar tiene ciertas características, puedes elegir una función de activación que aproximará la función más rápidamente, lo que lleva a un proceso de entrenamiento más rápido. Por ejemplo, una sigmoidea funciona bien para un clasificador ( vea el gráfico de la sigmoidea, ¿no muestra las propiedades de un clasificador ideal? ) porque aproximar una función clasificadora como combinaciones de sigmoides es más fácil que quizás ReLu, por ejemplo. Lo que llevará a un proceso de entrenamiento y convergencia más rápido. También puede utilizar sus propias funciones personalizadas!. Si usted no sabe la naturaleza de la función que está tratando de aprender, entonces tal vez yo sugeriría empezar con ReLu, y luego trabajar hacia atrás. ReLu funciona la mayor parte del tiempo como un aproximador general!
En este artículo, traté de describir algunas funciones de activación utilizadas comúnmente. Hay otras funciones de activación también, pero la idea general sigue siendo la misma. La investigación de mejores funciones de activación está todavía en curso. Espero que hayas entendido la idea detrás de la función de activación, por qué se usan y cómo decidimos cuál usar.