Introducción
Esta página revisa la ecuación de continuidad, que refuerza la conservación de la masa en un análisis euleriano. Esto no es estrictamente una descripción del comportamiento de los materiales, pero la ecuación resultante se utiliza a menudo como una identidad para manipular algebraicamente los modelos constitutivos que describen el comportamiento de los materiales. Por tanto, merece la pena repasarla. También es fundamental para el análisis del flujo de fluidosporque los análisis clásicos de fluidos no pueden ser lagrangianos ya que las posiciones de todas las partículas del fluido en \(t = 0\) son desconocidas.
Conservación de la masa
La ecuación de continuidad refleja el hecho de que la masa se conserva en cualquier análisis de mecánica continua no nuclear. La ecuación se desarrolla sumando la velocidad a la que la masa entra y sale de un volumen de control, y estableciendo el flujo neto de entrada igual a la velocidad de cambio de la masa dentro de él. Esto se demuestra en la figura siguiente.
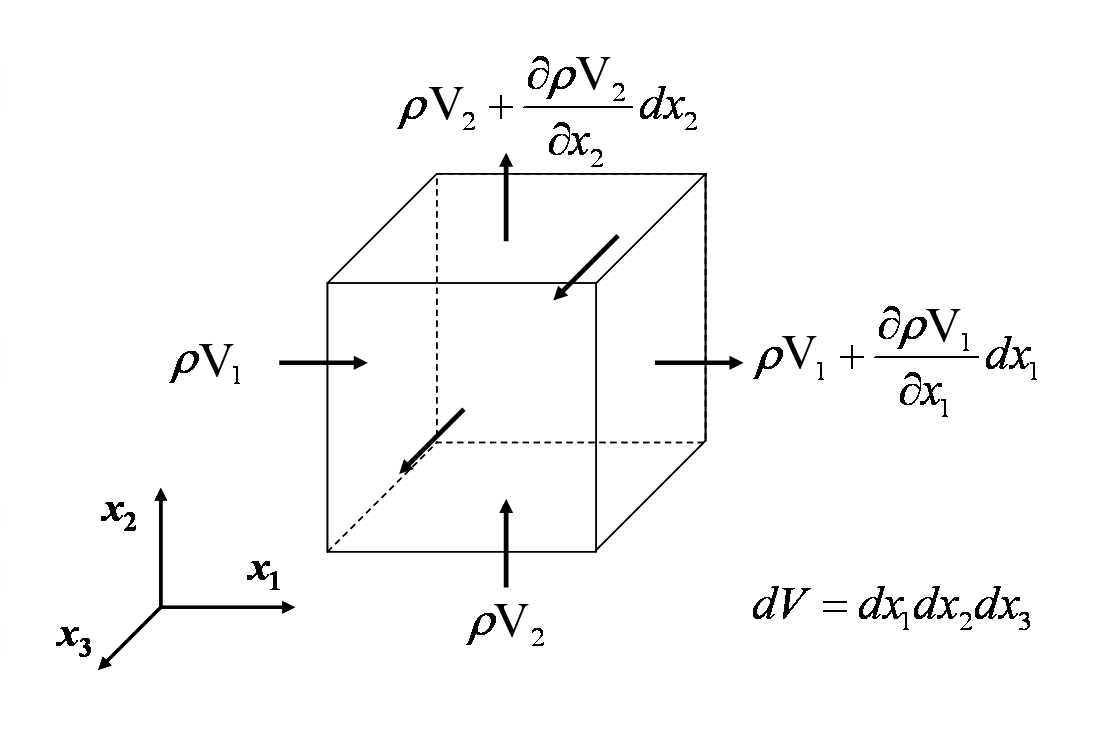
Calculando todos los caudales de masa que entran y salen del volumen de control diferencial, se obtiene
\
Cancelando los términos y dividiendo por \(dx_1 dx_2 dx_3\) da
\
y reordenando da
\
Esto se puede escribir de forma concisa como
\

Puntos importantes
Estas son las formas finales, completa y más general de la ecuación de continuidad que hace cumplir la conservación de la masa. Se aplica a todos los materiales, no sólo a los fluidos. Así que también se aplica a los sólidos. Obsérvese que es una única ecuación escalar y que es de naturaleza euleriana porque los términos del gradiente son \({parcialmente \ sobre \parcialmente x_i}), no \({parcialmente \ sobre \parcialmente X_i}).
Uno podría preguntarse si existe una contrapartida lagrangiana a la forma euleriana de esto. La hay. Se suele escribir como
\
Esto simplemente establece que el trozo diferencial de masa en el estado deformado\(\rho \, dV\) debe ser igual a su valor original\(\rho_o dV_o\) en el estado no deformado.
Hay varios casos especiales de la ecuación de continuidad.La primera ocurre cuando el flujo es de estado estacionario. En este caso, la derivada con respecto al tiempo es cero, quedando.
El segundo caso especial es el de la incompresibilidad, es decir \En este caso la derivada con respecto al tiempo es cero y \(\rho\) puede ser factorizado fuera de la ecuación dejando sólo
\
Este resultado es lo suficientemente simple que a menudo se expande.
\
Nótese que esto no es más que \text{tr}({\bf D}) = 0\) para el caso de materiales incompresibles.

Derivada de materiales
Lo siguiente es digno de mención porque permite separar la densidad y el vector velocidad. El primer paso es aplicar la regla del producto al término de divergencia en la ecuación de continuidad.
\NY luego notar que\N({parcial \rho \ sobre \parcial t} + {\bf v}\cdot \nabla \rho\) es sólo la derivada material de la densidad,\N({D \rho \ sobre D t}\).
Así que la ecuación de continuidad también puede escribirse como
\
Si el material es incompresible, entonces \(\rho\) no puede cambiar, así que( {D \rho \over D t} \) debe ser cero, dejando
\
Y luego dividir por \(\rho\) (ya que no es cero) para obtener
\

Ecuación de continuidad Ejemplo
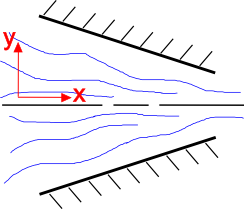
Es intuitivo que el flujo de fluido se acelera a medida que la sección transversal areadecreases, como se muestra a la derecha. La ecuación de continuidad lo explica. La ecuación de continuidad para esta situación es
Comienza observando la componente y del flujo, \(v_2\). La geometría de la tobera convergente obliga a la componente \2 a fluir hacia arriba cuando \2 es 0 y a fluir hacia abajo cuando \2 es 0. Por lo tanto, \ (v_2 \gt 0\) cuando \ (y \gt 0\) y \ (v_2 \lt 0\) cuando \ (y \gt 0\).
El efecto neto de esto es que \({parcial v_2 \ sobre \parcial x_2} \t 0\) en la boquilla convergente.
Pero la ecuación de continuidad dicta que la suma de las dos derivadas parciales debe ser igual a cero. Por lo tanto, si la segunda es menor que cero, entonces
\aquí significa que el flujo de fluido debe estar acelerando.