Las ecuaciones de Lotka-Volterra describen un modelo ecológico depredador-presa (o parásito-huésped) que supone que, para un conjunto de constantes positivas fijas 
(la tasa de crecimiento de las presas), 
(la tasa a la que los depredadores destruyen las presas), 
(la tasa de mortalidad de los depredadores), y 
(la tasa a la que los depredadores aumentan consumiendo presas), se dan las siguientes condiciones.
1. Una población de presas 
aumenta a una tasa 
(proporcional al número de presas) pero simultáneamente es destruida por los depredadores a una tasa 
(proporcional al producto del número de presas y depredadores).
2. Una población de depredadores 
disminuye a una tasa 
(proporcional al número de depredadores), pero aumenta a una tasa 
(de nuevo proporcional al producto del número de presas y depredadores).
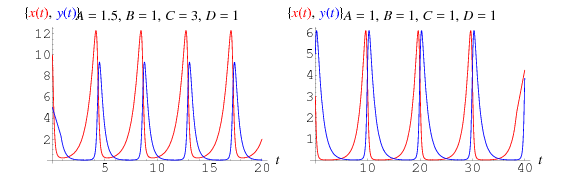
Esto da las ecuaciones diferenciales acopladas
 |
 |
 |
(1)
|
 |
 |
 |
(2)
|
cuyas soluciones se representan arriba, donde las presas se muestran en rojo, y los depredadores en azul. En este tipo de modelo, la curva de las presas siempre supera a la de los depredadores.
Los puntos críticos ocurren cuando 
, así que
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
El único punto estacionario se encuentra por tanto en 
.