Cuando los datos están listos para ser analizados, debe evaluarse a fondo, basándose en la inspección de los datos, si deben utilizarse métodos estadísticos para tratar los datos que faltan. Bell et al. se propusieron evaluar el alcance y el manejo de los datos faltantes en los ensayos clínicos aleatorios publicados entre julio y diciembre de 2013 en el BMJ, JAMA, Lancet y New England Journal of Medicine . El 95% de los 77 ensayos identificados informaron de algunos datos de resultados que faltaban. El método más utilizado para manejar los datos faltantes en el análisis primario fue el análisis de casos completos (45%), la imputación única (27%), los métodos basados en modelos (por ejemplo, modelos mixtos o ecuaciones de estimación generalizada) (19%) y la imputación múltiple (8%) .
El análisis de casos completos
El análisis de casos completos es un análisis estadístico basado en los participantes con un conjunto completo de datos de resultados. Los participantes con datos faltantes se excluyen del análisis. Como se describe en la introducción, si los datos que faltan son MCAR el análisis de casos completos tendrá una potencia estadística reducida debido al tamaño reducido de la muestra, pero los datos observados no estarán sesgados . Cuando los datos que faltan no son MCAR, la estimación del análisis de caso completo del efecto de la intervención podría estar basada, es decir, a menudo habrá un riesgo de sobreestimación del beneficio y subestimación del daño . Consulte la sección «¿Debe utilizarse la imputación múltiple para tratar los datos que faltan?» para obtener un análisis más detallado de la validez potencial si se aplica el análisis de caso completo.
Imputación simple
Cuando se utiliza la imputación simple, los valores que faltan se sustituyen por un valor definido por una determinada regla . Hay muchas formas de imputación simple, por ejemplo, la última observación trasladada (los valores perdidos de un participante se sustituyen por el último valor observado del participante), la peor observación trasladada (los valores perdidos de un participante se sustituyen por el peor valor observado del participante) y la imputación media simple . En la imputación de la media simple, los valores que faltan se sustituyen por la media de esa variable. El uso de la imputación simple suele dar lugar a una subestimación de la variabilidad porque cada valor no observado tiene el mismo peso en el análisis que los valores observados conocidos. La validez de la imputación única no depende de que los datos sean MCAR; la imputación única depende más bien de supuestos específicos de que los valores que faltan, por ejemplo, son idénticos al último valor observado . Estas suposiciones son a menudo poco realistas y la imputación única es, por lo tanto, un método potencialmente sesgado y debe utilizarse con gran precaución.
Imputación múltiple
Se ha demostrado que la imputación múltiple es un método general válido para tratar los datos que faltan en los ensayos clínicos aleatorios, y este método está disponible para la mayoría de los tipos de datos . En las siguientes secciones describiremos cuándo y cómo debe utilizarse la imputación múltiple.
¿Debe utilizarse la imputación múltiple para manejar los datos que faltan?
Razones por las que no debe utilizarse la imputación múltiple para manejar los datos que faltan
¿Es válido ignorar los datos que faltan?
El análisis de los datos observados (análisis de casos completos) ignorando los datos que faltan es una solución válida en tres circunstancias.
- a)
El análisis de casos completos puede utilizarse como análisis primario si las proporciones de datos perdidos están por debajo de aproximadamente el 5% (como regla general) y es inverosímil que ciertos grupos de pacientes (por ejemplo, los participantes muy enfermos o los muy «buenos») se pierdan específicamente durante el seguimiento en uno de los grupos comparados . En otras palabras, si el impacto potencial de los datos perdidos es insignificante, los datos perdidos pueden ignorarse en el análisis. En caso de duda, se pueden utilizar los análisis de sensibilidad del mejor y peor caso: primero se genera un conjunto de datos del «mejor caso» en el que se asume que todos los participantes perdidos durante el seguimiento en un grupo (denominado grupo 1) han tenido un resultado beneficioso (por ejemplo, no han tenido ningún acontecimiento adverso grave); y todos los que faltan en el otro grupo (grupo 2) han tenido un resultado perjudicial (por ejemplo, han tenido un acontecimiento adverso grave). A continuación, se genera un conjunto de datos en el «peor de los casos», en el que se supone que todos los participantes perdidos durante el seguimiento en el grupo 1 han tenido un resultado perjudicial, y que todos los perdidos durante el seguimiento en el grupo 2 han tenido un resultado beneficioso. Si se utilizan resultados continuos, un «resultado beneficioso» podría ser la media del grupo más 2 desviaciones estándar (o 1 desviación estándar) de la media del grupo, y un «resultado perjudicial» podría ser la media del grupo menos 2 desviaciones estándar (o 1 desviación estándar) de la media del grupo. Para los datos dicotomizados, estos análisis de sensibilidad del mejor-peor y del peor-mejor caso mostrarán entonces el rango de incertidumbre debido a los datos que faltan, y si este rango no da resultados cualitativamente contradictorios, entonces los datos que faltan pueden ser ignorados. Para los datos continuos, la imputación con 2 SD representará un posible rango de incertidumbre dado el 95% de los datos observados (si se distribuyen normalmente).
- b)
Si sólo la variable dependiente tiene valores perdidos y no se identifican las variables auxiliares (variables no incluidas en el análisis de regresión, pero correlacionadas con una variable con valores perdidos y/o relacionadas con su ausencia), el análisis de caso completo puede utilizarse como análisis primario y no deben utilizarse métodos específicos para tratar los datos perdidos. No se obtendrá información adicional, por ejemplo, utilizando la imputación múltiple, pero los errores estándar pueden aumentar debido a la incertidumbre introducida por la imputación múltiple.
- c)
Como se ha mencionado anteriormente (véase Métodos para tratar los datos que faltan), también sería válido simplemente realizar el análisis de casos completos si es relativamente seguro que los datos son MCAR (véase Introducción). Es relativamente raro que se tenga la certeza de que los datos son MCAR. Es posible poner a prueba la hipótesis de que los datos son MCAR con la prueba de Little, pero puede ser imprudente basarse en pruebas que resultaron ser insignificantes. Por lo tanto, si hay una duda razonable sobre si los datos son MCAR, incluso si la prueba de Little es insignificante (no rechaza la hipótesis nula de que los datos son MCAR), entonces no se debe asumir que los datos son MCAR.
¿Son demasiado grandes las proporciones de datos que faltan?
Si faltan grandes proporciones de datos se debe considerar sólo informar de los resultados del análisis completo del caso y luego discutir claramente las limitaciones interpretativas resultantes de los resultados del ensayo. Si se utilizan imputaciones múltiples u otros métodos para manejar los datos faltantes, podría indicarse que los resultados del ensayo son confirmatorios, lo que no es así si la falta de datos es considerable. Si las proporciones de datos faltantes son muy grandes (por ejemplo, más del 40%) en variables importantes, entonces los resultados del ensayo sólo pueden considerarse como resultados generadores de hipótesis . Una rara excepción sería si el mecanismo subyacente detrás de los datos que faltan puede describirse como MCAR (véase el párrafo anterior).
¿Parecen inverosímiles tanto la hipótesis MCAR como la MAR?
Si la hipótesis MAR parece inverosímil basándose en las características de los datos que faltan, entonces los resultados del ensayo correrán el riesgo de estar sesgados debido al «sesgo de datos de resultados incompletos» y ningún método estadístico puede tener en cuenta con certeza este sesgo potencial . La validez de los métodos utilizados para tratar los datos MNAR requiere ciertas suposiciones que no pueden probarse a partir de los datos observados. Los análisis de sensibilidad del mejor-peor y del peor-mejor caso pueden mostrar todo el rango teórico de incertidumbre y las conclusiones deberían estar relacionadas con este rango de incertidumbre. Las limitaciones de los análisis deben ser discutidas y consideradas a fondo.
¿La variable de resultado con valores perdidos es continua y el modelo analítico es complicado (por ejemplo, con interacciones)?
En esta situación, se puede considerar el uso del método de máxima verosimilitud directa para evitar los problemas de compatibilidad del modelo entre el modelo analítico y el modelo de imputación múltiple cuando el primero es más general que el segundo. En general, se pueden utilizar los métodos de máxima verosimilitud directa, pero, por lo que sabemos, los métodos disponibles comercialmente sólo están disponibles para las variables continuas.
Cuándo y cómo utilizar las imputaciones múltiples
Si no se cumple ninguna de las «Razones por las que no se debe utilizar la imputación múltiple para tratar los datos que faltan» mencionadas anteriormente, se podría utilizar la imputación múltiple. En las últimas décadas se han sugerido varios procedimientos en la literatura para tratar los datos que faltan. En la Fig. 1 hemos resumido las consideraciones mencionadas sobre los métodos estadísticos para tratar los datos que faltan.
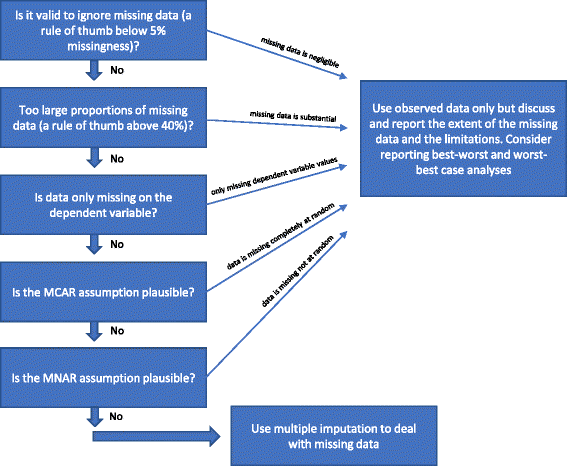
Diagrama de flujo: cuándo debe utilizarse la imputación múltiple para tratar los datos que faltan cuando se analizan los resultados de los ensayos clínicos aleatorios
La imputación múltiple se originó a principios de la década de 1970, y ha ganado una popularidad creciente a lo largo de los años . La imputación múltiple es una técnica estadística basada en la simulación para tratar los datos que faltan . La imputación múltiple consta de tres pasos:
-
Etapa de imputación. Una «imputación» generalmente representa un conjunto de valores plausibles para los datos que faltan – la imputación múltiple representa múltiples conjuntos de valores plausibles . Cuando se utiliza la imputación múltiple, los valores que faltan se identifican y se sustituyen por una muestra aleatoria de imputaciones de valores plausibles (conjuntos de datos completos). Los conjuntos de datos múltiples completados se generan a través de algún modelo de imputación elegido . Tradicionalmente se ha sugerido que cinco conjuntos de datos imputados son suficientes por motivos teóricos, pero parece preferible 50 conjuntos de datos (o más) para reducir la variabilidad del muestreo del proceso de imputación.
-
Paso de análisis de datos completados (estimación). El análisis deseado se realiza por separado para cada conjunto de datos que se genera durante el paso de imputación . Así, por ejemplo, se construyen 50 resultados de análisis.
-
Paso de agrupación. Los resultados obtenidos de cada uno de los análisis de datos completados se combinan en un único resultado de imputación múltiple . No es necesario realizar un meta-análisis ponderado ya que se considera que todos los resultados de los 50 análisis tienen el mismo peso estadístico.
Es de gran importancia que haya compatibilidad entre el modelo de imputación y el modelo de análisis o que el modelo de imputación sea más general que el modelo de análisis (por ejemplo, que el modelo de imputación incluya más covariables independientes que el modelo de análisis) . Por ejemplo, si el modelo de análisis tiene interacciones significativas, entonces el modelo de imputación debería incluirlas también , si el modelo de análisis utiliza una versión transformada de una variable entonces el modelo de imputación debería utilizar la misma transformación , etc.
Diferentes tipos de imputación múltiple
Existen diferentes tipos de métodos de imputación múltiple. Los presentaremos según sus grados crecientes de complejidad: 1) análisis de regresión de un solo valor; 2) imputación monótona; 3) ecuaciones encadenadas o el método Markov chain Monte Carlo (MCMC). En los siguientes párrafos describiremos estos diferentes métodos de imputación múltiple y cómo elegir entre ellos.
Un análisis de regresión de una sola variable incluye una variable dependiente y las variables de estratificación utilizadas en la aleatorización. Las variables de estratificación suelen incluir un indicador de centro si el ensayo es multicéntrico y, por lo general, una o más variables de ajuste con información pronóstica que están correlacionadas con el resultado. Cuando se utiliza una variable dependiente continua, también puede incluirse un valor de referencia de la variable dependiente. Como se menciona en «Razones por las que no deben utilizarse métodos estadísticos para tratar los datos que faltan», si sólo la variable dependiente tiene valores que faltan y no se identifican variables auxiliares, debe realizarse un análisis completo del caso y no deben utilizarse métodos específicos para tratar los datos que faltan. Si se han identificado las variables auxiliares, se puede realizar una imputación de una sola variable. Si hay omisiones significativas en la variable de base de una variable continua, un análisis de caso completo puede proporcionar resultados sesgados . Por lo tanto, en todos los casos, se lleva a cabo una imputación de variable única (con o sin inclusión de variables auxiliares, según proceda) si sólo falta la variable de referencia.
Si faltan tanto la variable dependiente como la de referencia y la falta es monótona, se realiza una imputación monótona. Supongamos una matriz de datos en la que los pacientes están representados por filas y las variables por columnas. Se dice que la omisión de dicha matriz de datos es monótona si sus columnas pueden reordenarse de tal manera que para cualquier paciente (a) si falta un valor también faltan todos los valores a la derecha de su posición, y (b) si se observa un valor también se observan todos los valores a la izquierda de este valor. Si la falta es monótona, el método de imputación múltiple también es relativamente sencillo, incluso si más de una variable tiene valores perdidos. En este caso, es relativamente sencillo imputar los datos que faltan utilizando la imputación por regresión secuencial, en la que los valores que faltan se imputan para cada variable a la vez. Muchos paquetes estadísticos (por ejemplo, STATA) pueden analizar si la falta es monótona o no.
Si la falta no es monótona, se realiza una imputación múltiple utilizando las ecuaciones encadenadas o el método MCMC. Las variables auxiliares se incluyen en el modelo si están disponibles. Hemos resumido cómo elegir entre los diferentes métodos de imputación múltiple en la Fig. 2.
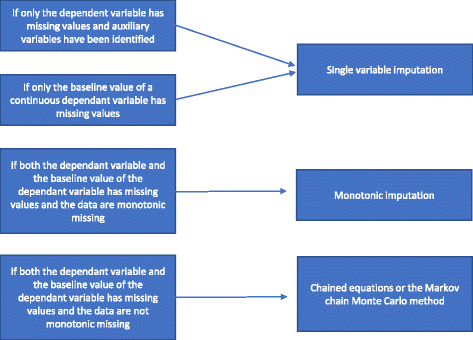
Diagrama de flujo de la imputación múltiple
Máxima Verosimilitud de Información Completa
La máxima Verosimilitud de Información Completa es un método alternativo para tratar los datos que faltan. El principio de la estimación de máxima verosimilitud consiste en estimar los parámetros de la distribución conjunta del resultado (Y) y las covariables (X1,…, Xk) que, de ser ciertos, maximizarían la probabilidad de observar los valores que de hecho observamos . Si faltan valores en un determinado paciente, podemos obtener la probabilidad sumando la probabilidad habitual sobre todos los posibles valores de los datos que faltan, siempre que el mecanismo de los datos que faltan sea ignorable. Este método se denomina máxima verosimilitud con información completa.
La máxima verosimilitud con información completa tiene tanto puntos fuertes como limitaciones en comparación con la imputación múltiple.
Puntos fuertes de la máxima verosimilitud con información completa en comparación con la imputación múltiple
- 1)
Es más simple de implementar, es decir. no es necesario pasar por diferentes pasos como cuando se utiliza la imputación múltiple.
- 2)
A diferencia de la imputación múltiple, la máxima verosimilitud con información completa no tiene problemas potenciales de incompatibilidad entre el modelo de imputación y el modelo de análisis (véase «Imputación múltiple»). La validez de los resultados de la imputación múltiple será cuestionable si existe una incompatibilidad entre el modelo de imputación y el modelo de análisis, o si el modelo de imputación es menos general que el modelo de análisis.
- 3)
Cuando se utiliza la imputación múltiple, todos los valores que faltan en cada conjunto de datos generado (paso de imputación) se sustituyen por una muestra aleatoria de valores plausibles . Por lo tanto, a menos que se especifique ‘una semilla aleatoria’, cada vez que se realice un análisis de imputación múltiple se mostrarán resultados diferentes . Los análisis que utilizan la máxima verosimilitud de la información completa en el mismo conjunto de datos producirán los mismos resultados cada vez que se realice el análisis y, por lo tanto, los resultados no dependen de una semilla de números aleatorios. Sin embargo, si el valor de la semilla aleatoria se define en el plan de análisis estadístico, este problema puede resolverse.
Limitaciones de la máxima verosimilitud de información completa en comparación con la imputación múltiple
Las limitaciones de la utilización de la máxima verosimilitud de información completa en comparación con el uso de la imputación múltiple, es que el uso de la máxima verosimilitud de información completa sólo es posible utilizando un software especialmente diseñado . Se han desarrollado programas informáticos preliminares diseñados, pero la mayoría de ellos carecen de las características de los programas estadísticos diseñados comercialmente (por ejemplo, STATA, SAS o SPSS). En STATA (mediante el comando SEM) y en SAS (mediante el comando PROC CALIS), es posible utilizar la máxima verosimilitud con información completa, pero sólo cuando se utilizan variables dependientes (de resultado) continuas. Para la regresión logística y la regresión de Cox, el único paquete comercial que proporciona información completa de máxima verosimilitud para los datos que faltan es Mplus.
Una limitación potencial adicional cuando se utiliza la información completa de máxima verosimilitud es que puede haber un supuesto subyacente de normalidad multivariante. No obstante, las violaciones del supuesto de normalidad multivariante pueden no ser tan importantes, por lo que podría ser aceptable incluir variables independientes binarias en el análisis.
En el archivo adicional 1 hemos incluido un programa (SAS) que produce un conjunto de datos de juguete completo que incluye varios análisis diferentes de estos datos. La Tabla 1 y la Tabla 2 muestran la salida y cómo los diferentes métodos que manejan los datos perdidos producen diferentes resultados.
Análisis de regresión de los valores del panel
Los datos del panel suelen estar contenidos en un archivo de datos denominado amplio, en el que la primera fila contiene los nombres de las variables, y las filas siguientes (una por cada paciente) contienen los valores correspondientes. El resultado está representado por diferentes variables, una para cada medición planificada y cronometrada del resultado. Para analizar los datos, hay que convertir el archivo en uno de los denominados archivos largos, con un registro por cada medición de resultado planificada, que incluya el valor del resultado, el momento de la medición y una copia de todos los demás valores de las variables, excluyendo los de la variable de resultado. Para conservar las correlaciones dentro del paciente entre las medidas de resultado cronometradas, es una práctica común realizar una imputación múltiple del archivo de datos en su forma amplia, seguida de un análisis del archivo resultante después de haberlo convertido a su forma larga. Se puede utilizar Proc. mixed (SAS 9.4) para el análisis de valores de resultado continuos y proc. glimmix (SAS 9.4) para otros tipos de resultado. Debido a que estos procedimientos aplican el método directo de máxima verosimilitud en los datos de resultados, pero ignoran los casos con valores de covariable faltantes, los procedimientos pueden utilizarse directamente cuando sólo faltan los valores de la variable dependiente y no se dispone de buenas variables auxiliares. De lo contrario, el proc. mixto o el proc. glimmix (el que sea apropiado) debe utilizarse después de una imputación múltiple. Evidentemente, puede ser posible un enfoque correspondiente utilizando otros paquetes estadísticos.
Análisis de sensibilidad
Los análisis de sensibilidad pueden definirse como un conjunto de análisis en los que los datos se manejan de forma diferente en comparación con el análisis primario. Los análisis de sensibilidad pueden mostrar cómo las suposiciones, diferentes de las realizadas en el análisis primario, influyen en los resultados obtenidos. El análisis de sensibilidad debería estar predefinido y descrito en el plan de análisis estadístico, pero los análisis de sensibilidad adicionales post hoc podrían estar justificados y ser válidos. Cuando la influencia potencial de los valores que faltan no está clara, recomendamos los siguientes análisis de sensibilidad:
-
Ya hemos descrito el uso de los análisis de sensibilidad del mejor-peor y del peor-mejor caso para mostrar el rango de incertidumbre debido a los datos que faltan (véase Evaluación de si deben utilizarse métodos para manejar los datos que faltan). Nuestra descripción anterior de los análisis de sensibilidad del mejor-peor y del peor-mejor caso estaba relacionada con los datos que faltan en una variable dependiente dicotómica o continua, pero estos análisis de sensibilidad también pueden utilizarse cuando faltan datos en las variables de estratificación, valores de referencia, etc. La influencia potencial de los datos que faltan debe evaluarse para cada variable por separado, es decir, debe haber un escenario del mejor-peor y del peor-mejor caso para cada variable (variable dependiente, el indicador de resultado y las variables de estratificación) con datos que faltan.
-
Si se decide que, por ejemplo, deben utilizarse imputaciones múltiples, entonces estos resultados deben ser el resultado primario del resultado dado. Cada análisis de regresión primario debe complementarse siempre con un análisis de casos observados (o disponibles) correspondiente.
Cuando se utilizan métodos de efectos mixtos
El uso de un diseño de ensayo multicéntrico será a menudo necesario para reclutar un número suficiente de participantes en el ensayo dentro de un plazo razonable . Un diseño de ensayo multicéntrico también proporciona una mejor base para la posterior generalización de sus resultados . Se ha demostrado que los métodos de análisis más utilizados en los ensayos clínicos aleatorios funcionan bien con un número reducido de centros (analizando resultados dependientes binarios) . Con un número relativamente grande de centros (50 o más), suele ser óptimo utilizar el «centro» como efecto aleatorio y emplear métodos de análisis de efectos mixtos. A menudo también será válido utilizar métodos de análisis de efectos mixtos cuando se analicen datos longitudinales . En algunas circunstancias podría ser válido incluir la covariable de «efecto aleatorio» (por ejemplo, «centro») como covariable de efecto fijo durante el paso de imputación y luego utilizar el análisis de modelo mixto o las ecuaciones de estimación generalizada (GEE) durante el paso de análisis . Sin embargo, la aplicación de un modelo de efectos mixtos (con, por ejemplo, «centro» como efecto aleatorio) implica que la estructura de múltiples capas de los datos debe tenerse en cuenta al modelar la imputación múltiple. Ahora bien, no se dispone directamente de un software comercial para hacerlo. Sin embargo, se puede utilizar el paquete REALCOME, que puede conectarse a STATA. La interfaz exporta los datos con valores perdidos de STATA a REALCOM, donde la imputación se realiza teniendo en cuenta la naturaleza multinivel de los datos y utilizando un método MCMC que incluye variables continuas y, al utilizar un modelo normal latente, también permite un manejo adecuado de los datos discretos. Los conjuntos de datos imputados pueden analizarse mediante el comando «mi estimate:» de STATA, que puede combinarse con la sentencia «mixed» (para un resultado continuo) o la sentencia «meqrlogit» para un resultado binario u ordinal en STATA. Sin embargo, en el análisis de datos de panel, uno puede encontrarse fácilmente con una situación en la que los datos incluyen tres o más niveles, por ejemplo, mediciones dentro del mismo paciente (nivel 1), pacientes dentro de los centros (nivel 2) y centros (nivel 3) . Para no complicarse con un modelo bastante complicado que puede conducir a la falta de convergencia o a errores estándar inestables y para el que no se dispone de software comercial, recomendaríamos tratar el efecto centro como fijo (directamente o tras la fusión de centros pequeños en uno o más centros de tamaño adecuado, mediante un procedimiento que debe prescribirse en el plan de análisis estadístico) o excluir el centro como covariable. Si la aleatorización se ha estratificado por centro, este último enfoque conducirá a un sesgo al alza de los errores estándar que dará lugar a un procedimiento de prueba algo conservador.