¿Cóncavo frente a convexo?

¿Cuál es la diferencia entre cóncavo y convexo?

Si tuviéramos que describir la diferencia entre cóncavo y convexo de la forma más general posible, diríamos que cualquier objeto hueco y con forma de cuenco es cóncavo, mientras que cualquier objeto parecido a un balón de rugby o de fútbol tiene forma convexa. Pero tal vez la razón por la que convexo y cóncavo son tan comúnmente mal utilizados es porque las dos palabras no son tan simples como nos gustaría que fueran.

La mayoría de las fuentes gramaticales insisten en que el uso de la mnemotecnia es posible para descifrar convexo y cóncavo a través de la palabra cueva. Mientras que la noción de asociar lo cóncavo con el suceso de que algo se «cueva» ayuda a aprender sobre las características de la superficie, es confuso relacionar esta idea hacia temas que implican gráficos.

Para entender en qué se diferencian lo cóncavo y lo convexo, necesitamos aprender cómo se utiliza cada término en la capacidad de las matemáticas, los espejos, las lentes y, finalmente, dentro de la escritura creativa. Una vez que hayas decidido en qué contexto te gustaría utilizar palabras como cóncavo y convexo, aprender sobre sus aspectos técnicos te permitirá tener más confianza a la hora de utilizarlas en el discurso cotidiano.

¿Qué significa cóncavo?

Cóncavo se utiliza como adjetivo o sustantivo para describir la forma de un objeto o superficie que está curvada hacia dentro o ahuecada como un cuenco. Ejemplos de cóncavo en una oración incluyen,

«Sacó el helado del recipiente, dejando una huella cóncava»

Según The Oxford Dictionary of Word Histories, la palabra cóncavo proviene del inglés medio tardío. Cóncavo y concavidad dan lugar al término latino concavus (con- y cavus), que se traduce como ‘junto’ y ‘hueco’ («Concave», 110).

Los sinónimos de cóncavo incluyen:

Dentada, deprimida, abombada, hueca, dentada, empotrada y hundida.

Los antónimos de cóncavo incluyen:

Bombear, abombardear, sobresalir, sobresalir, protuberante.

¿Qué significa convexo?

La palabra convexo, o convexidad, es un adjetivo que describe un objeto o superficie redondeada o curva. En lo que respecta a los objetos, la superficie central de un objeto convexo es más ancha que su esquina exterior. Ejemplos de convexo en una oración incluyen,

«Me caí en la hiedra venenosa y ahora tengo protuberancias rojas y convexas por toda la piel».

Sinónimos de convexo incluyen:

Arqueado, doblado, abultado, levantado.

Los antónimos de convexo incluyen:

Deprimido, hundido.

Funciones cóncavas vs convexas

Una función convexa representa una línea continua en una gráfica donde el punto medio, o entero medio de un dominio, no excede la media del intervalo. Una función cóncava es exactamente lo contrario de una función convexa porque, para que f(x) sea cóncava, f(x) debe ser negativa. Para que las diferencias queden más claras, he aquí un rápido repaso de cómo se comparan los términos:

Cóncava hacia arriba = convexa = convexa hacia abajo

Cóncava hacia abajo = cóncava = convexa hacia arriba

La diferencia entre las funciones cóncavas y convexas se muestra más claramente si observamos una gráfica. Observa cómo la función convexa se abre hacia arriba, mientras que la función cóncava se abre hacia abajo.

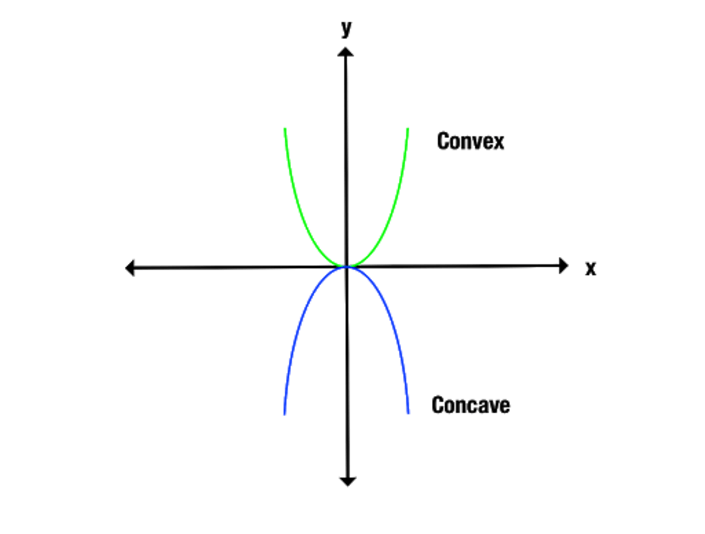
Otra forma de identificar las funciones cóncavas y convexas es conectar los puntos de la gráfica a lo largo del eje x. Una función cóncava sólo conecta líneas por debajo de la gráfica, mientras que una función convexa sólo produce líneas por encima de la gráfica.

Podemos utilizar adicionalmente el cálculo para descifrar si una función es convexa o cóncava. Si la segunda derivada de f(x) es mayor que cero, entonces la función es convexa. Pero si la segunda derivada de f(x) es menor que cero, la función es cóncava.

Polígonos convexos vs. cóncavos

No te asustes, pero las palabras convexo y cóncavo también se utilizan para la geometría. Las formas convexas y cóncavas se discuten más a menudo en referencia a los polígonos, que son formas con un mínimo de tres lados y ángulos.

Los polígonos regulares existen con lados y ángulos iguales, pero los polígonos convexos y cóncavos son un poco más complicados. Los polígonos convexos contienen ángulos interiores que son menores de 180 grados, mientras que los polígonos cóncavos contienen uno o más ángulos interiores que son mayores de 180 grados.

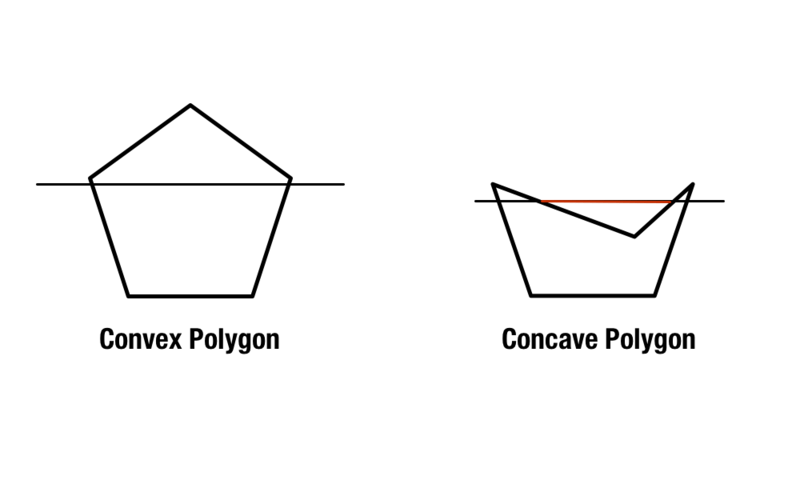
Un segundo método para identificar los polígonos cóncavos y convexos es trazar dos líneas diagonales a través de la forma, partiendo de las esquinas de la misma. Si todas las líneas existen dentro de la forma, ésta es convexa. Si hay al menos una línea que cruza fuera de la forma, es cóncava.

Espejos cóncavos vs. convexos

Las palabras cóncavo y convexo se utilizan comúnmente al hablar de objetos ópticos, como espejos y lentes. Cualquier superficie convexa sobresale hacia fuera, como una burbuja, lo que da el efecto de amplitud. Los espejos convexos se encuentran habitualmente en los aparcamientos, donde los conductores necesitan una visión amplia en las esquinas o en los posibles puntos ciegos.

En cambio, un espejo cóncavo está curvado hacia dentro y produce un reflejo ampliado al revés. Como ha demostrado la Escuela de Física de la Universidad de Gales del Sur, cualquiera que tenga una cuchara brillante puede comprobar esta observación mirando su reflejo en la cuchara. En la superficie cóncava de la cuchara, por donde se coge la comida, su reflejo se distorsiona de forma estrecha, y aparecerá al revés. Pero si le das la vuelta a la cuchara hacia el lado convexo, tu reflejo aparecerá erguido y más pequeño.

Los reflejos varían tanto entre superficies convexas y cóncavas porque, independientemente de que la superficie se curve hacia fuera o hacia dentro, el propio espejo forma parte de una esfera. Como la superficie de una esfera no es plana, la luz reflejada en su superficie recorrerá diferentes distancias antes de entrar en contacto con el espejo.

Dependiendo de la zona de la superficie con la que entre en contacto la luz, un rayo de luz puede reflejarse en superficies cercanas para producir un área de visibilidad más focalizada. Por eso, al mirar la superficie interior de una cuchara, es posible que sólo se vea el reflejo de lo que está más cerca de la superficie de la cuchara… aunque siga pareciendo más pequeña. Además, si se coloca el dedo dentro de la cuchara, la superficie del espejo puede producir dos o tres reflejos diferentes al mismo tiempo.

Lentes cóncavas frente a lentes convexas

Las lentes cóncavas y convexas existen en objetos cotidianos como gafas, lentillas, prismáticos y telescopios. De forma similar a la ciencia que subyace a la reflexión de la luz en los espejos convexos y cóncavos, también existen patrones de cómo la luz pasa a través de las lentes cóncavas y convexas para producir una imagen visible.

Lentes convexas

Según la Academia Manocha, las lentes convexas se llaman lentes convergentes por su capacidad de producir imágenes disminuidas, magnificadas o introvertidas. La precisión con la que aparece una imagen a través de la lente convexa depende de lo cerca que esté el objeto del punto focal de la lente. Para cualquier lente convexa, hay puntos focales simétricos a cada lado de la lente.

La precisión con la que se produce un objeto a través de una lente convexa se predice con tres principios:

Principio 1: Todo rayo de luz que atraviesa una lente convexa es paralelo al eje principal, que es una línea central que pasa por el centro absoluto de una lente esférica. Una vez que la luz entra en contacto con la lente, la luz se refracta y pasa por el punto focal del otro lado. Los rayos de luz que pasan paralelos al eje principal se desplazan por encima del objeto que está delante de la lente.

Principio 2: Cualquier rayo de luz que pase por el centro de una lente convexa continuará en línea recta por el otro lado.
Principio 3: Cualquier rayo de luz que pase por un punto focal en el mismo lado que el objeto se refractará al entrar en contacto con la lente y se volverá paralelo al eje principal en el otro lado.

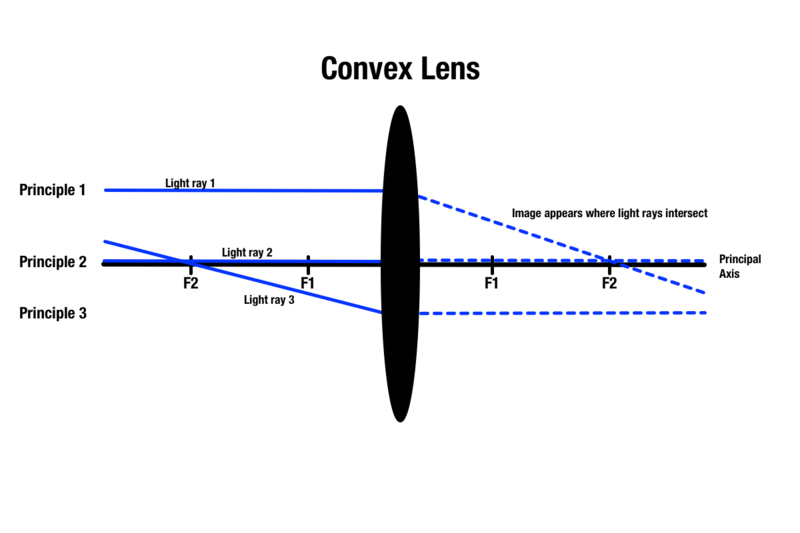
Aunque hay tres principios para predecir la calidad de la imagen a través de una lente convexa, sólo dos principios pueden aplicarse a un objeto mientras se dibuja un diagrama de rayos. Cualquiera de los dos principios producirá una intersección de luz al otro lado de la lente, que indicará la zona donde aparece la imagen del objeto.

Cuanto más lejos esté un objeto de una lente convexa, más pequeña será la imagen en el otro lado, y cuanto más cerca esté un objeto de la lente convexa, más grande aparecerá. Un objeto situado más allá del punto focal más cercano produce una imagen más grande detrás del objeto. Como señala la Academia Manocha, este tipo de aumento de lente se utiliza para herramientas ópticas como las lupas.

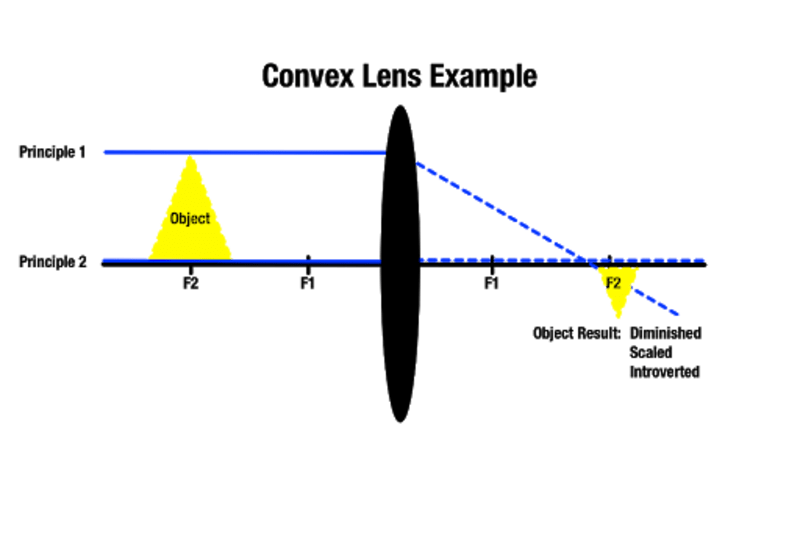
En función del punto focal en el que se encuentre un objeto, es posible producir una imagen de tamaño aproximado. También es posible crear imágenes reales que no son visibles si los rayos de luz que pasan nunca se cruzan porque son paralelos en el otro lado. En este caso, la imagen producida existe a una distancia infinita.

Lentes cóncavas

Cualquier lente cóncava tendrá un diámetro más grueso, y un centro más fino ya que una lente cóncava está curvada hacia dentro. La forma de las lentes cóncavas permite que la luz se disperse una vez que entra en contacto con la lente, lo que permite que los objetos virtuales parezcan más pequeños. La capacidad de la lente cóncava para dispersar la luz la convierte en una lente ideal para herramientas como las linternas, en las que una fuente de luz central puede utilizarse en una superficie más amplia.

Las lentes cóncavas producen imágenes con tres principios similares a las lentes convexas:

Principio 1: Cualquier rayo de luz que se desplace por encima del objeto y sea paralelo al eje principal se refractará al entrar en contacto con la lente y aparecerá como si procediera de la dirección del punto focal más cercano.

Principio 2: Cualquier rayo de luz que pase por el centro de la lente cóncava pasará sin refracción.
Principio 3: Cualquier rayo de luz dirigido hacia un punto focal en el otro lado de la lente cóncava se refractará y se convertirá en paralelo al eje principal.

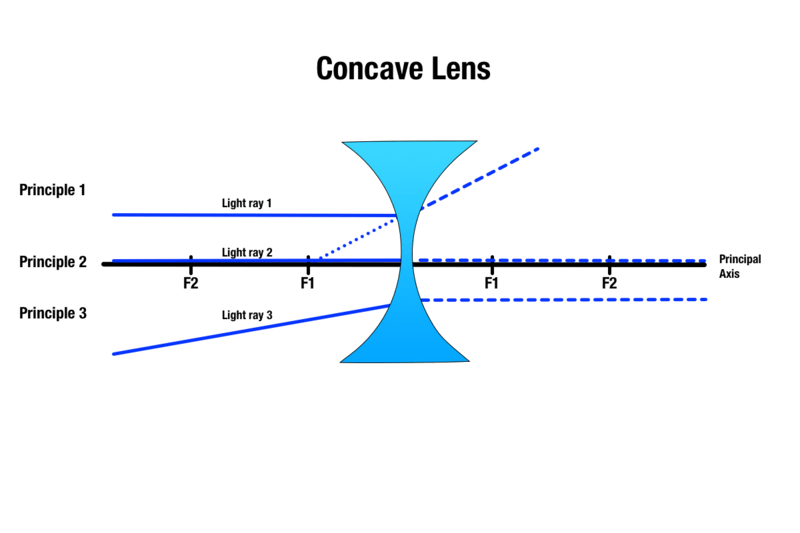
Aunque el tamaño de la imagen del objeto variará dependiendo de la distancia del objeto a una lente cóncava, la imagen producida es siempre virtual, vertical, más pequeña y aparece en el mismo lado de la lente que el objeto.

Cóncavo vs. convexo en la escritura

Las palabras cóncavo y convexo son opuestas entre sí, y esencialmente describen la forma de los objetos o superficies de la misma manera que contrastamos palabras como:

• Pequeño vs. grande
• Alto vs. bajo
• Esbelto vs. ancho
• Redondo vs. plano

Debido a que cóncavo y convexo son palabras técnicas, usarlas descriptivamente para la prosa puede producir una interpretación más metafórica o abstracta para el público casual. Lo que esto significa es que si los escritores deciden utilizar cóncavo o convexo fuera del ámbito de su uso típico, el escritor debe decidir cuán claro pretende que sea su escrito.

Considere el adjetivo

Un ejemplo destacado del uso de cóncavo o convexo en la literatura es considerar los escritos del autor estadounidense David Foster Wallace (o DFW para abreviar). DFW es famoso por su estilo de escritura complejo y técnico… y sí, usó convexo y cóncavo para describir sustantivos varias veces. Wallace utiliza cóncavo y convexo en los siguientes ejemplos:

«Mi ojo de la mano estaba bien, pero no era ni grande ni rápido, tenía un pecho casi cóncavo y unas muñecas tan finas que podía pulsarlas con el pulgar y el meñique…»

– «Tenis, Trigonometría, Tornados: A Midwestern Boyhood», Harper’s Magazine.

«…ojos de muñeca que se abren con el tirón de una cuerda de corazón, cóncavos donde yo soy convexo.»

– «Orden y flujo en Northampton,» Conjunciones.

El objetivo de utilizar los ejemplos de DFW no es simplemente mostrar cómo los escritores han utilizado convexo o cóncavo fuera del contexto matemático, sino más bien, para que los escritores consideren si el uso de términos técnicos o abstractos es útil para comunicar claramente a su audiencia.
En el primer ejemplo de DFW, el uso de cóncavo tiene sentido porque está describiendo la estructura de algo. Pero, usar cóncavo y convexo para describir sustantivos no objetivos, como sentimientos o pensamientos, tiende a oscurecer el significado de lo que estamos tratando de explicar. El segundo ejemplo de DFW camina por una fina línea al usar convexo y cóncavo porque su uso es tanto literal como metafórico.

FAQ: Términos relacionados

¿Qué es una función?

Una función es la ecuación de una línea en una gráfica. Las funciones son diferentes para cada línea en un gráfico, pero toman la forma general de,

f(x) = x + 1

Con cualquier función de línea, la variable dependiente es típicamente f(x), mientras que cualquier variable desconocida dentro de la función se llama una variable independiente.

¿Qué es el dominio?

El dominio es un conjunto de variables independientes en una gráfica que corresponde a la función de una recta. Los dominios son importantes de entender porque localizan puntos específicos en la gráfica que corresponde a cualquier salida real de una ecuación.

¿Qué es el rango?

El rango de cualquier función representa cualquier valor posible a lo largo del eje x o y en una gráfica que produce un valor válido para la variable dependiente. Todos los enteros mínimos y máximos se identifican sustituyendo las variables del eje x o y.

¿Qué es un intervalo?

Un intervalo es un conjunto de números que representan los enteros de una recta, alias el dominio. Un intervalo cerrado incluye dos puntos finitos de una línea, donde la línea ya no existe fuera del rango de un número entero. Un intervalo abierto es un conjunto de números enteros que no representan el extremo absoluto del dominio de una línea.

¡Ponte a prueba!

Comprueba lo bien que entiendes la diferencia entre convexo y cóncavo con las siguientes preguntas de opción múltiple:

1. Mientras miras una cuchara brillante, notas que tu reflejo está al revés. La superficie de la cuchara es una superficie _________.
   a. Convexa
   b. Espejo
   c. Cóncava
   d. Metálica
2. En términos de funciones gráficas, una función convexa se llama a veces:
   a. Cóncava hacia arriba
   b. Convexa hacia abajo
   c. Cóncava hacia abajo
   d. A y B
3. ¿Cuál de las siguientes no describe una superficie cóncava:
   a. Media esfera hueca
   b. Lente ocular
   c. Tazón de cereales
   d. Hemisferio
4. ¿Cuál de las siguientes no describe una superficie convexa:
   a. El personaje Stewie de Padre de familia
   b. Esfera
   c. Espejo de garaje
   d. Fútbol
5. ¿Cuál de las siguientes formas no puede existir como polígono cóncavo:
   a. Pentágono
   b. Hexágono
   c. Triángulo
   d. Octógono

Respuestas

1. C: Cóncavo
2. D: A y B
3. D: Hemisferio
4. B: Esfera
5. C: Triángulo

Fuentes:

1. Bourne, M. «Dominio y rango de una función». Interactive Mathematics, 4 de enero de 2019.
2. «Cóncavo». Diccionario Merriam-Webster, 2019.
3. «Cóncavo». The Oxford Dictionary of Word Histories, Ed. Chantrell, 2002, p. 110.
4. «Espejos cóncavos y convexos». Academia Manocha, YouTube, 2019.
5. «Lente cóncava: Definición & Usos». Estudio.com, 2019.
6. «Convexo». Diccionario Merriam-Webster, 2019.
7. «Lentes convexos y cóncavos». Academia Manocha, YouTube, 2019.
8. «Matemáticas / Entender los polígonos». Learnhive Inc, 2018.
9. «Reflexión desde un espejo cóncavo». UNSW Physics, YouTube, 2017.
10. Wallace, D.F. «Tenis, trigonometría, tornados: A Midwestern Boyhood». Harper’s Magazine, 1991.
11. Wallace, D.F. «Order and Flux in Northampton». Conjunctions, 1991.
12. Weisstein, Eric W. «Concave Function». MathWorld-A Wolfram Web Resource, n.d.
13. Weisstein, Eric W. «Convex Function.» MathWorld-A Wolfram Web Resource, s.f.

El contador de palabras es una herramienta dinámica en línea que se utiliza para contar palabras, caracteres, oraciones, párrafos y páginas en tiempo real, junto con la revisión ortográfica y gramatical.