El algoritmo de Toom-Cook
Aquí aprendemos una ingeniosa aplicación de un algoritmo de divide y vencerás combinado con álgebra lineal para multiplicar números grandes, rápidamente. Y una introducción a la notación Big-O!
De hecho, este resultado es tan contraintuitivo que el gran matemático Kolmogorov conjeturó que no existía un algoritmo tan rápido.
Parte 0: La multiplicación larga es una multiplicación lenta. (Y una introducción a la notación Big-O)
Todos recordamos haber aprendido a multiplicar en la escuela. De hecho, tengo que confesar algo. Recordad que esta es una zona sin juicios 😉
En el colegio, teníamos «juegos húmedos» cuando llovía demasiado para jugar en el patio. Mientras los otros niños (normales/amantes de la diversión/adjetivo positivo de elección) jugaban y hacían el tonto, yo a veces cogía una hoja de papel y multiplicaba números grandes juntos, sólo por el gusto de hacerlo. El puro placer del cálculo. Incluso teníamos una competición de multiplicación, el «Super 144», en el que teníamos que multiplicar una cuadrícula de 12 por 12 (del 1 al 12) lo más rápido posible. Lo practicaba religiosamente, hasta el punto de que tenía mis propias hojas de práctica preparadas de antemano, que fotocopiaba y utilizaba por turnos. Al final conseguí bajar el tiempo a 2 minutos y 1 segundo, momento en el que se alcanzó mi límite físico de garabatos.
A pesar de esta obsesión por la multiplicación, nunca se me ocurrió que pudiéramos hacerlo mejor. Pasé muchas horas multiplicando, pero nunca intenté mejorar el algoritmo.
Consideremos la multiplicación de 103 por 222.
Calculamos 2 veces 3 veces 1 +2 veces 0 veces 10 + 2 veces 1 veces 100 + 20 veces 3 veces 1 + 20 veces 0 veces 10 + 20 veces 1 veces 100 = 22800
En general, para multiplicar a números de n cifras, se necesitan O(n²) operaciones. La notación ‘big-O’ significa que, si tuviéramos que graficar el número de operaciones en función de n, el término n² es realmente lo que importa. La forma es esencialmente cuadrática.
Hoy vamos a cumplir todos nuestros sueños de la infancia y mejorar este algoritmo. Pero antes. Big-O nos espera.
Big-O
Mira las dos gráficas de abajo

Pregúntale a un matemático, «¿son x² y x²+x^(1/3) lo mismo?», y probablemente vomitará en su taza de café y empezará a llorar, y murmurará algo sobre topología. Al menos, esa fue mi reacción (al principio), y apenas sé nada de topología.
Ok. No son lo mismo. Pero a nuestro ordenador no le importa la topología. Los ordenadores difieren en rendimiento de tantas maneras que ni siquiera puedo describir porque no sé nada de ordenadores.
Pero no tiene sentido afinar una apisonadora. Si dos funciones, para valores grandes de su entrada, crecen en el mismo orden de magnitud, entonces a efectos prácticos eso contiene la mayor parte de la información relevante.
En la gráfica anterior, vemos que las dos funciones se parecen bastante para entradas grandes. Pero igualmente, x² y 2x² son similares – esta última es sólo dos veces más grande que la primera. A x = 100, una es de 10.000 y la otra de 20.000. Eso significa que si podemos calcular una, probablemente podamos calcular la otra. Mientras que una función que crece exponencialmente, digamos 10^x, a x = 100 ya es mucho mayor que el número de átomos del universo. (10¹⁰⁰ >>> 10⁸⁰ que es una estimación, el número de Eddington, sobre el número de átomos en el universo según mi búsqueda en Google*).
*en realidad, usé DuckDuckGo.
Escribir números enteros como polinomios es muy natural y muy poco natural. Escribir 1342 = 1000 + 300 + 40 + 2 es muy natural. Escribir 1342 = x³+3x²+4x + 2, donde x = 10, es ligeramente extraño.
En general, supongamos que queremos multiplicar dos números grandes, escritos en base b, con n dígitos cada uno. Escribimos cada número de n cifras como un polinomio. Si dividimos el número de n dígitos en r trozos, este polinomio tiene n/r términos.
Por ejemplo, dejemos que b = 10, r = 3, y nuestro número es 142.122.912
Podemos convertir esto en
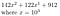
Esto funciona muy bien cuando r = 3 y nuestro número, escrito en base 10, tenía 9 dígitos. Si r no divide perfectamente a n, entonces podemos añadir algunos ceros al principio. De nuevo, esto se ilustra mejor con un ejemplo.
27134 = 27134 + 0*10⁵ = 027134, que representamos como
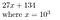
¿Por qué puede ser útil esto? Para encontrar los coeficientes del polinomio P, si el polinomio es de orden N, entonces muestreándolo en N+1 puntos podemos determinar sus coeficientes.
Por ejemplo, si el polinomio x⁵ + 3x³ +4x-2, que es de orden 5, se muestrea en 6 puntos, podemos entonces elaborar el polinomio completo.
Intuitivamente, un polinomio de orden 5 tiene 6 coeficientes: el coeficiente de 1, x, x², x³, x⁴, x⁵. Dados 6 valores y 6 incógnitas, podemos averiguar los valores.
(Si sabes álgebra lineal, puedes tratar las diferentes potencias de x como vectores linealmente independientes, hacer una matriz para representar la información, invertir la matriz, y voilá)
Muestreo de polinomios para determinar los coeficientes (Opcional)
Aquí profundizamos un poco en la lógica que hay detrás del muestreo de un polinomio para deducir sus coeficientes. Siéntase libre de saltar a la siguiente sección.
Lo que demostraremos es que, si dos polinomios de grado N coinciden en N+1 puntos, entonces deben ser iguales. Es decir, N+1 puntos especifican de forma única un polinomio de orden N.
Consideremos un polinomio de orden 2. Este es de la forma P(z) = az² +bz + c. Por el teorema fundamental del álgebra -descarado, plug aquí, pasé varios meses armando una prueba de esto, y luego escribiéndola, aquí- este polinomio puede ser factorizado. Eso significa que podemos escribirlo como A(z-r)(z-w)
Nótese que en z = r, y en z = w, el polinomio evalúa a 0. Decimos que w y r son raíces del polinomio.
Ahora demostramos que P(z) no puede tener más de dos raíces. Supongamos que tiene tres raíces, que llamamos w, r, s. Entonces factorizamos el polinomio. P(z) = A(z-r)(z-w). Entonces P(s) = A(s-r)(s-w). Esto no es igual a 0, ya que al multiplicar números distintos de cero se obtiene un número distinto de cero. Esto es una contradicción porque nuestra suposición original era que s era una raíz del polinomio P.
Este argumento se puede aplicar a un polinomio de orden N de forma esencialmente idéntica.
Ahora, supongamos que dos polinomios P y Q de orden N coinciden en N+1 puntos. Entonces, si son diferentes, P-Q es un polinomio de orden N que es 0 en N+1 puntos. Por lo anterior, esto es imposible, ya que un polinomio de orden N tiene a lo sumo N raíces. Por tanto, nuestra suposición debe haber sido errónea, y si P y Q coinciden en N+1 puntos son el mismo polinomio.
Ver para creer: Un ejemplo trabajado
Veamos un número realmente enorme al que llamamos p. En base 10, p tiene 24 dígitos (n=24), y lo dividiremos en 4 trozos (r=4). n/r = 24/4 = 6
p = 292,103,243,859,143,157,364,152.
Y dejemos que el polinomio que lo representa se llame P,
P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152
con P(10⁶) = p.
Como el grado de este polinomio es 3, podemos calcular todos los coeficientes a partir del muestreo en 4 lugares. Vamos a ver qué pasa cuando lo muestreamos en algunos puntos.
- P(0) = 364,152
- P(1) = 1,043,271
- P(-1) = 172,751
- P(2) = 3,962,726
Lo que llama la atención es que todos tienen 6 ó 7 dígitos. Eso en comparación con los 24 dígitos que se encuentran originalmente en p.
Multipliquemos p por q. Sea q = 124,153,913,241,143,634,899,130, y
Q(x) = 124,153 x³ + 913,241 x²+143,634 x + 899,130
Calcular t=pq podría ser horrible. Pero en lugar de hacerlo directamente, intentamos calcular la representación polinómica de t, que etiquetamos como T. Como P es un polinomio de orden r-1=3, y Q es un polinomio de orden r-1 = 3, T es un polinomio de orden 2r-2 = 6.
T(10⁶) = t = pq
T(10⁶) = P(10⁶)Q(10⁶)
El truco es que vamos a calcular los coeficientes de T, en lugar de multiplicar directamente p y q. Entonces, calcular T(1⁰⁶) es fácil, porque para multiplicar por 1⁰⁶ sólo tenemos que pegar 6 ceros por detrás. Sumar todas las partes también es fácil porque la suma es una acción de muy bajo coste para los ordenadores.
Para calcular los coeficientes de T, necesitamos muestrearlo en 2r-1 = 7 puntos, porque es un polinomio de orden 6. Probablemente queramos escoger enteros pequeños, así que elegimos
- T(0)=P(0)Q(0)= 364,152*899,130
- T(1)=P(1)Q(1)= 1,043,271*2,080,158
- T(2)=P(2)Q(2)= 3,962,726*5,832,586
- T(-1)=P(-1)Q(-1)= 172751*1544584
- T(-2)=P(-2)Q(-2)= -1.283.550*3.271,602
- T(3)=P(-3)Q(-3)= -5.757.369*5.335.266
Note el tamaño de P(-3), Q(-3), P(2), Q(2) etc… Todos estos son números con aproximadamente n/r = 24/4 = 6 dígitos. Algunos tienen 6 dígitos, otros 7. A medida que n se hace más grande, esta aproximación es cada vez más razonable.
Hasta ahora hemos reducido el problema a los siguientes pasos, o algoritmo:
(1) Primero calculamos P(0), Q(0), P(1), Q(1), etc (acción de bajo coste)
(2) Para obtener nuestros 2r-1= 7 valores de T(x), ahora debemos multiplicar 2r-1 números de tamaño aproximado n/r dígitos. Es decir, debemos calcular P(0)Q(0), P(1)Q(1), P(-1)Q(-1), etc. (Acción de alto coste)
(3) Reconstruir T(x) a partir de nuestros puntos de datos. (Acción de bajo coste: pero entrará en consideración más adelante).
(4) Con nuestro T(x) reconstruido, evaluar T(10⁶) en este caso
Esto nos lleva agradablemente a un análisis del tiempo de ejecución de este enfoque.
Tiempo de ejecución
A partir de lo anterior, descubrimos que, ignorando temporalmente las acciones de bajo coste (1) y (3), el coste de multiplicar dos números de n cifras con el algoritmo de Toom obedecerá a:
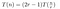
Esto es lo que vimos en el ejemplo trabajado. Multiplicar cada P(0)Q(0), P(1)Q(1), etc cuesta T(n/r) porque estamos multiplicando dos números de longitud aproximada n/r. Tenemos que hacer esto 2r-1 veces, ya que queremos muestrear T(x) -siendo un polinomio de orden 2r-2- en 2r-1 lugares.
¿Qué tan rápido es esto? Podemos resolver este tipo de ecuación de forma explícita.

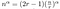
Todo lo que queda ahora es algo de álgebra desordenada
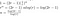
Como hubo algunos otros costos del proceso de multiplicación de la matriz (‘reensamblaje’), y de la adición, no podemos decir realmente que nuestra solución es el tiempo de ejecución exacto, así que en su lugar concluimos que hemos encontrado el big-O del tiempo de ejecución
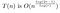
Optimizando r
Este tiempo de ejecución todavía depende de r. Si fijamos r, habremos terminado. Pero nuestra curiosidad aún no está satisfecha.
A medida que n se hace grande, queremos encontrar un valor aproximadamente óptimo para nuestra elección de r. Es decir, queremos elegir un valor de r que cambie para diferentes valores de n.
La clave aquí es que, al variar r, tenemos que prestar cierta atención al coste de reensamblaje: la matriz que realiza esta operación tiene un coste de O(r²). Cuando r era fijo, no teníamos que fijarnos en eso, porque a medida que n crecía con r fijo, eran los términos que involucraban a n los que determinaban el crecimiento de la cantidad de computación requerida. Como nuestra elección óptima de r será mayor a medida que n sea mayor, ya no podemos ignorar esto.
Esta distinción es crucial. Inicialmente, nuestro análisis elegía un valor de r, tal vez 3, tal vez 3.000 millones, y luego observaba el tamaño de big-O a medida que n crecía arbitrariamente. Ahora, observamos el comportamiento a medida que n crece arbitrariamente y r crece con n a un ritmo que determinamos. Este cambio de perspectiva considera a O(r²) como una variable, mientras que cuando r se mantenía fija, O(r²) era una constante, aunque una que no conocíamos.
Así que actualizamos nuestro análisis de antes:
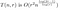
donde O(r²) representa el coste de la matriz de reensamblaje. Ahora queremos elegir un valor de r para cada valor de n, que minimice aproximadamente esta expresión. Para minimizar, primero intentamos diferenciar con respecto a r. Esto da la expresión de aspecto algo atroz

Normalmente, para encontrar el punto mínimo, establecemos la derivada igual a 0. Pero esta expresión no tiene un buen mínimo. En su lugar, encontramos una solución «suficientemente buena». Utilizamos r = r^(sqrt(logN)) como nuestro valor estimado. Gráficamente, esto está bastante cerca del mínimo. (En el diagrama de abajo, el factor 1/1000 está ahí para hacer visible el gráfico a una escala razonable)
El gráfico de abajo muestra nuestra función para T(N), escalada por una constante, en rojo. La línea verde está en x = 2^sqrt(logN) que era nuestro valor estimado. ‘x’ toma el lugar de ‘r’, y en cada una de las tres imágenes se utiliza un valor diferente de N.



Esto me convence bastante de que nuestra elección fue acertada. Con esta elección de r, podemos enchufarla y ver cómo el big-O final de nuestro algoritmo:

donde simplemente enchufamos nuestro valor para r, y usamos una aproximación para log(2r-1)/log(r) que es muy precisa para valores grandes de r.
¿Cuánta mejora?
Quizás el no haber detectado este algoritmo cuando era un chiquillo haciendo multiplicaciones fue razonable. En el gráfico siguiente, doy el coeficiente de nuestra función big-O a 10 (para fines de demostración) y lo divido por x² (ya que el enfoque original de la multiplicación era O(n²)). Si la línea roja tiende a 0, eso mostraría que nuestro nuevo tiempo de ejecución es asintóticamente mejor que O(n²).
Y de hecho, aunque la forma de la función muestra que nuestro enfoque es eventualmente más rápido, y eventualmente es mucho más rápido, ¡tenemos que esperar hasta que tengamos números de casi 400 dígitos de largo para que este sea el caso! Incluso si el coeficiente fuera sólo 5, los números tendrían que tener unos 50 dígitos para ver una mejora en la velocidad.

¡Para mi yo de 10 años, multiplicar números de 400 dígitos sería un poco exagerado! Mantener un registro de las diversas llamadas recursivas de mi función también sería algo desalentador. Pero para un ordenador que hace una tarea en la IA o en la física, este es un problema común!
¿Qué tan profundo es este resultado?
Lo que me gusta de esta técnica es que no es ciencia espacial. No es la matemática más alucinante que se haya descubierto. En retrospectiva, ¡quizás parezca obvio!
Sin embargo, esta es la brillantez y la belleza de las matemáticas. Leí que Kolmogorov conjeturó en un seminario que la multiplicación era fundamentalmente O(n²). Kolmogorov básicamente inventó gran parte de la teoría de la probabilidad y el análisis modernos. Fue uno de los grandes matemáticos del siglo XX. Sin embargo, en lo que respecta a este campo no relacionado, resultó que había todo un corpus de conocimiento esperando a ser descubierto, ¡situado delante de sus narices y de las de todos los demás!
De hecho, los algoritmos de «Divide y vencerás» nos vienen a la mente muy rápidamente hoy en día, ya que son muy utilizados. Pero son un producto de la revolución informática, en el sentido de que sólo con la enorme potencia de cálculo las mentes humanas se han centrado específicamente en la velocidad de cálculo como un área de las matemáticas digna de ser estudiada por derecho propio.
Esta es la razón por la que los matemáticos no están simplemente dispuestos a aceptar que la Hipótesis de Riemann es cierta sólo porque parece que podría serlo, o que P no es igual a NP sólo porque eso parece lo más probable. El maravilloso mundo de las matemáticas siempre conserva la capacidad de confundir nuestras expectativas.
De hecho, se pueden encontrar formas aún más rápidas de multiplicar. Las mejores aproximaciones actuales utilizan transformadas de fourier rápidas. Pero eso lo dejaré para otro día 🙂
Hazme saber tu opinión abajo. Estoy recién en Twitter como ethan_the_mathmo, puedes seguirme aquí.
Me encontré con este problema en un maravilloso libro que estoy usando llamado ‘The Nature of Computation’ de los físicos Moore y Mertens, donde uno de los problemas te guía a través del análisis del algoritmo de Toom.