Cómo ayudar a los alumnos que tienen dificultades con los problemas de palabras

«Conocen las matemáticas. Simplemente no pueden hacer los problemas de palabras. Es su comprensión lectora»

La señora Hartwell estaba explicando por qué sus alumnos habían tenido problemas en los exámenes estatales. Conocía a sus alumnos y había realizado una amplia evaluación. Estaba segura de que sus dificultades eran un problema de alfabetización.

«No entiendo por qué hacen la lectura tan difícil. Los niños ya hacen un examen de lengua y literatura».

Me habían asignado a la Sra. Hartwell (y a otros de su escuela) como parte de un programa de la ciudad de Nueva York para mejorar el rendimiento en matemáticas. El objetivo era llevar las matemáticas conceptuales a las escuelas de «nivel 1». Las escuelas de nivel 1 eran las que estaban a la cabeza de la ciudad en tres áreas. Los ingresos más bajos, las puntuaciones más bajas en los exámenes y el mayor porcentaje de estudiantes de color.

Había escuchado la explicación de la «alfabetización» de otros profesores del programa. Y tenía sentido. Si los alumnos conocían las matemáticas, ¿por qué si no tenían problemas en el examen, que tenía muchos problemas de palabras?

Pero había una trampa. En los últimos tres años, el nivel de alfabetización había pasado del 30% al 40% en toda la ciudad. Durante el mismo período, las puntuaciones en matemáticas se han mantenido casi sin cambios.

Si se tratara de un problema de lectura, los aumentos en las puntuaciones de lectura deberían desencadenar un crecimiento explosivo en matemáticas. Además, el lenguaje de los problemas de palabras no parecía lo suficientemente complicado como para causar problemas.

El siguiente período, estaba programado para visitar la clase de la Sra. Hartwell. Ella había planeado una lección sobre problemas de palabras, así que pude ver el problema de primera mano.

Se sentaron los estudiantes en mesas redondas, y ella se puso al frente. Tanto ella como sus alumnos tenían pizarras blancas de mano.

Ellos abrieron sus libros de texto en la página 47 y ella leyó un problema de palabras en voz alta. «Sarah tiene 40 libras de zanahorias para sus caballos. Si tiene 100 caballos, ¿cuántas libras recibe cada caballo?».

«Bien clase, ella tiene 40 libras que le dará a cada caballo. Entonces, ¿qué operación necesitamos?»

Señaló un gráfico de anclaje que enumeraba las ‘palabras clave’ para cada operación. ‘Cada’ estaba al principio de la lista de divisiones.

«¡División!», respondió la clase.

«Bien. Entonces, ¿cómo dividimos un número pequeño entre un número grande?»

La clase se quedó callada. La señora Hartwell dibujó un vinculum (casa de división larga) en su pizarra. Los alumnos copiaron mientras ella ponía 40 debajo de la casa y 100 fuera.

«Ahora 100 no cabe en 40, así que tenemos que añadir un decimal». Cambió 40 por 40,0. «¿Cuántas veces entra 100 en 400?».

Algunos alumnos gritaron «¡Cuatro!»

«Exactamente. Ahora, tenemos que poner también un decimal en nuestro cociente. Nuestra respuesta final es…»

La clase leyó la respuesta, «0,4», en su pizarra.

Asignó un problema similar, y señaló el póster «CUBOS» en la pared. «Recordad rodear los números y marcar las palabras clave con un recuadro».

La profesora circulaba mientras los alumnos trabajaban. Algunos preguntaban dónde poner el decimal. Otros tenían problemas para alinear la parte de la resta de la división larga. Algunos estudiantes trabajaban en parejas, uno hacía el cálculo y el otro copiaba.

Al final de la lección, todos tenían la respuesta correcta en su papel. «¿Ves?» La Sra. Hartwell comentó, «todos saben las matemáticas».

¿Qué fue lo que falló?

Aunque este es un ejemplo extremo, muchos de los errores que cometió la Sra. Hartwell son en realidad bastante comunes.

El sobreesfuerzo ocurre cuando proporcionamos a los estudiantes demasiado apoyo. Aunque es común que los educadores se enorgullezcan de proporcionar a los estudiantes «todo el apoyo que necesiten», el exceso de andamiaje es diferente.

El término «andamiaje» proviene del trabajo de Lev Vygotsky. Él acuñó el término «Zona de Desarrollo Próximo». La ZPD incluye cosas que están justo fuera del alcance de un alumno. No pueden hacerlo por sí mismos, pero pueden hacerlo con apoyo. Mediante el «andamiaje», podemos trasladar estas habilidades al conjunto de habilidades principales del alumno.

Lo que a menudo se pasa por alto es que el andamiaje sólo se aplica a las habilidades que ya están en la ZPD del alumno. Hay toda una serie de destrezas que están fuera del alcance del alumno. Cuando tratamos de andamiar estas destrezas, hacemos más daño que bien.

Un problema del exceso de andamiaje es que los estudiantes nunca interiorizan las destrezas que se pretenden. Cuando ayudamos a un alumno con algo fuera de su ZPD, siempre necesitará nuestra ayuda. Al menos hasta que identifiquemos las habilidades intermedias que están en su ZPD.

Otro problema es que el exceso de andamiaje nos da una falsa sensación de éxito. En este caso, la Sra. Hartwell creía que sus alumnos podían «hacer las matemáticas» en el problema de palabras. En realidad, sólo estaban imitando sus acciones. No había ninguna razón para creer que podrían encontrar una solución similar por sí mismos.

También eliminó todo el proceso de «formulación» del proceso de resolución de problemas. Muchos educadores piensan que la comprensión y la formulación son lo mismo, pero la formulación es una competencia matemática independiente.

Y puede ser el ingrediente que falta en la forma en que actualmente se enseñan los problemas de palabras.

Recursos para el aula y aprendizaje profesional

Formulación: La clave del éxito con los problemas de palabras

Formular problemas de palabras implica comprenderlos. Pero va más allá. La formulación se parece más a la traducción que a la comprensión.

Cuando un alumno lee un problema de palabras, primero tiene que convertir las letras en sonidos (descodificación). Después, tiene que entender lo que significan las palabras (vocabulario). Tiene que entender cómo encajan las palabras en una frase (sintaxis). Por último, la comprensión proviene de la unión de estas piezas para crear un significado.

La mayoría de los alumnos de 6º curso podrían leer el problema de la Sra. Hartwell y entender fácilmente que Sarah está repartiendo zanahorias a sus caballos. Pero muchos menos relacionarán el «reparto» de zanahorias con la división.

Esta es la parte que hace tropezar a muchos educadores. Nos parece tan obvio. «Está repartiendo literalmente las zanahorias. Cómo no van a ver que es una división».

Simplemente no lo ven. Si lo hicieran, no verías gráficos de palabras clave colgados en las aulas de matemáticas. Y todo se remonta a cuando enseñamos las operaciones por primera vez.

Por qué los alumnos luchan con la formulación

Muchos profesores de muchos colegios enseñan a los alumnos que las matemáticas son una asignatura con sentido. Pero en otros, las matemáticas se enseñan como una asignatura para recordar.

Un ejemplo de «matemáticas como recuerdo» es cuando los estudiantes memorizan datos matemáticos. Pero los algoritmos también son para recordar. Poner 120 encima de 47. Sigue estos pasos para sumar, estos para restar y estos para multiplicar.

Los alumnos pueden repetir estos pasos sin entender el tamaño de los números o incluso lo que significan las operaciones.

Cuando empezamos con conceptos (utilizando modelos visuales o frases numéricas), los alumnos aprenden lo que significan las operaciones. Cuando pasamos directamente a un algoritmo, los alumnos piensan en las operaciones como una serie de pasos aleatorios.

Año tras año, hacemos que los alumnos recuerden y repitan. Completan el mismo algoritmo 30 veces para los deberes. Cambia los números, y el proceso sigue siendo el mismo. Pero dales un problema de palabras, y ahora tienen que tener sentido.

Lo que las pruebas nos dicen sobre el razonamiento

Podríamos dar a nuestros alumnos 10 problemas con el título «Problemas de palabras de división», para que sea más fácil. Ni siquiera tendrán que leer los problemas. Sólo tienen que averiguar (o adivinar) qué número es el divisor y cuál es el dividendo.

Pero cuando los estudiantes se presentan a un examen estatal, el objetivo no es hacerlo más fácil. El objetivo es evaluar lo que pueden hacer por sí mismos.

Los que hacen los exámenes no quieren decirles qué operación deben utilizar. Incluso pondrán palabras clave para la división y la suma en el mismo problema. «Hay 20 alumnos en la clase. Si cada niño tiene tres dólares, ¿cuánto tienen en total?».

Así que cuando los estudiantes tienen problemas con los problemas de palabras, no se trata sólo de los problemas de palabras. Suele significar que están haciendo matemáticas de memoria. Tenemos que enseñarles que las matemáticas tienen que ver con la creación de sentido.

Los estudiantes necesitan estrategias y procesos para resolver problemas de palabras

Parte del problema con un sistema como CUBES es que se llama a sí mismo estrategia, pero en realidad es un proceso.

Un proceso es una serie de pasos. Una vez que identificas un proceso eficiente, puedes repetirlo una y otra vez sin pensar demasiado. Los algoritmos son un proceso. Como lo es alinear «del más alto al más bajo» para ir a comer.

Una estrategia es diferente. Las estrategias requieren una comprensión profunda. Y la capacidad de aplicar la comprensión en nuevas situaciones.

No podemos preparar a los estudiantes para cada escenario que encontrarán en un problema de palabras. Algunos requieren que combinen diferentes habilidades matemáticas que nunca han combinado antes. O pueden requerir que los estudiantes cambien el orden de los pasos para llegar a la solución correcta.

Considere lo siguiente:

Tiene 5 galones de jugo para un evento escolar con 100 estudiantes. Si en cada vaso caben 3 onzas, ¿cuántos vasos puede beber cada alumno? Cuánto sobrará.

Un proceso de resolución de problemas puede ayudar a los estudiantes a comenzar a abordar este problema. «Identificar lo que se pide». «Considerar qué información se está dando»

Pero no hay un proceso establecido que podamos enseñarles para resolverlo realmente. Ahí es donde entra la estrategia. Tienen que convertir las unidades. Reconocer que estamos dividiendo con restos, en lugar de dividir completamente. También es probable que deban reordenar las operaciones, dividiendo el zumo en vasos antes de dividirlo por el número de alumnos.

No hay ningún «truco» que lleve a los alumnos hasta ahí. Necesitan entender el significado de las operaciones. Necesitan entender las matemáticas como un tema de creación de sentido. Y necesitan practicar repetidamente la aplicación del pensamiento estratégico a los problemas de palabras.

El proceso de Pólya para resolver problemas de palabras

George Pólya fue un influyente matemático húngaro y profesor de Stanford que encontró un proceso que podía utilizarse para resolver cualquier problema. Su trabajo ha tocado a innumerables matemáticos y educadores, la mayoría de los cuales no conocen su nombre.

De hecho, los CUBOS y otras de las llamadas estrategias de resolución de problemas se basan vagamente en su trabajo. El problema es que tratan de simplificarlo. En el proceso, eliminan cualquier cosa que se parezca al pensamiento profundo.

Polya creía que todo problema podía resolverse en cuatro pasos: Comprender, Planificar, Resolver y Reflexionar. Creo que el proceso original de cuatro pasos de Polya está bien para usarlo en las escuelas.

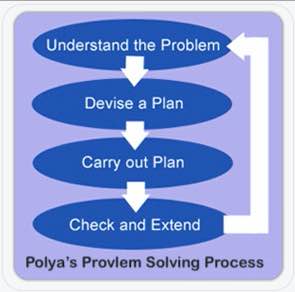Para entender el problema, identificamos qué información se da y qué queremos encontrar. De ahí viene la ‘C’ y la ‘U’ de los cubos. Si los alumnos quieren rodear los números y subrayar la pregunta, bien. Yo prefiero que los escriban (con las unidades) en un organizador gráfico, al menos al principio. Esto les ayuda a procesar lo que están leyendo. También me ayuda a mí, como profesor, a evaluar su comprensión mientras recorro el aula.

A continuación viene la parte complicada. El «plan» es donde formulamos el problema. Estamos tomando un escenario del mundo real y convirtiéndolo en otra representación matemática.

El tercer paso es resolver. Si hemos formulado correctamente, aquí es donde calculamos. Los alumnos suelen utilizar un algoritmo, pero yo animo a utilizar también ecuaciones y modelos visuales.

Por último, los alumnos miran hacia atrás y comprueban su trabajo. También deben reflexionar sobre su proceso. Si he cometido un error, ¿por qué? ¿Podría esta estrategia ayudarme a resolver problemas similares en el futuro?

Estrategias para resolver problemas de palabras

Tener un proceso para abordar los problemas de palabras es definitivamente útil. Pero no podemos pretender que las matemáticas significativas se aprendan sólo siguiendo pasos. El objetivo de los problemas de palabras es ampliar las matemáticas más allá de los «hechos matemáticos» y los algoritmos.

Hay algunas estrategias útiles para ayudar a los estudiantes con la formulación. Al principio, enseño explícitamente una serie de estrategias diferentes.

A medida que enseño las estrategias, hago que los estudiantes resuelvan problemas que van bien con esa estrategia. Algunos tipos de problemas van muy bien con ‘Adivina y comprueba’. Otros son más adecuados para ‘Haz un dibujo’.

Al final, les doy problemas de palabras desafiantes que se pueden resolver de varias maneras. Una vez que tienen las herramientas en su cinturón de herramientas, pueden elegir cuál es la mejor para la situación.

La combinación de estrategias también puede ser muy eficaz. Por ejemplo, hacer un dibujo a menudo puede ser útil para ayudar a la formulación. Si un agricultor tiene 18 hileras de zanahorias y 10 zanahorias en cada hilera, un alumno puede empezar dibujando el campo. En algún momento, pueden pensar «Vaya, esto es una matriz», y se dan cuenta de que pueden multiplicar utilizando la matemática mental, una expresión o un algoritmo.

Otras veces, los estudiantes pueden utilizar modelos visuales para formular y resolver el problema.

Ayuda a tus alumnos a afrontar problemas de palabras desafiantes

Si eres como muchos profesores, puede que te preocupe cómo manejarán todo esto tus alumnos. Procesos, estrategias, pensamiento crítico… hay mucho en juego.

Incluso puede estar pensando que los problemas de palabras parecían más fáciles antes de este artículo. Si es así, te pido disculpas.

La clave es no agobiarse intentando hacerlo todo a la vez. Empieza por resolver un problema de palabras sencillo utilizando el proceso de Polya. Luego, introduce una nueva estrategia cada semana. Al final del año, se sorprenderá de lo lejos que han llegado.

Tal vez esté interesado en profundizar en la resolución creativa de problemas. Considere la posibilidad de asistir a un taller práctico de matemáticas o de trabajar con un entrenador en línea.

Si está listo para llevar algo de Polya a su aula mañana, este organizador gráfico es una gran manera de empezar. Le servirá de andamiaje para el proceso de cuatro pasos y le ayudará a identificar dónde se desvían sus alumnos.

Organizador gratuito de problemas de palabras

Acerca del autor

Jeff Lisciandrello es el fundador de Room to Discover y un consultor educativo especializado en el aprendizaje centrado en el estudiante. Su diseño de 3 puentes para el aprendizaje ayuda a las escuelas a explorar prácticas innovadoras dentro de los entornos tradicionales. Le gusta ayudar a los educadores a adoptar enfoques de instrucción basados en la investigación y personalizados. Puedes conectar con él a través de Twitter @EdTechJeff