Existují různé typy grafů v závislosti na počtu vrcholů, počtu hran, propojenosti a jejich celkové struktuře. V této kapitole se budeme zabývat jen některými důležitými typy grafů.
Nulový graf
Graf, který nemá žádné hrany, se nazývá nulový graf.
Příklad

V uvedeném grafu jsou tři vrcholy pojmenované ‚a‘, ‚b‘ a ‚c‘, ale nejsou mezi nimi žádné hrany. Jedná se tedy o nulový graf.
Triviální graf
Graf s jediným vrcholem se nazývá triviální graf.
Příklad
Ve výše zobrazeném grafu je pouze jeden vrchol ‚a‘ bez dalších hran. Jedná se tedy o triviální graf.
Neorientovaný graf
Neorientovaný graf obsahuje hrany, ale tyto hrany nejsou orientované.
Příklad
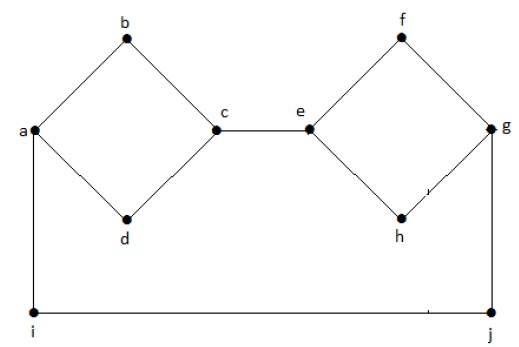
V tomto grafu jsou vrcholy „a“, „b“, „c“, „d“, „e“, „f“, „g“ a hrany grafu „ab“, „bc“, „cd“, „da“, „ag“, „gf“, „ef“. Protože se jedná o neorientovaný graf, jsou hrany „ab“ a „ba“ stejné. Podobně jsou uvažovány i ostatní hrany.
Směrovaný graf
V směrovaném grafu má každá hrana směr.
Příklad
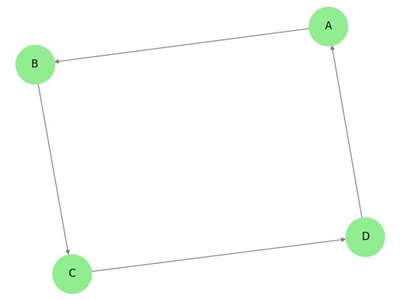
V uvedeném grafu máme sedm vrcholů ‚a‘, ‚b‘, ‚c‘, ‚d‘, ‚e‘, ‚f‘ a ‚g‘ a osm hran ‚ab‘, ‚cb‘, ‚dc‘, ‚ad‘, ‚ec‘, ‚fe‘, ‚gf‘ a ‚ga‘. Protože se jedná o směrový graf, je každá hrana označena šipkou, která ukazuje její směr. Všimněte si, že v orientovaném grafu se ‚ab‘ liší od ‚ba‘.
Jednoduchý graf
Graf bez smyček a bez paralelních hran se nazývá jednoduchý graf.
-
Maximální možný počet hran v jednom grafu s ‚n‘ vrcholy je nC2, kde nC2 = n(n – 1)/2. V grafu s ‚n‘ vrcholy je nC2.
-
Počet možných jednoduchých grafů s ‚n‘ vrcholy = 2nc2 = 2n(n-1)/2.
Příklad
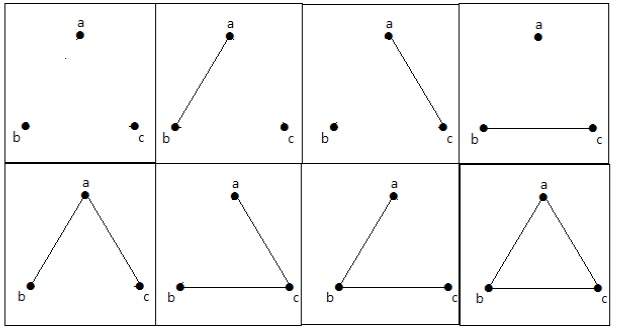
V následujícím grafu jsou 3 vrcholy se 3 hranami, což je maximum bez paralelních hran a smyček. To lze dokázat pomocí výše uvedených vzorců.
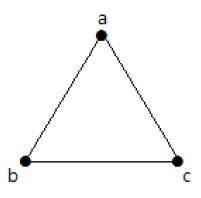
Maximální počet hran s n=3 vrcholy –
nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
Maximální počet jednoduchých grafů s n=3 vrcholy –
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
Těchto 8 grafů je uvedeno níže –
Spojitý graf
O grafu G se říká, že je spojitý, jestliže mezi každou dvojicí vrcholů existuje cesta. Pro každý vrchol grafu by měla existovat alespoň jedna hrana. Abychom mohli říci, že je spojen s nějakým jiným vrcholem na druhé straně hrany.
Příklad
V následujícím grafu má každý vrchol svou hranu spojenou s jinou hranou. Jedná se tedy o spojitý graf.
Nespojitý graf
Graf G je nespojitý, jestliže neobsahuje alespoň dva spojené vrcholy.
Příklad 1
Následující graf je příkladem nespojitého grafu, kde jsou dvě komponenty, jedna s vrcholy „a“, „b“, „c“, „d“ a druhá s vrcholy „e“, „f“, „g“, „h“.
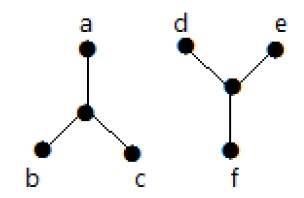
Dvě komponenty jsou nezávislé a nejsou navzájem spojeny. Proto se nazývá nespojitý graf.
Příklad 2
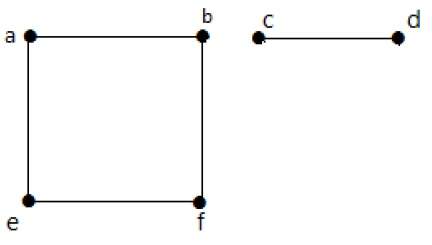
V tomto příkladu jsou dvě nezávislé komponenty, a-b-f-e a c-d, které nejsou navzájem spojeny. Jedná se tedy o nespojitý graf.
Regulární graf
O grafu G se říká, že je regulární, jestliže všechny jeho vrcholy mají stejný stupeň. Je-li v grafu stupeň každého vrcholu „k“, pak se graf nazývá „k-regulární graf“.
Příklad
V následujících grafech mají všechny vrcholy stejný stupeň. Tyto grafy se tedy nazývají regulární grafy.
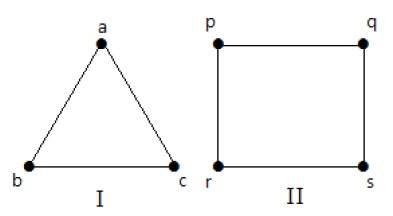
V obou grafech mají všechny vrcholy stupeň 2.

V obou grafech mají všechny vrcholy stupeň 2. Říká se jim 2-regulární grafy.
Úplný graf
Jednoduchý graf s ‚n‘ vzájemnými vrcholy se nazývá úplný graf a označuje se ‚Kn‘. V grafu by měl mít vrchol hrany se všemi ostatními vrcholy, pak se nazývá úplný graf.
Jinými slovy, je-li vrchol spojen se všemi ostatními vrcholy v grafu, pak se nazývá úplný graf.
Příklad
V následujících grafech je každý vrchol v grafu spojen se všemi zbývajícími vrcholy v grafu kromě sebe sama.
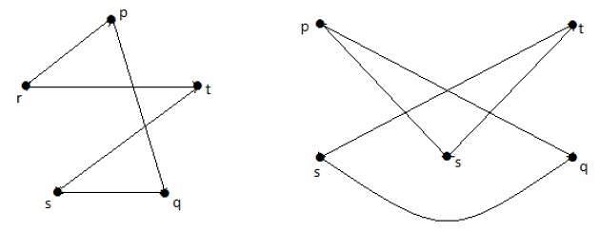
V grafu I,
| a | b | c | |
|---|---|---|---|
| a | Není spojeno | Spojeno | Spojeno |
| b | Připojeno | Nepřipojeno | Připojeno |
| c | Připojeno | Připojeno | Nepřipojeno |
V grafu II,
| p | q | r | s | ||
|---|---|---|---|---|---|
| p | Nezapojený | Zapojený | Zapojený | Zapojený | Připojeno |
| q | Připojeno | Nepřipojeno | Připojeno | Připojeno | |
| r | Připojeno | Připojeno | Nepřipojeno | Připojeno | |
| s | Připojeno | Připojeno | Nepřipojeno | Připojeno | Nepřipojeno Spojitý |
Cyklický graf
Jednoduchý graf s ‚n‘ vrcholy (n >= 3) a ‚n‘ hranami se nazývá cyklický graf, jestliže všechny jeho hrany tvoří cyklus délky ‚n‘.
Jestliže je stupeň každého vrcholu v grafu roven dvěma, pak se nazývá cyklický graf.
Notace – Cn
Příklad
Podívejte se na následující grafy –
-
Graf I má 3 vrcholy se 3 hranami, které tvoří cyklus ‚ab-bc-ca‘.
-
Graf II má 4 vrcholy se 4 hranami, které tvoří cyklus ‚pq-qs-sr-rp‘.
-
Graf III má 5 vrcholů s 5 hranami, které tvoří cyklus ‚ik-km-ml-lj-ji‘.
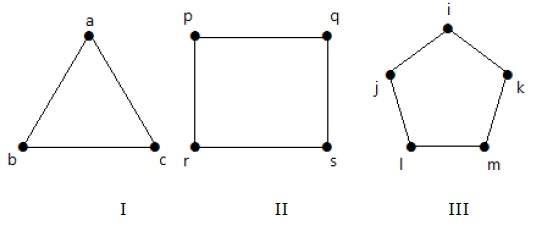
Všechny uvedené grafy jsou tedy cyklické grafy.
Kolový graf
Kolový graf získáme z cyklického grafu Cn-1 přidáním nového vrcholu. Tento nový vrchol se nazývá náboj, který je spojen se všemi vrcholy Cn.
Notace – Wn
No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)
Příklad
Podívejte se na následující grafy. Všechny jsou kolové grafy.
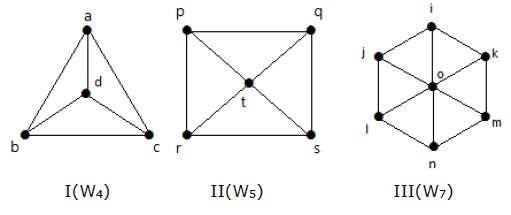
V grafu I jej získáme z grafu C3 přidáním vrcholu uprostřed pojmenovaného jako ‚d‘. Označujeme jej jako W4.
Number of edges in W4 = 2(n-1) = 2(3) = 6
V grafu II jej získáme z grafu C4 přidáním vrcholu uprostřed pojmenovaného jako ‚t‘. Je označen jako W5.
Number of edges in W5 = 2(n-1) = 2(4) = 8
V grafu III se získá z C6 přidáním vrcholu uprostřed s názvem „o“. Označujeme ho jako W7.
Number of edges in W4 = 2(n-1) = 2(6) = 12
Cyklický graf
Graf s alespoň jedním cyklem se nazývá cyklický graf.
Příklad
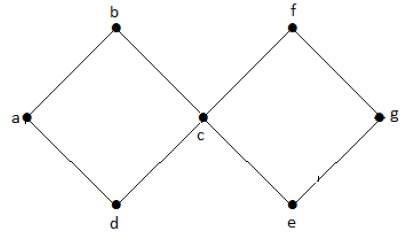
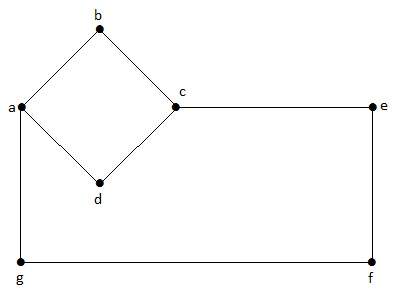
V uvedeném příkladovém grafu máme dva cykly a-b-c-d-a a c-f-g-e-c. V tomto grafu jsou dva cykly. Proto se nazývá cyklický graf.
Acyklický graf
Graf bez cyklů se nazývá acyklický graf.
Příklad
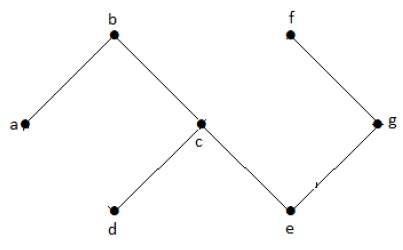
V uvedeném příkladovém grafu nemáme žádné cykly. Jedná se tedy o necyklický graf.
Bipartitní graf
Jednoduchý graf G = (V, E) s rozdělením vrcholů V = {V1, V2} se nazývá bipartitní graf, jestliže každá hrana E spojuje vrchol ve V1 s vrcholem ve V2.
Obecně má bipertitní graf dvě množiny vrcholů, řekněme V1 a V2, a pokud je nakreslena hrana, měla by spojovat libovolný vrchol z množiny V1 s libovolným vrcholem z množiny V2.
Příklad
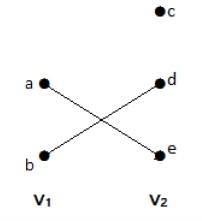
V tomto grafu můžete pozorovat dvě množiny vrcholů – V1 a V2. Zde dvě hrany pojmenované ‚ae‘ a ‚bd‘ spojují vrcholy dvou množin V1 a V2.
Úplný bipartitní graf
O bipartitním grafu ‚G‘, G = (V, E) s rozdělením V = {V1, V2} se říká, že je úplný bipartitní graf, jestliže každý vrchol ve V1 je spojen s každým vrcholem V2.
Obecně platí, že úplný bipartitní graf spojuje každý vrchol z množiny V1 s každým vrcholem z množiny V2.
Příklad
Následující graf je úplný bipartitní graf, protože má hrany spojující každý vrchol z množiny V1 s každým vrcholem z množiny V2.
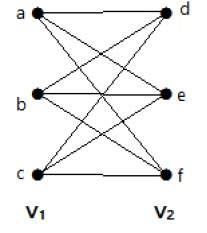
Pokud |V1| = m a |V2| = n, pak úplný bipartitní graf označíme Km, n.
-
Km,n má (m+n) vrcholů a (mn) hran.
-
Km,n je regulární graf, jestliže m=n.
Obecně není úplný bipartitní graf úplný graf.
Km,n je úplný graf, jestliže m=n=1.
Maximální počet hran v bipartitním grafu s n vrcholy je
Jestliže n=10.
Jestliže n=10, je maximální počet hran v bipartitním grafu s n vrcholy, k5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25
Podobně K6, 4=24
K7, 3=21
K8, 2=16
K9, 1=9
Pokud n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20
Podobně K6, 3=18
K7, 2=14
K8, 1=8
„G“ je bipartitní graf, jestliže „G“ nemá cykly liché délky. Speciálním případem bipartitního grafu je hvězdicový graf.
Hvězdicový graf
Úplný bipartitní graf tvaru K1, n-1 je hvězdicový graf s n-vrcholy. Hvězdicový graf je úplný bipartitní graf, jestliže jediný vrchol patří do jedné množiny a všechny zbývající vrcholy patří do druhé množiny.
Příklad
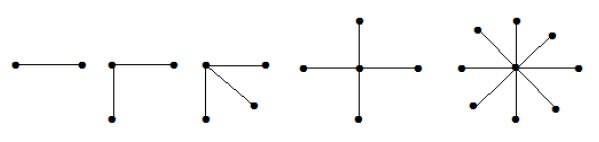
V uvedených grafech jsou z ‚n‘ vrcholů všechny vrcholy ‚n-1‘ spojeny s jediným vrcholem. Proto má tvar K1, n-1, což jsou hvězdicové grafy.
Komplement grafu
Nechť ‚G-‚ je jednoduchý graf s některými vrcholy jako ‚G‘ a hrana {U, V} je přítomna v ‚G-‚, pokud tato hrana není přítomna v G. To znamená, že dva vrcholy jsou sousední v ‚G-‚, pokud tyto dva vrcholy nejsou sousední v G. To znamená, že dva vrcholy jsou sousední v ‚G-‚.
Pokud hrany, které existují v grafu I, chybí v jiném grafu II, a pokud jsou graf I i graf II spojeny dohromady a tvoří úplný graf, pak se graf I a graf II nazývají vzájemné doplňky.
Příklad
V následujícím příkladu má graf-I dvě hrany ‚cd‘ a ‚bd‘. Jeho komplement graf-II má čtyři hrany.
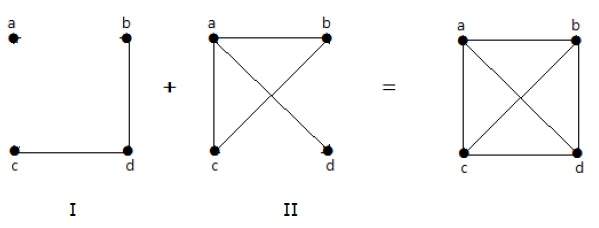
Všimněte si, že hrany v grafu-I nejsou přítomny v grafu-II a naopak. Proto kombinace obou grafů dává úplný graf o ‚n‘ vrcholech.
Poznámka – kombinace dvou komplementárních grafů dává úplný graf.
Je-li ‚G‘ libovolný jednoduchý graf, pak
|E(G)| + |E(‚G-‚)| = |E(Kn)|, kde n = počet vrcholů v grafu.
Příklad
Nechť ‚G‘ je jednoduchý graf s devíti vrcholy a dvanácti hranami, najděte počet hran v ‚G-‚.
Máte, |E(G)| + |E(‚G-‚)| = |E(Kn)|
12 + |E(‚G-‚)| =
.