Úvod
Tato stránka obsahuje přehled rovnice kontinuity, která vynucuje zachování hmotnosti v Eulerově analýze. Nejedná se o striktní popis chování materiálu, ale výsledná rovnice se často používá jako identita proalgebraickou manipulaci s konstitutivními modely popisujícími chování materiálu. Stojí tedy za to si ji zopakovat. Je také klíčová pro analýzu proudění tekutin, protože klasické analýzy tekutin nemohou být Lagrangeovy, protože polohy všech částic tekutiny v okamžiku \(t = 0\) nejsou známy.
Zachování hmotnosti
Rovnice kontinuity odráží skutečnost, že hmotnost se zachováváv každé analýze nejaderné mechaniky kontinua. Rovnice je vytvořena sečtením rychlostí, kterými hmota proudí do a z řídicího objemu, a stanovením čistého přítoku rovného rychlosti změny hmotnosti v něm. To je demonstrováno na následujícím obrázku.
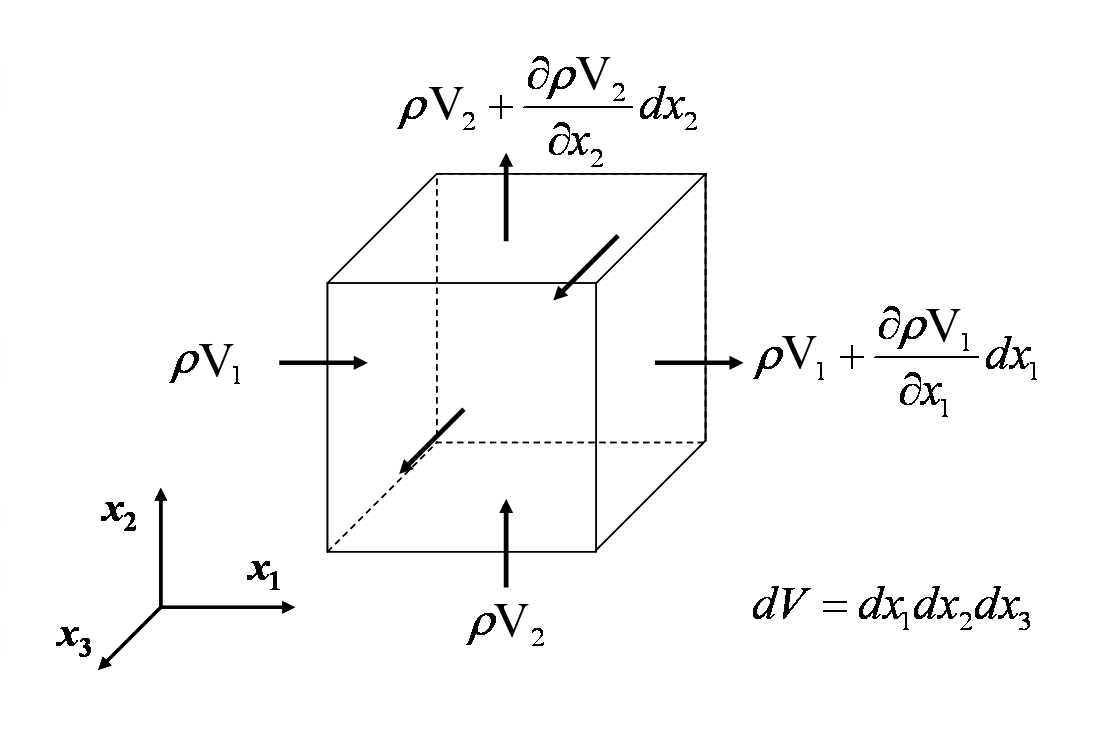
Vyrovnáním všech rychlostí hmotnostního toku do a z diferenciálního regulačního objemu získáme
\
Zrušením členů a dělením \(dx_1 dx_2 dx_3\). dostaneme
\
a přeuspořádáním dostaneme
\
To lze stručně zapsat jako
\

Důležité body
Tyto jsou konečné, úplné a nejobecnější tvary spojité rovnice, která vynucuje zachování hmotnosti. Platí pro všechny materiály,nejen pro kapaliny. Platí tedy i pro pevné látky. Všimněte si, že se jedná o jedinou skalární rovnici, která má eulerovský charakter, protože gradientní členy jsou \({\část \nad \část x_i}\), nikoli \({\část \nad \část X_i}\).
Někoho by mohlo zajímat, zda k eulerovské formě této rovnice existuje nějaký lagrandovský protějšek. Existuje. Obvykle se zapisuje jako
\
To jednoduše říká, že diferenciální kus hmoty v deformovaném stavu\(\rho \, dV\) se musí rovnat své původní hodnotě\(\rho_o dV_o\) v nedeformovaném stavu.
Existuje několik speciálních případů rovnice kontinuity.První nastává, když je tok ustálený. V tomto případě je derivace vzhledem k času nulová, takže.
\
Druhým zvláštním případem je případ nestlačitelnosti, tj, \(\rho = \)konstantní.V tomto případě je derivace vzhledem k času nulová a \(\rho\) lze z rovnice odečíst, takže zbývá pouze
\
Tento výsledek je natolik jednoduchý, že se často rozšiřuje.
\
Všimněte si, že to není nic jiného než \(\text{tr}({\bf D}) = 0\) pro případ nestlačitelných materiálů.

Derivát materiálu
Následující stojí za pozornost, protože umožňuje oddělit vektor hustoty a vektor rychlosti. Prvním krokem je použití součinového pravidla na divergentní člen v rovnici spojitosti.
\
A pak si všimněte, že\({\část \rho \nad \část t} + {\bf v} \cdot \nabla \rho\)je právě hmotnou derivací hustoty,\({D \rho \nad D t}\).
Takže rovnici kontinuity lze také zapsat jako
\
Je-li materiál nestlačitelný, pak se \(\rho\) nemůže měnit, takže\( {D \rho \over D t} \) musí být nulová, zbývá
\
A pak vydělíme \(\rho\) (protože není nulové) a dostaneme
\

Rovnice kontinuity Příklad
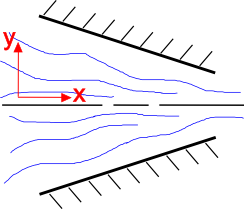
Je intuitivní, že proudění tekutiny se zrychluje se zmenšováním průřezu, jak je znázorněno vpravo. To vysvětluje rovnice kontinuity. Uvažujme 2-D pole ustáleného proudění nestlačitelné tekutiny.Rovnice kontinuity pro tuto situaci je
\
Začněte tím, že se podíváte na y-ovou složku proudění, \(v_2\). Geometrie sbíhající se trysky nutí složku \(v_2\) proudit nahoru, když \(y \lt 0\), a proudit dolů, když \(y \gt 0\). Takže \(v_2 \gt 0\), když \(y \lt 0\) a \(v_2 \lt 0\), když \(y \gt 0\).
Čistý efekt toho je, že \({\část v_2 \nad \část x_2} \lt 0\)v konvergující trysce.
Ale rovnice kontinuity říká, že součet obou parciálních derivací se musí rovnat nule. Pokud je tedy druhá derivace menší než nula, pak
\
A to znamená, že proudění kapaliny musí být zrychlující.
.