Stejně jako u dortu můžete mít 2 malé kousky nebo 1 dvakrát větší a je to stejné množství. Proto je mnoho zlomků ekvivalentních, například 2/5 a 4/10.


Každé číslo lze zapsat jako zlomek
Zapište libovolné celé číslo větší než 1 tak, aby bylo zlomkem, protože celkový počet částí v libovolném nedělitelném celku je jedna.
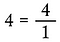
Násobení zlomků napříč
Násobení zlomků je snadné, stačí násobit napříč.
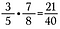
Poznámka: Smíšená čísla je třeba nejprve převést na nesprávné zlomky, přečtěte si o tom více.
Násobení libovolným tvarem jedničky kdykoli
Číslo 1 se nazývá multiplikativní identita, protože ho můžeme násobit libovolným číslem a číslo zůstane stejné. To je důležité pro zlomky, protože často potřebujeme změnit vzhled zlomku, aniž bychom ve skutečnosti změnili jeho hodnotu.
Například násobením 3/3 mohu změnit 1/3 na ekvivalentní zlomek 3/9. To znamená, že násobením 3/3 změníme hodnotu zlomku.
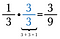
Sčítání a odčítání stejně velkých částí
Při sčítání a odčítání zlomků musí být jmenovatelé stejní. To dává smysl. Pokud chceme části spojovat nebo odebírat, musíme mluvit o stejně velkých částech, jinak by to bylo nepřehledné.
Co tedy dělat, když zlomky nemají stejnou velikost?“
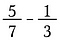
Násobení tvarem jedna změní jmenovatele na společnou velikost. V podstatě rozdělujeme zlomky na menší velikostní části, dokud nemají stejnou velikost. Tomu se říká hledání společného jmenovatele.
Pravdu řečeno, stačí jakýkoli společný jmenovatel, ale lidé dávají přednost hledání toho nejmenšího. V tomto případě je nejmenším číslem, do kterého se vejde 7 i 3 beze zbytku, číslo 21. První zlomek tedy vynásobte číslem 3/3 a druhý číslem 7/7.
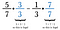
Pokud vás nenapadá nejmenší společný jmenovatel, můžete vždy každý zlomek vynásobit opačným jmenovatelem. Někdy, jako v tomto případě, se ukáže, že to je nejmenší společný jmenovatel. Pokud tomu tak není, stačí odpověď na konci zmenšit.
Pokud se jmenovatelé shodují, odečtěte čitatele a získáte 8/21.
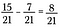
Toto funguje tak, jak se dalo očekávat. Obrázkově začneme s 15 dílky z celkových 21.

Odstraňte obarvení ze 7 z 15 modrých bloků.

Podle očekávání zbývá 8/21.
Nejprve vyměňte smíšená čísla
Smíšené číslo je kombinace celého čísla a zlomku.
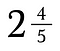
Smíšená čísla nehrají dobře s jinými zlomky. Je dobré je nejprve převést na nepravé zlomky.
Poznámka: Nepravý zlomek je zlomek, jehož čitatel je větší než jmenovatel, má tedy hodnotu větší než jedna.
Převod smíšeného čísla je vlastně sčítání
Převod 2 a 4/5 na nepravý zlomek provedeme tak, že sečteme 2 + 4/5.
Krok 1: Začneme tím, že číslo 2 přepíšeme jako 2/1. Při převodu na nepravý zlomek sečteme 2 a 4/5. Při převodu na nepravý zlomek sečteme 2 a 4/5.
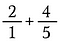
Krok 2: Vynásobte 2/1 5/5, čímž získáte ekvivalentní zlomek 10/5, který má požadovaného společného jmenovatele 5.
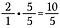
Krok 3: Sečteme 10/5 + 4/5.
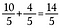
Náš výsledek je ekvivalentní nesprávný zlomek 14/5.
Pro převod zpět na smíšené číslo proveď dělení. Například 5 přejde dvakrát ve 14 (protože 5 x 2 = 10) a zbydou 4 dílky.
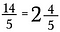
Porovnání zlomků pomocí křížového součinu
Předpokládejme, že chceme určit, který je větší: 5/12 nebo 6/13.
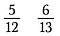
První krok: Vynásobte úhlopříčku a součin napište nad čitatele.
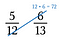
Krok druhý: Vynásobte druhou úhlopříčku a její součin zapište nad jejího čitatele.
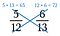
Krok třetí: Porovnejte výrobky. Strana s větším součinem je větší zlomek. V tomto případě je tedy 5/12 menší než 6/13.
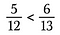
Jestliže jsou zlomky stejné, můžeme určit i pomocí křížových součinů.
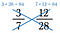
Křížový součin 3/7 a 12/28 je 84, proto 3/7 = 12/28.
Zrušíme cokoli, co se dělí jedničkou
Nejlepší na zlomcích je, že se dá najít spousta možností, jak je zrušit. Díky tomu je lze snadno a rychle zvládnout.
Předpokládejme, že mám zlomek 8/10. Jaký zlomek? Jak 8, tak 10 lze přepsat s 2 jako činitelem.
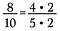
Protože 2/2 = 1, mohu dvojku zrušit a jako zmenšený zlomek zůstane 4/5.
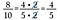
Tuto strategii využiji i k usnadnění násobení zlomků.
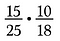
Začněte přepisem jednotlivých čísel na činitele.
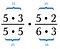
Zrušte všechny dvojice čísel, které se dělí 1. Například 5/5 = 1.
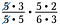
Mám další dvojici pětek i dvojici trojek, které se také dělí na 1. Pokud je to možné, vymažte dvojici pětek.
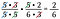
Oops! Mohl jsem přepsat 6 jako 2 x 3 a zrušit dvojici dvojek. Nevadí, když nějaký činitel vynecháš, prostě pokračuj, dokud je všechny nezískáš.
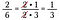
Pokud bych násobil 15/25 krát 10/18 přímo, bylo by to hodně aritmetické, pomocí rušení zlomky předem zmenším a zjednoduším násobení.
Použití násobení k dělení zlomků
Představa dělení zlomků je snadná na jednoduchých příkladech, například:

V celku jsou dvě poloviny, proto je v 5 celcích 10 polovin.
Představa se však stává složitější u složitějších zlomků.
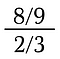
K řešení tohoto problému využijeme dvě skutečnosti:
- Můžeme násobit libovolným tvarem jedničky (tj.tj. cokoli nad sebou samým)
- Násobení reciprokou hodnotou 3/2, což je 2/3, vede k 1 prostřednictvím zrušení
Kroku jedna:
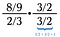
Nyní máme k řešení dvě menší úlohy (modrou a zelenou).
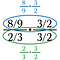
Krok druhý: Zrušte vše, co se ve spodním (zeleném) zlomku dělí 1. Výsledkem by měla být vždy 1.

Nyní nám zbývá vyřešit horní úlohu.
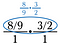
Třetí krok: Pomocí rušení předem zredukujte zlomek. Po provedení těchto redukcí vynásobte napříč a získáte 4/3.

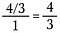
Zkratka
Jedná se o mechaniku dlouhé ruky „převrať a vynásob.“
Můžeme vynechat násobení reciprokou hodnotou dole, protože ta se vždy ruší na 1. Stačí tedy vynásobit čitatele reciprokou hodnotou jmenovatele.

Bonus: Teorie, kdyby vás to zajímalo…
Skvělá otázka! Pro zobecnění vytvořte dva zlomky pomocí písmen a, b, c a d, které představují čtyři různá čísla.
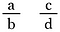
Oběma zlomky vynásobte b-d (to nám umožní zrušit jmenovatele).
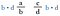
Nyní zrušíme b na levé straně a d na pravé straně, protože se dělí na 1. Už nemáme zlomky, jen součin d-a a c-b.
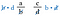
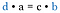
Podívejte se zpět na původní zlomky. Jedná se o stejné součin, jako kdybychom násobili úhlopříčky. Proto zkratka spočívá v porovnání křížového součinu.
❤ STAY CONNECTED ❤
Sledujte vše, co Math Hacks chystá!