Nedávno mi jeden kolega položil několik otázek typu: „Proč máme tolik aktivačních funkcí?“, „proč zrovna tahle funguje lépe než jiná?“, „jak poznáme, kterou použít?“, „je to hardcore matematika?“ a tak dále. Tak jsem si řekl, proč o tom nenapsat článek pro ty, kteří se s neuronovou sítí seznamují jen na základní úrovni, a proto je zajímají aktivační funkce a jejich „proč-jak-matematika!“.
POZNÁMKA: Tento článek předpokládá, že máte základní znalosti o umělém „neuronu“. Pro lepší pochopení bych doporučil přečíst si před čtením tohoto článku základy neuronových sítí.
Aktivační funkce
Co tedy umělý neuron dělá? Jednoduše řečeno, vypočítá „vážený součet“ svých vstupů, přidá zkreslení a pak rozhodne, zda má být „vystřelen“, nebo ne ( ano, správně, to dělá aktivační funkce, ale pojďme na chvíli s proudem ).
Uvažujme tedy neuron.
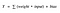
Nyní může být hodnota Y jakákoli v rozsahu od -inf do +inf. Neuron ve skutečnosti nezná hranice této hodnoty. Jak tedy rozhodneme, zda má neuron vypálit, nebo ne ( proč právě tento vzorec vypalování? Protože jsme se to naučili z biologie, takhle funguje mozek a mozek je pracovní výpovědí úžasného a inteligentního systému ).
Pro tento účel jsme se rozhodli přidat „aktivační funkce“. Aby bylo možné zkontrolovat hodnotu Y produkovanou neuronem a rozhodnout, zda mají vnější spojení považovat tento neuron za „vystřelený“, nebo ne. Nebo spíše řekněme – „aktivován“, nebo ne.
Aktivační funkce
První věc, která nás napadla, je, co takhle aktivační funkce založená na prahu? Pokud je hodnota Y vyšší než určitá hodnota, prohlásíme ji za aktivovanou. Pokud je menší než prahová hodnota, prohlásíme, že není aktivován. Hmm skvělé. To by mohlo fungovat!
Aktivační funkce A = „aktivována“, pokud Y > práh, jinak ne
Alternativně A = 1, pokud y> práh, 0 jinak
No, to, co jsme právě udělali, je „kroková funkce“, viz následující obrázek.
Jeho výstup je 1 ( aktivuje se), když hodnota > 0 (práh), a výstupem je 0 ( neaktivuje se), jinak.
Skvělé. Takto tedy vzniká aktivační funkce pro neuron. Žádné zmatky. Má to však určité nevýhody. Pro lepší pochopení se zamyslete nad následujícím.
Předpokládejme, že vytváříte binární klasifikátor. Něco, co má říci „ano“ nebo „ne“ ( aktivovat nebo neaktivovat ). To by za vás mohla udělat funkce Step! Přesně to dělá, řekne 1 nebo 0. Nyní se zamyslete nad případem použití, kdy byste chtěli zapojit více takových neuronů, abyste přinesli více tříd. Třída1, třída2, třída3 atd. Co se stane, když se „aktivuje“ více než 1 neuron. Všechny neurony budou mít na výstupu hodnotu 1 ( z krokové funkce). Jak byste se nyní rozhodli? Která třída to je? Hmm těžké, složité.
Chtěli byste, aby síť aktivovala pouze 1 neuron a ostatní měly hodnotu 0 ( teprve pak byste mohli říci, že správně klasifikovala/identifikovala třídu ). Aha, takhle se to hůř trénuje a konverguje. Bylo by lepší, kdyby aktivace nebyla binární a místo toho by říkala „aktivováno 50 %“ nebo „aktivováno 20 %“ atd. A pak, pokud se aktivuje více než 1 neuron, by se dalo zjistit, který neuron má „nejvyšší aktivaci“ a tak dále ( lépe než max, softmax, ale to zatím nechme být ).
I v tomto případě, pokud více než 1 neuron řekne „100% aktivován“, problém stále přetrvává. já vím! Ale..protože existují mezilehlé aktivační hodnoty pro výstup, může být učení plynulejší a jednodušší ( méně váhavé ) a šance, že více než 1 neuron bude 100% aktivován, je menší ve srovnání s krokovou funkcí při trénování ( také v závislosti na tom, co trénujete a na datech ).
Ok, takže chceme něco, co nám dá mezilehlé ( analogové ) aktivační hodnoty, spíše než říkat „aktivován“ nebo ne ( binární ).
První, co nás napadne, bude lineární funkce.
Lineární funkce
A = cx
Přímková funkce, kde aktivace je úměrná vstupu ( což je vážený součet z neuronu ).
Takto dává rozsah aktivace, takže to není binární aktivace. Určitě můžeme spojit několik neuronů dohromady a pokud se aktivuje více než 1, mohli bychom vzít maximum ( nebo softmax ) a rozhodnout se na jeho základě. Takže to je také v pořádku. V čem je tedy problém?“
Pokud znáte gradientní sestup pro trénování, všimli byste si, že pro tuto funkci je derivace konstantní.
A = cx, derivace vzhledem k x je c. To znamená, že gradient nemá žádný vztah k X. Je to konstantní gradient a sestup bude probíhat po konstantním gradientu. Pokud dojde k chybě v predikci, změny provedené zpětným šířením jsou konstantní a nezávisí na změně vstupu delta(x) !!!
To není tak dobré! ( Ne vždy, ale vydržte to se mnou ). Je tu i další problém. Zamyslete se nad propojenými vrstvami. Každá vrstva je aktivována lineární funkcí. Tato aktivace zase přechází do další vrstvy jako vstup a druhá vrstva na tomto vstupu vypočítá vážený součet a ten zase odpálí na základě další lineární aktivační funkce.
Nezáleží na tom, kolik vrstev máme, pokud jsou všechny lineární povahy, výsledná aktivační funkce poslední vrstvy není nic jiného než jen lineární funkce vstupu první vrstvy! Na chvíli se zastavte a přemýšlejte o tom.
To znamená, že tyto dvě vrstvy ( nebo N vrstev ) lze nahradit jedinou vrstvou. Aha! Tímto způsobem jsme právě přišli o možnost vrstvy stohovat. Nezáleží na tom, jak vrstvy poskládáme, celá síť je stále ekvivalentní jediné vrstvě s lineární aktivací ( kombinace lineárních funkcí lineárním způsobem je stále další lineární funkce ).
Pokračujme dál, ano?
Sigmoidní funkce
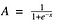
No, vypadá to hladce a „jako kroková funkce“. Jaké to má výhody? Chvíli se nad tím zamyslete. Za prvé, je to nelineární ve své podstatě. Kombinace této funkce jsou také nelineární! Skvělé. Nyní můžeme vrstvy skládat na sebe. A co nebinární aktivace? Ano, to také!. Na rozdíl od krokové funkce poskytne analogovou aktivaci. Má také hladký gradient.
A pokud si všimnete, mezi hodnotami X -2 až 2 jsou hodnoty Y velmi strmé. Což znamená, že jakákoli malá změna hodnot X v této oblasti způsobí výraznou změnu hodnot Y. Aha, to znamená, že tato funkce má tendenci přivádět hodnoty Y na oba konce křivky.
Vypadá to, že je vzhledem ke své vlastnosti dobrá pro klasifikátor? Ano! To skutečně je. Má tendenci přivádět aktivace na obě strany křivky ( například nad x = 2 a pod x = -2). Vytváří jasné rozdíly při predikci.
Další výhodou této aktivační funkce je, že na rozdíl od lineární funkce bude výstup aktivační funkce vždy v rozsahu (0,1) ve srovnání s (-inf, inf) lineární funkce. Máme tedy naše aktivace ohraničené v nějakém rozsahu. Pěkné, nebude to tedy aktivace nafukovat.
To je skvělé. Sigmoidní funkce jsou dnes jednou z nejpoužívanějších aktivačních funkcí. Jaké jsou s tím tedy problémy?“
Pokud si všimnete, směrem k oběma koncům sigmoidní funkce mají hodnoty Y tendenci reagovat velmi málo na změny v X. Co to znamená? Gradient v této oblasti bude malý. Vzniká tak problém „mizejícího gradientu“. Hmm. Co se tedy stane, když se aktivace dostanou do blízkosti „téměř vodorovné“ části křivky na obou stranách?“
Gradient je malý nebo zmizel ( nemůže provést významnou změnu kvůli extrémně malé hodnotě ). Síť se odmítá dále učit nebo je drasticky pomalá ( v závislosti na případu použití a dokud gradient / výpočet nenarazí na limity hodnot s plovoucí desetinnou čárkou ). Existují způsoby, jak tento problém obejít, a sigmoida je v klasifikačních problémech stále velmi oblíbená.
Funkce tanh
Další aktivační funkcí, která se používá, je funkce tanh.
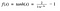
Hm. To vypadá velmi podobně jako sigmoida. Ve skutečnosti je to škálovaná sigmoidní funkce!“

Ok, tak tohle má podobné vlastnosti jako sigmoida, o které jsme mluvili výše. Je nelineární povahy, takže skvěle můžeme vrstvy skládat na sebe! Je vázána na rozsah (-1, 1), takže se nemusíme bát, že by aktivace vybuchla. Je třeba zmínit, že gradient je u tanh silnější než u sigmoid ( derivace jsou strmější). Rozhodování mezi sigmoidou a tanh bude záviset na vašich požadavcích na sílu gradientu. Stejně jako sigmoida má i tanh problém s mizejícím gradientem.
Tanh je také velmi oblíbená a široce používaná aktivační funkce.
ReLu
Později přichází funkce ReLu,
A(x) = max(0,x)
Funkce ReLu je taková, jak je uvedeno výše. Dává výstup x, pokud je x kladné, a 0 v opačném případě.
Na první pohled by se zdálo, že má stejné problémy jako lineární funkce, protože je lineární v kladné ose. ReLu je především nelineární ve své podstatě. A kombinace ReLu jsou také nelineární! ( Ve skutečnosti je to dobrý aproximátor. Jakoukoli funkci lze aproximovat kombinacemi ReLu). Skvělé, takže to znamená, že můžeme vrstvy skládat na sebe. Není to ale nijak vázané. Rozsah ReLu je [0, inf]. To znamená, že může aktivaci nafouknout.
Dalším bodem, který bych zde rád probral, je řídkost aktivace. Představte si velkou neuronovou síť se spoustou neuronů. Použití sigmoidy nebo tanh způsobí, že téměř všechny neurony budou hořet analogicky ( vzpomínáte? ). To znamená, že téměř všechny aktivace budou zpracovány pro popis výstupu sítě. Jinými slovy aktivace je hustá. To je nákladné. V ideálním případě bychom chtěli, aby se několik neuronů v síti neaktivovalo, a tím byly aktivace řídké a efektivní.
ReLu nám tuto výhodu poskytuje. Představte si síť s náhodně inicializovanými váhami ( nebo normalizovanou ) a téměř 50 % sítě dává aktivaci 0 kvůli charakteristice ReLu ( výstup 0 pro záporné hodnoty x ). To znamená, že střílí méně neuronů ( řídká aktivace ) a síť je lehčí. Pěkné! Zdá se, že ReLu je úžasný! Ano, je, ale nic není bezchybné.. Ani ReLu.
Vzhledem k vodorovné čáře v ReLu ( pro záporné X ) může gradient směřovat k 0. Pro aktivace v této oblasti ReLu bude gradient 0, kvůli čemuž se váhy během sestupu neupraví. To znamená, že ty neurony, které se dostanou do tohoto stavu, přestanou reagovat na změny chyby/vstupu ( jednoduše proto, že gradient je 0, nic se nemění ). Tomu se říká umírající problém ReLu. Tento problém může způsobit, že několik neuronů prostě odumře a nebude reagovat, čímž se podstatná část sítě stane pasivní. V ReLu existují varianty, jak tento problém zmírnit tím, že z vodorovné čáry jednoduše uděláte nevodorovnou složku . například y = 0,01x pro x<0 z ní udělá mírně nakloněnou čáru, nikoli vodorovnou. Jedná se o děravé ReLu. Existují i další varianty. Hlavní myšlenkou je nechat gradient nenulový a případně ho během trénování obnovit.
ReLu je výpočetně méně náročný než tanh a sigmoid, protože zahrnuje jednodušší matematické operace. To je dobré vzít v úvahu, když navrhujeme hluboké neuronové sítě.
Ok, kterou z nich teď použijeme?
Nyní, které aktivační funkce použít. Znamená to, že budeme na všechno používat jen ReLu? Nebo sigmoidu či tanh? No, ano i ne. Když víte, že funkce, kterou se snažíte aproximovat, má určité vlastnosti, můžete zvolit aktivační funkci, která bude funkci aproximovat rychleji, což povede k rychlejšímu procesu trénování. Například sigmoida dobře funguje pro klasifikátor ( viz graf sigmoidy, neukazuje vlastnosti ideálního klasifikátoru? ), protože aproximovat funkci klasifikátoru jako kombinaci sigmoidy je jednodušší než třeba ReLu. Což povede k rychlejšímu tréninkovému procesu a konvergenci. Můžete použít i své vlastní funkce!. Pokud neznáte povahu funkce, kterou se snažíte naučit, pak bych možná doporučil začít s ReLu a pak pracovat zpětně. ReLu většinou funguje jako obecný aproximátor!“
V tomto článku jsem se pokusil popsat několik běžně používaných aktivačních funkcí. Existují i jiné aktivační funkce, ale obecná myšlenka zůstává stejná. Výzkum lepších aktivačních funkcí stále probíhá. Doufám, že jste pochopili, co se skrývá za aktivačními funkcemi, proč se používají a jak se rozhodujeme, kterou z nich použít
.