Lotka-Volterrovy rovnice popisují ekologický model predátor-kořist (nebo parazit-hostitel), který předpokládá, že, pro soubor pevných kladných konstant 
(rychlost růstu kořisti), 
(rychlost, s níž predátoři ničí kořist), 
(rychlost úmrtí predátorů) a 
(rychlost, s níž predátoři přibývají konzumací kořisti) platí následující podmínky.
1. Populace kořisti 
se zvětšuje rychlostí 
(úměrnou počtu kořisti), ale současně je ničena predátory rychlostí 
(úměrnou součinu počtu kořisti a predátorů).
2. Populace predátorů 
klesá rychlostí 
(úměrnou počtu predátorů), ale roste rychlostí 
(opět úměrnou součinu počtu kořisti a predátorů).
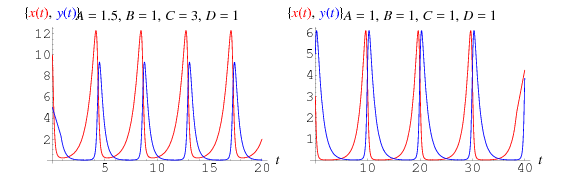
Tím získáme spřažené diferenciální rovnice
 |
 |
 |
(1)
|
 |
 |
 |
(2)
|
jejichž řešení jsou vynesena výše, kde kořist je znázorněna červeně a predátoři modře. V tomto druhu modelu vede křivka kořisti vždy před křivkou predátorů.
Kritické body nastávají, když 
, takže
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
Jediný stacionární bod se tedy nachází v bodě 
.