Jaký je rozdíl mezi konkávním a konvexním tvarem?
Pokud bychom měli co nejobecněji popsat rozdíl mezi konkávním a konvexním tvarem, řekli bychom, že jakýkoli dutý předmět podobný misce je konkávní, zatímco jakýkoli předmět připomínající ragbyový nebo fotbalový míč má konvexní tvar. Důvodem, proč se konvexní a konkávní tvar tak často nesprávně používají, je však možná to, že tato dvě slova nejsou tak jednoduchá, jak bychom si přáli.
Většina gramatických zdrojů trvá na tom, jak je možné pomocí mnemotechniky rozluštit konvexní a konkávní pomocí slova jeskyně. Zatímco představa spojování konkávního s událostí, kdy se něco „propadne“, pomáhá učit se o vlastnostech povrchu, je matoucí vztahovat tuto představu k předmětům zahrnujícím grafy.
Abychom pochopili, jak se od sebe konkávní a konvexní liší, musíme se naučit, jak se každý z termínů používá v kapacitě matematiky, zrcadel, čoček a konečně v rámci tvůrčího psaní. Jakmile se rozhodnete, v jakém kontextu chcete slova jako konkávní a konvexní používat, seznámení s jejich technickými aspekty vám umožní být si jistější při jejich používání v běžné řeči.

Co znamená slovo konkávní
Konkávní se používá jako přídavné nebo podstatné jméno k popisu tvaru předmětu nebo povrchu, který je zahnutý dovnitř nebo vydutý jako mísa. Příklady použití slova concave ve větě:
„Nabrala zmrzlinu z nádoby a zanechala po sobě konkávní stopu.“
Podle Oxfordského slovníku historických slov slovo concave pochází z pozdní střední angličtiny. Konkávní a konkávní vytváří latinský termín concavus (con- a cavus), který se překládá jako „spolu“ a „dutý“ („Concave“, 110).
Mezi synonyma slova concave patří např:
Dented, depressed, dished, hollow, indented, recessed, and sunken.
Antonymy slova concave (konkávní) zahrnují:
Vyklenutý, vyklenutý, vyčnívající, vystouplý, vystouplý.
Co znamená slovo konvexní?
Slovo konvexní neboli vypouklý je přídavné jméno popisující předmět nebo povrch, který je zaoblený nebo zakřivený. Pokud jde o předměty, je střední plocha konvexního předmětu širší než jeho vnější roh. Příklady vypouklého tvaru ve větě:
„Spadl jsem do jedovatého břečťanu a teď mám po celé kůži červené, vypouklé boule.“
Mezi synonyma vypouklého patří např:
Vyklenutý, ohnutý, vypouklý, vyvýšený.
Antonymy slova konvexní zahrnují:
Vyklenutý, ohnutý, vypouklý, vyvýšený:
Vyklenutý, klesající.
Konkávní vs. konvexní funkce
Konvexní funkce představuje spojitou čáru na grafu, kde střed neboli střední celé číslo oboru nepřesahuje střední hodnotu intervalu. Konkávní funkce je přesným opakem konvexní funkce, protože aby byla funkce f(x) konkávní, musí být f(x) záporná. Abychom si rozdíly ujasnili, uvádíme rychlý přehled srovnání těchto pojmů:
Konkávní směrem nahoru = konvexní = konvexní směrem dolů
Konkávní směrem dolů = konkávní = konvexní směrem nahoru
Rozdíl mezi konkávní a konvexní funkcí si názorněji ukážeme, když se podíváme na graf. Všimněte si, jak se konvexní funkce otevírá směrem nahoru, zatímco konkávní funkce směrem dolů.
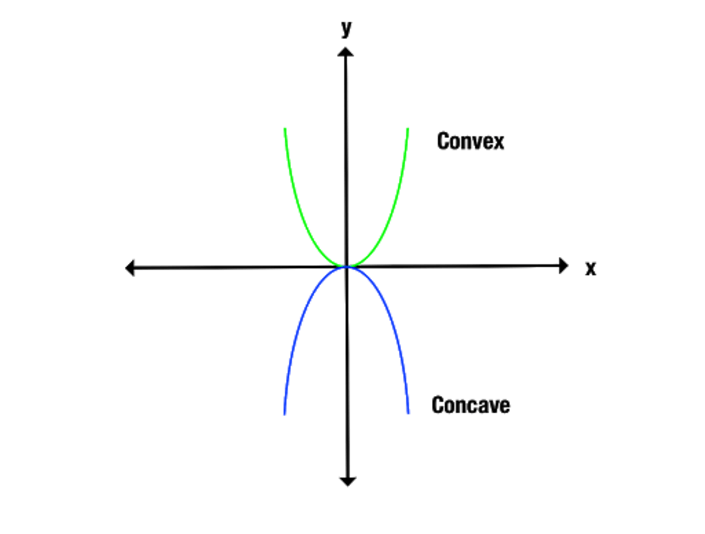
Jiným způsobem, jak rozpoznat konkávní a konvexní funkci, je spojit body na grafu podél osy x. V grafu se zobrazují body, které jsou konvexní. Konkávní funkce spojuje pouze přímky pod grafem, zatímco konvexní funkce vytváří pouze přímky nad grafem.
K rozluštění toho, zda je funkce konvexní nebo konkávní, můžeme navíc použít výpočet. Pokud je druhá derivace funkce f(x) větší než nula, pak je funkce konvexní. Pokud je však druhá derivace funkce f(x) menší než nula, je funkce konkávní.
Konvexní vs. konkávní mnohoúhelníky
Nepropadejte panice, ale slova konvexní a konkávní se používají i v geometrii. O konvexních a konkávních útvarech se nejčastěji hovoří v souvislosti s mnohoúhelníky, což jsou útvary s minimálně třemi stranami a úhly.
Pravidelné mnohoúhelníky existují se stejnými stranami a úhly, ale konvexní a konkávní mnohoúhelníky jsou trochu složitější. Konvexní mnohoúhelníky obsahují vnitřní úhly, které jsou menší než 180 stupňů, zatímco konkávní mnohoúhelníky obsahují jeden nebo více vnitřních úhlů, které jsou větší než 180 stupňů.
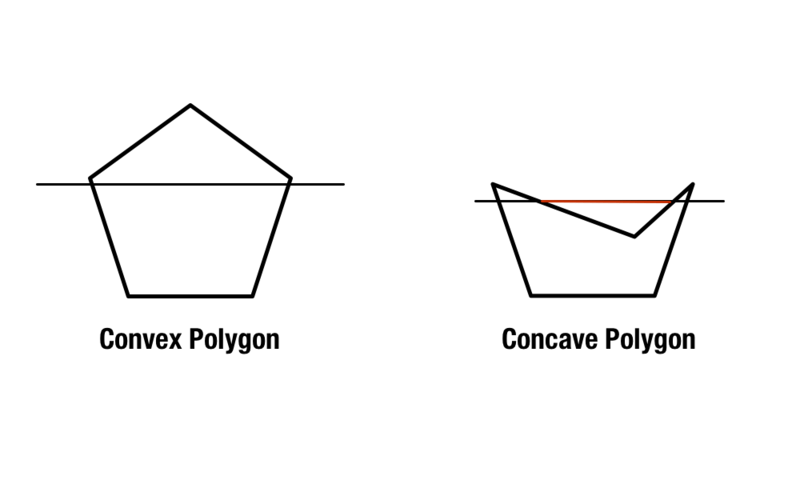
Druhou metodou identifikace konkávních a konvexních mnohoúhelníků je nakreslení dvou úhlopříček napříč útvarem, které vycházejí z jeho rohů. Pokud každá čára existuje uvnitř útvaru, je útvar konvexní. Pokud existuje alespoň jedna přímka, která prochází mimo útvar, je útvar konkávní.
Konkávní vs. konvexní zrcadla
Slova konkávní a konvexní se běžně používají při diskusi o optických objektech, jako jsou zrcadla a čočky. Jakákoli konvexní plocha vystupuje směrem ven, podobně jako bublina, což vyvolává efekt šířky. Konvexní zrcadla se běžně vyskytují v parkovacích garážích, kde řidiči potřebují široký výhled za roh nebo do potenciálních mrtvých úhlů.

Konkávní zrcadlo je naopak zakřivené dovnitř a vytváří zvětšený odraz, který je obráceně. Jak ukázali vědci z University of South Wales’s School of Physics, každý, kdo má lesklou lžíci, si může toto pozorování ověřit tak, že se podívá na svůj odraz ve lžíci. Na konkávním povrchu lžíce, kde nabíráte jídlo, se váš odraz úzce zkreslí a vy se budete jevit vzhůru nohama. Pokud však lžíci otočíte na vypouklou stranu, váš odraz bude vzpřímený a menší.
Odrazy se tak výrazně liší mezi konvexními a konkávními povrchy, protože bez ohledu na to, zda je povrch zakřivený směrem ven nebo dovnitř, je zrcadlo samo o sobě součástí koule. Protože povrch koule není plochý, světlo odražené od jejího povrchu urazí různou vzdálenost, než se dotkne zrcadla.
V závislosti na tom, se kterou částí povrchu se světlo dotkne, se může paprsek světla odrazit od okolních povrchů a vytvořit tak soustředěnější oblast viditelnosti. To je důvod, proč při pohledu na vnitřní povrch lžíce můžeme vidět pouze odraz toho, co je nejblíže povrchu lžíce – i když se stále zdá menší. Navíc, pokud byste dovnitř lžíce položili prst, může povrch zrcadla vytvářet dva nebo tři různé odrazy najednou.
Konkávní čočka vs. konvexní čočka
Konkávní a konvexní čočky existují v předmětech denní potřeby, jako jsou brýle, kontaktní čočky, dalekohledy a teleskopy. Podobně jako vědecké poznatky o odrazu světla na konvexních a konkávních zrcadlech, existují i zákonitosti pro to, jak světlo prochází konkávními a konvexními čočkami a vytváří viditelný obraz.

Konvexní čočky
Podle Manochovy akademie se konvexní čočky nazývají sbíhavé čočky, protože mají schopnost vytvářet obrazy zmenšené, zvětšené nebo introvertní. To, jak přesně se obraz skrze konvexní čočku zobrazí, závisí na tom, jak blízko je předmět k ohnisku čočky. U každé konvexní čočky jsou na obou stranách čočky symetrická ohniska.
Jak přesně se předmět zobrazí přes konvexní čočku, lze předpovědět pomocí tří principů:
Princip 1: Každý světelný paprsek, který prochází konvexní čočkou, je rovnoběžný s hlavní osou, což je středová přímka procházející absolutním středem sférické čočky. Jakmile se světlo dotkne čočky, láme se a prochází ohniskem na druhé straně. Procházející světelné paprsky, které jsou rovnoběžné s hlavní osou, se pohybují nad předmětem před čočkou.
Princip 2: Každý světelný paprsek, který projde středem konvexní čočky, bude na druhé straně pokračovat v přímce.
Princip 3: Každý paprsek světla, který prošel ohniskem na stejné straně jako předmět, se při dotyku s čočkou zalomí a na druhé straně se stane rovnoběžným s hlavní osou.
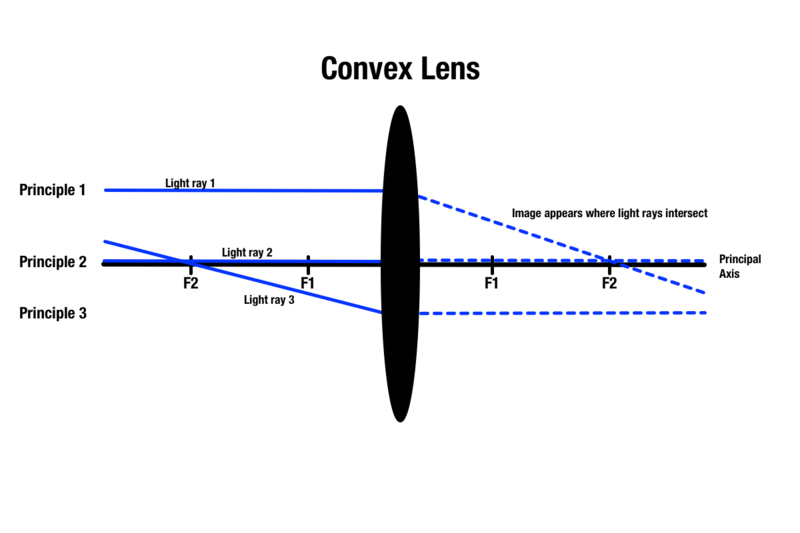
Přestože existují tři principy pro předpověď kvality obrazu přes konvexní čočku, při kreslení paprskového diagramu lze na předmět použít pouze dva principy. Kterékoli dva principy vytvoří průsečík světla na druhé straně čočky, který označí oblast, kde se objeví obraz předmětu.
Čím dále je předmět od vypuklé čočky, tím menší bude obraz na druhé straně, a čím blíže je předmět vypuklé čočce, tím větší se bude jevit. Objekt, který se nachází za nejbližším ohniskem, vytváří větší obraz za objektem. Jak upozorňuje Manocha Academy, tento typ zvětšovací čočky se používá u optických pomůcek, jako jsou lupy.
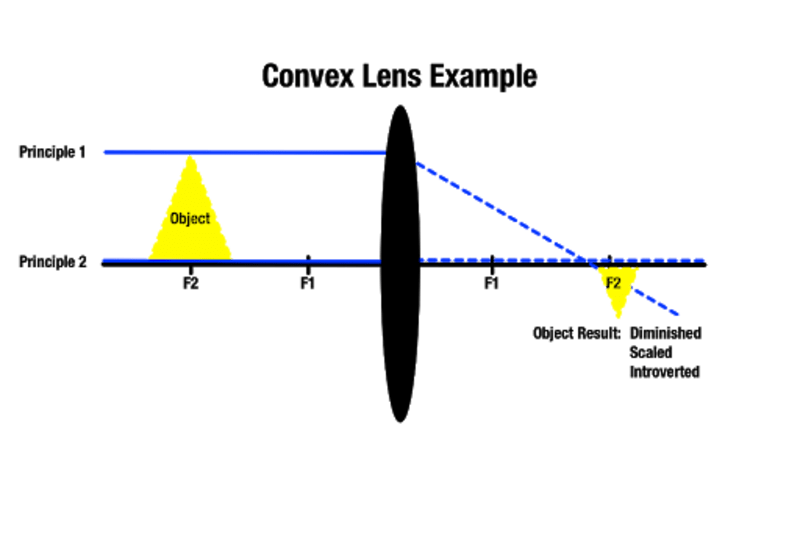
V závislosti na tom, ve kterém ohnisku se předmět nachází, je možné vytvořit obraz, který má přibližnou velikost. Je také možné vytvořit skutečné obrazy, které nejsou viditelné, pokud se procházející světelné paprsky nikdy neprotnou, protože jsou na druhé straně rovnoběžné. V tomto případě existuje vytvořený obraz v nekonečné vzdálenosti.
Konkávní čočky
Každá konkávní čočka bude mít silnější průměr a tenčí střed, protože konkávní čočka je zakřivená dovnitř. Tvar konkávních čoček umožňuje, aby se světlo po kontaktu s čočkou rozptýlilo, díky čemuž se virtuální objekty zdají menší. Schopnost konkávní čočky rozprostřít světlo z ní činí ideální čočku pro nástroje, jako jsou svítilny, kde lze použít centrální zdroj světla na větší ploše.
Konkávní čočky vytvářejí obraz pomocí tří principů, které jsou podobné konvexním čočkám:
Princip 1: Jakýkoli světelný paprsek, který se pohybuje nad předmětem a je rovnoběžný s hlavní osou, se při kontaktu s čočkou láme a vypadá, jako by přicházel ze směru nejbližšího ohniska.
Princip 2: Každý paprsek světla procházející středem konkávní čočky projde bez lomu.
Princip 3: Jakýkoli paprsek světla směřující do ohniska na druhé straně konkávní čočky se bude lámat a stane se rovnoběžným s hlavní osou.
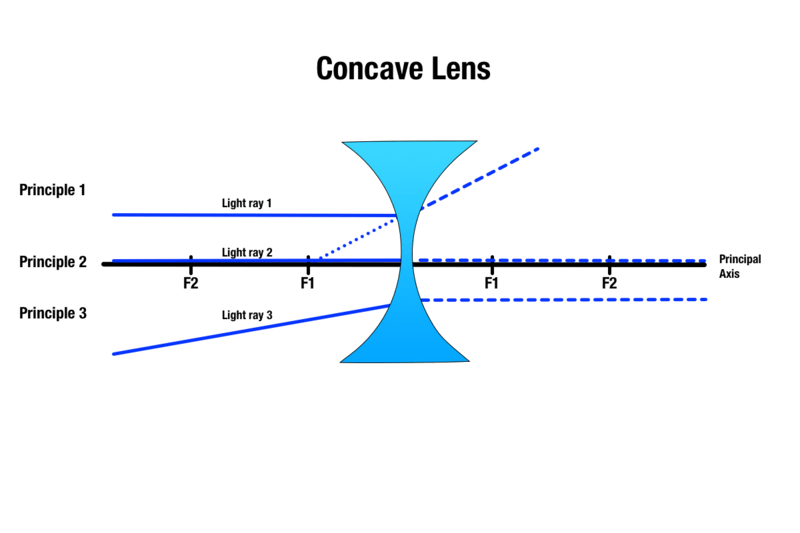
Ačkoli se velikost obrazu předmětu mění v závislosti na vzdálenosti předmětu od konkávní čočky, vytvořený obraz je vždy virtuální, vzpřímený, menší a objevuje se na stejné straně čočky jako předmět.
Konkávní vs. konvexní v písmu
Slova konkávní a konvexní jsou protikladná a v podstatě popisují tvar předmětů nebo povrchů stejným způsobem, jakým stavíme do protikladu slova jako:
- Malý vs. malý. velký
- Vysoký vs. krátký
- Tenký vs. široký
- Kulatý vs. plochý
Protože konkávní a konvexní jsou odborná slova, jejich popisné použití v próze může u běžného publika vyvolat spíše metaforický nebo abstraktní výklad. To znamená, že pokud se spisovatelé rozhodnou použít konkávní nebo konvexní mimo oblast jejich typického použití, musí se rozhodnout, jak jednoznačné má být jejich psaní.
Zvažte přídavné jméno
Významným příkladem použití konkávního nebo konvexního v literatuře jsou texty amerického spisovatele Davida Fostera Wallace (zkráceně DFW). DFW je proslulý svým složitým a odborným stylem psaní – a ano, několikrát použil konvexní a konkávní k popisu podstatných jmen. Wallace používá konkávní a konvexní v následujících příkladech:
„Můj pohled na ruce byl v pořádku, ale nebyl jsem ani velký, ani rychlý, měl jsem téměř konkávní hrudník a zápěstí tak tenká, že jsem si je mohl vzít do náramku palcem a malíčkem…“.
– „Tenis, trigonometrie, tornáda: „A Midwestern Boyhood“, Harper’s Magazine.
„…panenkovské oči, které se otevírají tahem srdeční struny, konkávní tam, kde jsem já konvexní.“
– „Order and Flux in Northampton,“ Conjunctions.
Smyslem použití příkladů DFW není pouze ukázat, jak spisovatelé použili konvexní nebo konkávní mimo matematický kontext, ale spíše to, aby spisovatelé zvážili, zda je použití technických nebo abstraktních termínů užitečné pro jasné sdělení jejich publiku.
V prvním příkladu DFW dává použití konkávního výrazu smysl, protože popisuje strukturu něčeho. Používání konkávních a konvexních výrazů k popisu neobjektivních podstatných jmen, jako jsou pocity nebo myšlenky, však má tendenci zastírat význam toho, co se snažíme vysvětlit. Druhý příklad DFW se pohybuje na tenké hranici při používání konvexních a konkávních, protože jejich použití je jak doslovné, tak metaforické.
FAQ:
Co je to funkce?
Funkce je rovnice přímky na grafu. Funkce jsou pro každou přímku na grafu jiné, ale mají obecný tvar,
f(x) = x + 1
U každé přímkové funkce je závislá proměnná obvykle f(x), zatímco každá neznámá proměnná v rámci funkce se nazývá nezávislá proměnná.
Co je to obor?“
Obor je množina nezávislých proměnných na grafu, která odpovídá funkci přímky. Domény je důležité pochopit, protože lokalizují konkrétní body na grafu, které odpovídají jakémukoli reálnému výstupu rovnice.
Co je to rozsah?“
Obsah jakékoli funkce představuje jakoukoli možnou hodnotu podél osy x nebo y na grafu, která dává platnou hodnotu závislé proměnné. Všechna minima a maxima celých hodnot jsou určena náhradou proměnných za osy x nebo y.
Co je to interval?
Interval je množina čísel, která představují celá čísla přímky, tzv. doménu. Uzavřený interval zahrnuje dva konečné body přímky, kde mimo obor celých čísel již přímka neexistuje. Otevřený interval je množina celých čísel, která nepředstavují absolutní konec oboru přímky.
Vyzkoušejte se!“
Zjistěte, jak dobře rozumíte rozdílu mezi konvexitou a konkávou, pomocí následujících otázek s výběrem odpovědi:
- Při pohledu na lesklou lžíci si všimnete, že váš odraz je obráceně. Povrch lžíce je _________povrch.
a. Konvexní
b. Zrcadlo
c. Konkávní
d. Kovová - Z hlediska grafického znázornění funkcí se někdy konvexní funkce nazývá:
a. Konkávní směrem nahoru
b. Konvexní směrem dolů
c. Konkávní směrem dolů
d. A a B - Která z následujících možností nepopisuje konkávní plochu:
a. Dutá polokoule
b. Oční čočka
c. Miska na cereálie
d. Polokoule - Která z následujících možností nepopisuje konvexní povrch:
a. Postava Stewieho ze seriálu Family Guy
b. Koule
c. Zrcadlo v garáži
d. Fotbalový míč - Který z následujících útvarů nemůže existovat jako konkávní mnohoúhelník:
a. Pentagon
b. Šestiúhelník
c. Trojúhelník
d. Osmiúhelník
Odpovědi
- C: Konkávní
- D: A a B
- D: Polokoule
- B: Koule
- C: Trojúhelník
Zdroje:
- Bourne, M. „Domain and Range of a Function“. Interaktivní matematika, 4. 1. 2019.
- „Konkávní“. Merriam-Webster Dictionary, 2019.
- „Konkávní“. Oxfordský slovník historických slov, vyd. Chantrell, 2002, s. 110.
- „Konkávní a konvexní zrcadla“. Manocha Academy, YouTube, 2019.
- „Konkávní čočka: Definice & Použití“. Study.com, 2019.
- „Konvexní zrcadlo“. Merriam-Webster Dictionary, 2019.
- „Konvexní a konkávní čočky“. Manocha Academy, YouTube, 2019.
- „Matematika / Porozumění mnohoúhelníkům“. Learnhive Inc.“, 2018.
- „Odraz od konkávního zrcadla“. UNSW Physics, YouTube, 2017.
- Wallace, D.F. „Tenis, trigonometrie, tornáda: A Midwestern Boyhood.“ Harper’s Magazine, 1991.
- Wallace, D.F. „Order and Flux in Northampton“ (Řád a proudění v Northamptonu). Conjunctions, 1991.
- Weisstein, Eric W. „Concave Function.“ (Konkávní funkce). MathWorld-A Wolfram Web Resource, b.d.
- Weisstein, Eric W. „Convex Function“. MathWorld-A Wolfram Web Resource, b.d.
The Word Counter je dynamický online nástroj sloužící k počítání slov, znaků, vět, odstavců a stránek v reálném čase spolu s kontrolou pravopisu a gramatiky.