Když jsou data připravena k analýze, mělo by být na základě kontroly dat důkladně posouzeno, zda by měly být použity statistické metody pro zpracování chybějících údajů. Bell a kol. se zaměřili na posouzení rozsahu a způsobu zpracování chybějících údajů v randomizovaných klinických studiích publikovaných od července do prosince 2013 v časopisech BMJ, JAMA, Lancet a New England Journal of Medicine . V 95 % ze 77 identifikovaných studií byly uvedeny některé chybějící údaje o výsledcích. Nejčastěji používanou metodou zpracování chybějících údajů v primární analýze byla analýza úplných případů (45 %), jednoduchá imputace (27 %), metody založené na modelu (například smíšené modely nebo zobecněné odhadovací rovnice) (19 %) a vícenásobná imputace (8 %) .
Analýza úplných případů
Analýza úplných případů je statistická analýza založená na účastnících s úplným souborem výsledných údajů. Účastníci s jakýmikoliv chybějícími údaji jsou z analýzy vyloučeni. Jak je popsáno v úvodu, pokud jsou chybějící údaje MCAR, bude mít analýza úplných případů sníženou statistickou sílu kvůli zmenšené velikosti vzorku, ale pozorované údaje nebudou zkreslené . Pokud chybějící údaje nejsou MCAR, může být odhad účinku intervence v analýze úplných případů založen, tj. často bude existovat riziko nadhodnocení přínosu a podhodnocení újmy . Podrobnější diskusi o potenciální platnosti v případě použití úplné případové analýzy naleznete v části „Měla by se pro zpracování chybějících údajů použít vícenásobná imputace?“
Jednorázová imputace
Při použití jednorázové imputace se chybějící hodnoty nahradí hodnotou definovanou určitým pravidlem . Existuje mnoho forem jednoduché imputace, například přenesení posledního pozorování (chybějící hodnoty účastníka jsou nahrazeny poslední pozorovanou hodnotou účastníka), přenesení nejhoršího pozorování (chybějící hodnoty účastníka jsou nahrazeny nejhorší pozorovanou hodnotou účastníka) a prostá imputace průměru . Při prosté imputaci průměru jsou chybějící hodnoty nahrazeny průměrem pro danou proměnnou . Použití jednoduché imputace často vede k podhodnocení variability, protože každá nepozorovaná hodnota má v analýze stejnou váhu jako známé, pozorované hodnoty . Platnost jednoduché imputace nezávisí na tom, zda jsou údaje MCAR; jednoduchá imputace spíše závisí na specifických předpokladech, že chybějící hodnoty jsou například totožné s poslední pozorovanou hodnotou . Tyto předpoklady jsou často nereálné, a proto je jednoduchá imputace často potenciálně neobjektivní metodou a měla by se používat s velkou opatrností .
Vícená imputace
Vícená imputace se ukázala jako platná obecná metoda pro zpracování chybějících údajů v randomizovaných klinických studiích a tato metoda je k dispozici pro většinu typů údajů . V následujících částech popíšeme, kdy a jak by měla být vícenásobná imputace použita.
Měla by být vícenásobná imputace použita pro zpracování chybějících údajů?
Důvody, proč by vícenásobná imputace neměla být použita pro zpracování chybějících údajů
Je platné ignorovat chybějící údaje?
Analýza pozorovaných údajů (analýza úplných případů) ignorující chybějící údaje je platným řešením za tří okolností.
- a)
Analýzu úplných případů lze použít jako primární analýzu, pokud je podíl chybějících údajů nižší než přibližně 5 % (jako pravidlo) a je nepravděpodobné, že určité skupiny pacientů (například velmi nemocní nebo velmi „zdraví“ účastníci) jsou specificky ztraceni pro sledování v jedné ze srovnávaných skupin . Jinými slovy, pokud je potenciální dopad chybějících údajů zanedbatelný, lze chybějící údaje v analýze ignorovat . V případě pochybností lze použít analýzy citlivosti pro nejlepší a nejhorší případ: nejprve se vytvoří soubor údajů pro „nejlepší a nejhorší případ“, kde se předpokládá, že všichni účastníci ztracení do sledování v jedné skupině (označované jako skupina 1) měli příznivý výsledek (například neměli žádnou závažnou nežádoucí příhodu); a všichni účastníci s chybějícími výsledky v druhé skupině (skupina 2) měli škodlivý výsledek (například měli závažnou nežádoucí příhodu) . Poté se vytvoří soubor údajů pro „nejhorší možný scénář“, u něhož se předpokládá, že všichni účastníci ztracení při sledování ve skupině 1 měli škodlivý výsledek; a že všichni účastníci ztracení při sledování ve skupině 2 měli příznivý výsledek . Pokud se použijí spojité výsledky, pak „příznivý výsledek“ může být průměr skupiny plus 2 směrodatné odchylky (nebo 1 směrodatná odchylka) od průměru skupiny a „škodlivý výsledek“ může být průměr skupiny minus 2 směrodatné odchylky (nebo 1 směrodatná odchylka) od průměru skupiny . U dichotomizovaných údajů pak tyto analýzy citlivosti pro nejlepší a nejhorší případ ukáží rozsah nejistoty v důsledku chybějících údajů, a pokud tento rozsah nedává kvalitativně protichůdné výsledky, lze chybějící údaje ignorovat. U spojitých údajů bude imputace s 2 SD představovat možný rozsah nejistoty vzhledem k 95 % pozorovaných údajů (pokud jsou normálně rozděleny).
- b)
Pokud má chybějící hodnoty pouze závislá proměnná a pomocné proměnné (proměnné, které nejsou zahrnuty do regresní analýzy, ale korelují s proměnnou s chybějícími hodnotami a/nebo souvisejí s její chybějící hodnotou) nejsou identifikovány, lze jako primární analýzu použít analýzu úplných případů a pro zpracování chybějících údajů by se neměly používat žádné zvláštní metody . Žádné další informace se nezískají například použitím vícenásobné imputace, ale standardní chyby se mohou zvýšit v důsledku nejistoty vnesené vícenásobnou imputací .
- c)
Jak bylo uvedeno výše (viz Metody zpracování chybějících údajů), platilo by také pouze provést analýzu úplných případů, pokud je relativně jisté, že údaje jsou MCAR (viz Úvod). Je poměrně vzácné, aby bylo jisté, že údaje jsou MCAR. Je možné testovat hypotézu, že data jsou MCAR, pomocí Littleova testu , ale může být nerozumné stavět na testech, které se ukázaly jako nevýznamné. Proto pokud existují důvodné pochybnosti, zda jsou data MCAR, i když je Littleův test nevýznamný (nepodaří se zamítnout nulovou hypotézu, že data jsou MCAR), nemělo by se předpokládat, že se jedná o MCAR.
Jsou podíly chybějících dat příliš velké?“
Pokud chybí velké podíly dat, mělo by se zvážit, zda stačí uvést výsledky úplné analýzy případů a poté jasně diskutovat o výsledných interpretačních omezeních výsledků studie. Pokud se pro zpracování chybějících údajů použije vícenásobná imputace nebo jiné metody, může to znamenat, že výsledky studie jsou potvrzující, což v případě značného chybění nejsou. Pokud jsou podíly chybějících údajů u důležitých proměnných velmi velké (například více než 40 %), lze výsledky studie považovat pouze za výsledky vytvářející hypotézu . Vzácnou výjimkou by bylo, pokud lze základní mechanismus chybějících údajů popsat jako MCAR (viz odstavec výše).
Připadá vám předpoklad MCAR i MAR nevěrohodný?
Pokud se předpoklad MAR jeví na základě charakteristik chybějících údajů jako nevěrohodný, pak budou výsledky studie vystaveny riziku zkreslení výsledků v důsledku „zkreslení neúplných výsledných údajů“ a žádná statistická metoda nemůže s jistotou toto potenciální zkreslení zohlednit . Platnost metod používaných pro zpracování údajů MNAR vyžaduje určité předpoklady, které nelze testovat na základě pozorovaných údajů. Analýzy citlivosti pro nejlepší a nejhorší případ mohou ukázat celý teoretický rozsah nejistoty a závěry by měly být vztaženy k tomuto rozsahu nejistoty. Omezení analýz by měla být důkladně prodiskutována a zvážena.
Je výsledná proměnná s chybějícími hodnotami spojitá a analytický model komplikovaný (např. s interakcemi)?
V této situaci lze zvážit použití přímé metody maximální věrohodnosti, aby se předešlo problémům s kompatibilitou modelu mezi analytickým modelem a modelem vícenásobné imputace, kdy první z nich je obecnější než druhý. Obecně lze použít přímé metody maximální věrohodnosti, ale pokud je nám známo, komerčně dostupné metody jsou v současné době k dispozici pouze pro spojité proměnné.
Kdy a jak použít vícenásobnou imputaci
Pokud není splněn žádný z výše uvedených „Důvodů, proč by se vícenásobná imputace neměla používat ke zpracování chybějících údajů“, pak by se vícenásobná imputace mohla použít. V literatuře byly v posledních několika desetiletích navrženy různé postupy pro řešení chybějících údajů . Výše uvedené úvahy o statistických metodách pro zpracování chybějících údajů jsme nastínili na obr. 1.
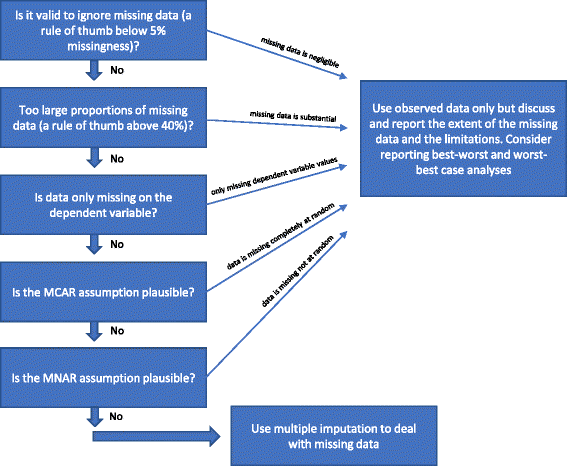
Květový diagram: Kdy je třeba použít vícenásobnou imputaci ke zpracování chybějících údajů při analýze výsledků randomizovaných klinických studií
Vícená imputace vznikla na počátku 70. let 20. století a v průběhu let získala stále větší popularitu . Vícenásobná imputace je statistická technika založená na simulaci pro zpracování chybějících údajů . Vícenásobná imputace se skládá ze tří kroků:
-
Krok imputace. Imputace“ obecně představuje jednu sadu věrohodných hodnot chybějících údajů – vícenásobná imputace představuje více sad věrohodných hodnot . Při použití vícenásobné imputace jsou chybějící hodnoty identifikovány a nahrazeny náhodným vzorkem věrohodných hodnot imputací (doplněných souborů dat). Vícenásobné doplněné soubory dat jsou generovány prostřednictvím některého zvoleného modelu imputace . Z teoretických důvodů se tradičně navrhuje jako dostačující pět imputovaných souborů dat, ale 50 (nebo více) souborů dat se zdá být vhodnější, aby se snížila výběrová variabilita procesu imputace .
-
Krok analýzy (odhadu) dokončených dat. Požadovaná analýza se provádí zvlášť pro každý soubor údajů, který je generován během kroku imputace . Tímto způsobem je zkonstruováno například 50 výsledků analýzy.
-
Krok sdružování. Výsledky získané z každé dokončené analýzy dat se spojí do jednoho výsledku vícenásobné imputace . Není třeba provádět váženou metaanalýzu, protože se má za to, že všech řekněme 50 výsledků analýzy má stejnou statistickou váhu.
Je velmi důležité, aby mezi modelem imputace a modelem analýzy existovala kompatibilita nebo aby model imputace byl obecnější než model analýzy (například aby model imputace zahrnoval více nezávislých kovariát než model analýzy) . Například pokud model analýzy obsahuje významné interakce, pak by je měl imputační model zahrnovat také , pokud model analýzy používá transformovanou verzi proměnné, pak by měl imputační model používat stejnou transformaci atd.
Existují různé typy vícenásobné imputace
Různé typy metod vícenásobné imputace. Uvedeme je podle jejich rostoucího stupně složitosti: 1) regresní analýza s jednou hodnotou; 2) monotónní imputace; 3) zřetězené rovnice nebo metoda Markovova řetězce Monte Carlo (MCMC). V následujících odstavcích popíšeme tyto různé metody vícenásobné imputace a způsob volby mezi nimi.
Regresní analýza s jednou proměnnou zahrnuje závislou proměnnou a stratifikační proměnné použité při náhodném výběru. Stratifikační proměnné často zahrnují indikátor centra, pokud se jedná o multicentrickou studii, a obvykle jednu nebo více nastavovacích proměnných s prognostickou informací, které korelují s výsledkem. Při použití spojité závislé proměnné může být zahrnuta také výchozí hodnota závislé proměnné. Jak je uvedeno v části „Důvody, proč by se neměly používat statistické metody pro zpracování chybějících údajů“, pokud chybí pouze hodnoty závislé proměnné a pomocné proměnné nejsou identifikovány, měla by se provést úplná analýza případu a neměly by se používat žádné zvláštní metody pro zpracování chybějících údajů . Pokud byly pomocné proměnné identifikovány, lze provést imputaci jedné proměnné. Pokud jsou u základní proměnné spojité proměnné významné chybějící údaje, může úplná analýza případů poskytnout zkreslené výsledky . Proto se ve všech případech provádí imputace jedné proměnné (podle potřeby se zahrnutím pomocných proměnných nebo bez nich), pokud chybí pouze základní proměnná.
Pokud chybí závislá i základní proměnná a chybění je monotónní, provádí se monotónní imputace. Předpokládejme datovou matici, kde pacienti jsou reprezentováni řádky a proměnné sloupci. O chybějící hodnotě takové datové matice se říká, že je monotónní, jestliže její sloupce lze uspořádat tak, že pro kteréhokoli pacienta (a) pokud hodnota chybí, všechny hodnoty napravo od její pozice jsou také chybějící, a (b) pokud je hodnota sledovaná, všechny hodnoty nalevo od této hodnoty jsou také sledované . Pokud je chybějící hodnota monotónní, je metoda vícenásobné imputace rovněž poměrně jednoduchá, a to i v případě, že chybí hodnoty více než jedné proměnné . V tomto případě je poměrně jednoduché chybějící údaje imputovat pomocí sekvenční regresní imputace, kdy se chybějící hodnoty imputují pro každou proměnnou najednou . Mnoho statistických balíků (například STATA) může analyzovat, zda je chybějící hodnota monotónní či nikoliv.
Pokud chybějící hodnota není monotónní, provádí se vícenásobná imputace pomocí zřetězených rovnic nebo metody MCMC. Pomocné proměnné jsou do modelu zahrnuty, pokud jsou k dispozici. Způsob volby mezi různými metodami vícenásobné imputace jsme shrnuli na obr. 2.
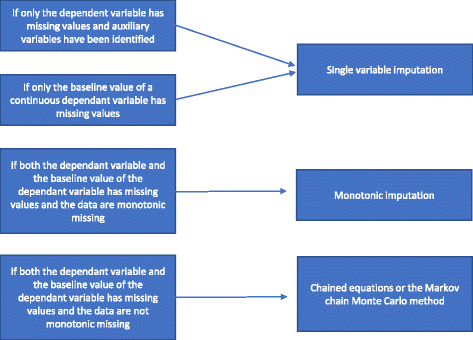
Květový diagram vícenásobné imputace
Plná informační maximální věrohodnost
Plná informační maximální věrohodnost je alternativní metoda pro řešení chybějících údajů . Principem odhadu maximální věrohodnosti je odhadnout parametry společného rozdělení výsledku (Y) a kovariát (X1,…, Xk), které, pokud by byly pravdivé, by maximalizovaly pravděpodobnost pozorování hodnot, které jsme ve skutečnosti pozorovali . Pokud u daného pacienta hodnoty chybí, můžeme pravděpodobnost získat součtem obvyklé pravděpodobnosti nad všemi možnými hodnotami chybějících údajů za předpokladu, že mechanismus chybějících údajů je ignorovatelný. Tato metoda se označuje jako plná informační maximální věrohodnost .
Plná informační maximální věrohodnost má ve srovnání s vícenásobnou imputací silné stránky i omezení.
Silné stránky plné informační maximální věrohodnosti ve srovnání s vícenásobnou imputací
- 1)
Je jednodušší na implementaci, tj. není nutné procházet různými kroky jako při použití vícenásobné imputace.
- 2)
Na rozdíl od vícenásobné imputace nemá plná informační maximální věrohodnost žádné potenciální problémy s neslučitelností mezi modelem imputace a modelem analýzy (viz „Vícenásobná imputace“). Platnost výsledků vícenásobné imputace bude sporná, pokud existuje neslučitelnost mezi modelem imputace a modelem analýzy nebo pokud je model imputace méně obecný než model analýzy .
- 3)
Při použití vícenásobné imputace jsou všechny chybějící hodnoty v každém generovaném souboru dat (imputační krok) nahrazeny náhodným vzorkem věrohodných hodnot . Proto, pokud není zadán „náhodný vzorek“, budou při každém provedení analýzy vícenásobné imputace zobrazeny jiné výsledky . Analýzy při použití úplné informační maximální věrohodnosti na stejném souboru dat poskytnou při každém provedení analýzy stejné výsledky, a výsledky tedy nezávisí na semínku náhodných čísel. Pokud je však hodnota náhodného semínka definována v plánu statistické analýzy, lze tento problém vyřešit.
Omezení použití úplné informační maximální věrohodnosti ve srovnání s vícenásobnou imputací
Omezení použití úplné informační maximální věrohodnosti ve srovnání s použitím vícenásobné imputace spočívá v tom, že použití úplné informační maximální věrohodnosti je možné pouze pomocí speciálně navrženého softwaru . Byl vyvinut navržený předběžný software, ale většina z nich postrádá funkce komerčně navrženého statistického softwaru (například STATA, SAS nebo SPSS). V programech STATA (pomocí příkazu SEM) a SAS (pomocí příkazu PROC CALIS) je možné použít plnou informační maximální věrohodnost, ale pouze při použití spojitých závislých (výsledných) proměnných. Pro logistickou regresi a Coxovu regresi je jediným komerčním balíkem, který poskytuje plnou informační maximální věrohodnost pro chybějící data, Mplus.
Dalším potenciálním omezením při použití plné informační maximální věrohodnosti může být základní předpoklad vícerozměrné normality . Nicméně porušení předpokladu vícerozměrné normality nemusí být tak důležité, takže může být přijatelné zahrnout do analýzy binární nezávislé proměnné .
V doplňkovém souboru 1 jsme zahrnuli program (SAS), který vytváří úplný soubor dat toy včetně několika různých analýz těchto dat. Tabulka 1 a tabulka 2 ukazují výstupy a to, jak různé metody, které zpracovávají chybějící data, dávají různé výsledky.
Regresní analýza hodnot panelu
Panelová data jsou obvykle obsažena v tzv. širokém datovém souboru, kde první řádek obsahuje názvy proměnných a další řádky (jeden pro každého pacienta) obsahují odpovídající hodnoty. Výsledek je reprezentován různými proměnnými – jednou pro každé plánované, časově omezené měření výsledku. Pro analýzu údajů je třeba soubor převést na tzv. dlouhý soubor s jedním záznamem pro každé plánované měření výsledku, který obsahuje hodnotu výsledku, čas měření a kopii všech ostatních hodnot proměnných s výjimkou hodnot proměnné výsledku. Aby se zachovaly korelace v rámci pacienta mezi časovými měřeními výsledku, je běžnou praxí provést vícenásobnou implantaci datového souboru v jeho široké podobě a následnou analýzu výsledného souboru po jeho převedení do dlouhé podoby. Pro analýzu spojitých výsledných hodnot lze použít Proc mixed (SAS 9.4) a pro ostatní typy výsledků Proc glimmix (SAS 9.4). Protože tyto postupy používají přímou metodu maximální věrohodnosti na výsledná data, ale ignorují případy s chybějícími hodnotami kovariát, lze tyto postupy použít přímo, pokud chybí pouze hodnoty závislé proměnné a nejsou k dispozici žádné dobré pomocné proměnné. V opačném případě je třeba po vícenásobném výpočtu použít proc. mixed nebo proc. glimmix (podle toho, co je vhodné). Je zřejmé, že odpovídající přístup může být možný i s použitím jiných statistických balíků.
Analýzy citlivosti
Analýzy citlivosti lze definovat jako soubor analýz, v nichž se s údaji zachází jiným způsobem ve srovnání s primární analýzou. Analýzy citlivosti mohou ukázat, jak předpoklady, odlišné od těch, které byly učiněny v primární analýze, ovlivňují získané výsledky . Analýza citlivosti by měla být předem definována a popsána v plánu statistické analýzy, ale další post hoc analýzy citlivosti mohou být oprávněné a platné. Pokud je potenciální vliv chybějících hodnot nejasný, doporučujeme následující analýzy citlivosti:
-
Již jsme popsali použití analýz citlivosti pro nejlepší a nejhorší případ, abychom ukázali rozsah nejistoty v důsledku chybějících údajů (viz Posouzení, zda by měly být použity metody pro zpracování chybějících údajů). Náš předchozí popis analýz citlivosti pro nejlepší a nejhorší případ se týkal chybějících údajů o dichotomické nebo spojité závislé proměnné, ale tyto analýzy citlivosti lze použít i v případě chybějících údajů o stratifikačních proměnných, výchozích hodnotách atd. Potenciální vliv chybějících údajů by měl být posuzován pro každou proměnnou zvlášť, tj. pro každou proměnnou (závislou proměnnou, ukazatel výsledku a stratifikační proměnné) s chybějícími údaji by měl být jeden nejlepší a jeden nejhorší scénář
-
Pokud je rozhodnuto, že by měly být použity např. vícenásobné imputace, pak by tyto výsledky měly být primárním výsledkem daného výsledku. Každá primární regresní analýza by měla být vždy doplněna odpovídající analýzou pozorovaných (nebo dostupných) případů.
Při použití metod se smíšeným účinkem
Použití designu multicentrické studie bude často nezbytné pro nábor dostatečného počtu účastníků studie v rozumném časovém rámci . Plán multicentrické studie také poskytuje lepší základ pro následné zobecnění jejích výsledků . Bylo prokázáno, že nejčastěji používané metody analýzy v randomizovaných klinických hodnoceních fungují dobře při malém počtu center (analýza binárních závislých výsledků) . Při relativně velkém počtu center (50 a více) je často optimální použít „centrum“ jako náhodný efekt a použít metody analýzy smíšených efektů. Při analýze longitudinálních dat bude často platit i použití metod analýzy smíšených efektů . Za určitých okolností může být platné zahrnout kovariátu „náhodného účinku“ (například „centrum“) jako kovariátu s pevným účinkem během kroku imputace a poté použít analýzu smíšeného modelu nebo zobecněné odhadovací rovnice (GEE) během kroku analýzy . Použití modelu se smíšenými efekty (například s „centrem“ jako náhodným efektem) však znamená, že při modelování vícenásobné imputace je třeba vzít v úvahu vícevrstvou strukturu dat. V současné době není přímo k dispozici komerční software, který by to umožňoval. Lze však použít balíček REALCOME, který lze propojit s programem STATA . Rozhraní exportuje data s chybějícími hodnotami ze STATA do REALCOMu, kde se imputace provádí s ohledem na víceúrovňovou povahu dat a pomocí metody MCMC, která zahrnuje spojité proměnné a pomocí latentního normálního modelu umožňuje také správné zpracování diskrétních dat . Imputované soubory dat lze poté analyzovat pomocí příkazu STATA „mi estimate:“, který lze kombinovat s příkazem „mixed“ (pro spojitý výsledek) nebo příkazem „meqrlogit“ pro binární nebo ordinální výsledek v programu STATA . Při analýze panelových dat se však lze snadno setkat se situací, kdy data zahrnují tři nebo více úrovní, například měření v rámci téhož pacienta (úroveň 1), pacienty v rámci center (úroveň 2) a centra (úroveň 3) . Abychom se nezapletli do poměrně komplikovaného modelu, který může vést k nedostatečné konvergenci nebo nestabilním standardním chybám a pro který není k dispozici komerční software, doporučili bychom buď považovat efekt centra za fixní (přímo nebo po sloučení malých center do jednoho nebo více přiměřeně velkých center pomocí postupu, který musí být předepsán v plánu statistické analýzy), nebo centrum vyloučit jako kovariátu. Pokud byla randomizace rozvrstvena podle center, povede druhý přístup ke zkreslení standardních chyb směrem nahoru, což bude mít za následek poněkud konzervativní testovací postup .
.