Algoritmus Toom-Cook
Zde se dozvíme důmyslnou aplikaci algoritmu rozděl a panuj v kombinaci s lineární algebrou pro rychlé násobení velkých čísel. A také úvod do notace big-O!
Ve skutečnosti je tento výsledek tak protiintuitivní, že se velký matematik Kolmogorov domníval, že takto rychlý algoritmus neexistuje.
Část 0: Dlouhé násobení je pomalé násobení. (A úvod do zápisu Big-O)
Všichni si pamatujeme, jak jsme se ve škole učili násobit. Vlastně se musím k něčemu přiznat. Nezapomeňte, že tohle je zóna bez odsudků 😉
Ve škole jsme měli „mokré hry“, když pršelo příliš silně na to, abychom si mohli hrát na hřišti. Zatímco ostatní (normální/zábavu milující/pozitivní přídavné jméno na výběr) děti hrály hry a blbly, já jsem občas vzal list papíru a násobil velká čísla dohromady, jen tak pro radost. Čirá radost z počítání! Měli jsme dokonce soutěž v násobení, „Super 144“, kde jsme museli co nejrychleji vynásobit zakódovanou mřížku 12 na 12 čísel (od 1 do 12). Cvičil jsem to nábožně do té míry, že jsem měl vlastní předem připravené cvičné listy, které jsem si okopíroval a pak je střídavě používal. Nakonec jsem se dostal na čas 2 minuty a 1 sekundu, při kterém bylo dosaženo mého fyzického limitu čmárání.
Přes tuto posedlost násobením mě nikdy nenapadlo, že bychom to mohli dělat lépe. Strávil jsem násobením tolik hodin, ale nikdy jsem se nepokusil algoritmus vylepšit.
Považte, že násobíme 103 číslem 222.
Vypočítáme 2krát 3krát 1 +2krát 0krát 10 + 2krát 1krát 100 + 20krát 3krát 1 + 20krát 0krát 10 + 20krát 1krát 100 = 22800
Všeobecně platí, že k násobení n-ciferných čísel je třeba O(n²) operací. Zápis „velké O“ znamená, že kdybychom chtěli vykreslit graf počtu operací jako funkci n, záleží skutečně na členu n². Tvar je v podstatě kvadratický.
Dnes si splníme všechny své dětské sny a tento algoritmus vylepšíme. Ale nejdříve! Čeká nás Big-O.
Big-O
Podívejte se na dva grafy níže

Ptejte se matematika „je x² a x²+x^(1/3) totéž?“ a pravděpodobně se pozvrací do šálku kávy, začne brečet a mumlat něco o topologii. Alespoň taková byla moje reakce (zpočátku), a to o topologii sotva něco vím.
Ok. To není totéž. Ale náš počítač se o topologii nezajímá. Počítače se liší ve výkonu tolika způsoby, že to ani nedokážu popsat, protože o počítačích nic nevím.
Ale nemá smysl ladit parní válec. Pokud dvě funkce pro velké hodnoty svých vstupů rostou řádově stejně, pak to pro praktické účely obsahuje většinu relevantních informací.
V grafu výše vidíme, že obě funkce vypadají pro velké vstupy dost podobně. Stejně tak jsou si ale podobné i funkce x² a 2x² – ta druhá je pouze dvakrát větší než ta první. Při x = 100 je jedna z nich 10 000 a druhá 20 000 bodů. To znamená, že pokud dokážeme vypočítat jednu, pravděpodobně dokážeme vypočítat i druhou. Zatímco funkce, která roste exponenciálně, řekněme 10^x, je při x = 100 již mnohem větší než počet atomů ve vesmíru. (10¹⁰⁰ >>>> 10⁸⁰, což je podle mého googlování* odhad, Eddingtonovo číslo, počtu atomů ve vesmíru).
*ve skutečnosti jsem použil DuckDuckGo.
Zapsat celá čísla jako polynomy je velmi přirozené a zároveň velmi nepřirozené. Zápis 1342 = 1000 + 300 + 40 + 2 je velmi přirozený. Zápis 1342 = x³+3x²+4x + 2, kde x = 10, je poněkud zvláštní.
Všeobecně předpokládejme, že chceme vynásobit dvě velká čísla zapsaná v základu b, z nichž každé má n číslic. Každé n-ciferné číslo zapíšeme jako polynom. Rozdělíme-li n-ciferné číslo na r částí, má tento polynom n/r členů.
Například nechť b = 10, r = 3 a naše číslo je 142,122,912
Můžeme to převést na
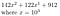
To funguje velmi pěkně, když r = 3 a naše číslo zapsané v základu 10 mělo 9 číslic. Pokud r nedělí n dokonale, můžeme prostě přidat několik nul na začátek. Opět to nejlépe ilustruje příklad:
27134 = 27134 + 0*10⁵ = 027134, což si představíme jako
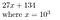
Proč by to mohlo být užitečné? Pro nalezení koeficientů polynomu P platí, že pokud je polynom řádu N, pak jeho vzorkováním v N+1 bodech můžeme určit jeho koeficienty.
Například pokud polynom x⁵ + 3x³ +4x-2, který je řádu 5, vzorkujeme v 6 bodech, můžeme pak celý polynom vypočítat.
Intuitivně má polynom řádu 5 6 koeficientů: koeficient 1, x, x², x³, x⁴, x⁵. Máme-li k dispozici 6 hodnot a 6 neznámých, můžeme tyto hodnoty zjistit.
(Pokud znáte lineární algebru, můžete různé mocniny x považovat za lineárně nezávislé vektory, vytvořit matici pro vyjádření informace, invertovat matici a voila)
Vzorkování polynomů pro určení koeficientů (nepovinné)
Podíváme se trochu hlouběji na logiku vzorkování polynomu pro odvození jeho koeficientů. Klidně přejděte na další část.
Ukážeme si, že pokud se dva polynomy stupně N shodují v N+1 bodech, pak musí být stejné. Tzn. že N+1 bodů jednoznačně určuje polynom stupně N.
Uvažujme polynom stupně 2.
Podívejme se na polynom stupně 2. Ten má tvar P(z) = az² +bz + c. Podle základní věty algebry – nestydatá vsuvka zde, strávil jsem několik měsíců sestavováním důkazu a jeho následným sepsáním, zde – lze tento polynom faktorizovat. To znamená, že ho můžeme zapsat jako A(z-r)(z-w)
Všimněte si, že při z = r a při z = w má polynom hodnotu 0. Říkáme, že w a r jsou kořeny polynomu.
Nyní ukážeme, že P(z) nemůže mít více než dva kořeny. Předpokládejme, že má tři kořeny, které nazveme w, r, s. Pak polynom faktorizujeme. P(z) = A(z-r)(z-w). Pak P(s) = A(s-r)(s-w). To se nerovná 0, protože násobením nenulových čísel získáme nenulové číslo. To je rozpor, protože náš původní předpoklad byl, že s je kořenem polynomu P.
Tento argument lze aplikovat na polynom řádu N v podstatě identickým způsobem.
Předpokládejme nyní, že dva polynomy P a Q řádu N se shodují v N+1 bodech. Pak, pokud se liší, je P-Q polynom řádu N, který je v N+1 bodech roven nule. Podle předchozího to není možné, protože polynom řádu N má nejvýše N kořenů. Náš předpoklad tedy musel být chybný, a pokud se P a Q shodují v N+1 bodech, jde o tentýž polynom.
Vidět znamená věřit: V základu 10 má p 24 číslic (n=24) a rozdělíme ho na 4 části (r=4). n/r = 24/4 = 6
p = 292,103,243,859,143,157,364,152.
A polynom, který jej reprezentuje, nazvěme P,
P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152
s P(10⁶) = p.
Jelikož stupeň tohoto polynomu je 3, můžeme z výběru na 4 místech vypočítat všechny koeficienty. Udělejme si představu o tom, co se stane, když jej budeme vzorkovat na několika místech.
- P(0) = 364,152
- P(1) = 1,043,271
- P(-1) = 172,751
- P(2) = 3,962,726
Zarážející je, že všechny mají 6 nebo 7 číslic. To je ve srovnání s 24 číslicemi, které se původně nacházely v p.
Násobme p číslem q. Nechť q = 124,153,913,241,143,634,899,130 a
Q(x) = 124,153 x³ + 913,241 x²+143,634 x + 899,130
Výpočet t=pq by mohl být hrozný. Ale místo toho, abychom to udělali přímo, zkusíme spočítat polynomickou reprezentaci t, kterou označíme T. Protože P je polynom řádu r-1=3 a Q je polynom řádu r-1 = 3, T je polynom řádu 2r-2=6.
T(10⁶) = t = pq
T(10⁶) = P(10⁶)Q(10⁶)
Vtip je v tom, že koeficienty T nebudeme přímo násobit p a q, ale budeme je vypočítávat. Pak je výpočet T(1⁰⁶) snadný, protože k násobení 1⁰⁶ stačí přilepit 6 nul. Sečíst všechny části je také snadné, protože sčítání je pro počítače velmi levný úkon.
Pro výpočet koeficientů T ho musíme vzorkovat ve 2r-1 = 7 bodech, protože je to polynom 6. řádu. Pravděpodobně budeme chtít vybírat malá celá čísla, takže zvolíme
- T(0)=P(0)Q(0)= 364 152*899 130
- T(1)=P(1)Q(1)= 1 043 271*2 080 158
- T(2)=P(2)Q(2)= 3 962 726*5 832 ,586
- T(-1)=P(-1)Q(-1)= 172751*1544584
- T(-2)=P(-2)Q(-2)= -1,283,550*3,271,602
- T(3)=P(-3)Q(-3)= -5 757 369*5 335 266
Všimněte si velikosti P(-3), Q(-3), P(2), Q(2) atd…. Všechna tato čísla mají přibližně n/r = 24/4 = 6 číslic. Některá jsou šestimístná, některá sedmimístná. S rostoucím n se tato aproximace stává stále rozumnější.
Zatím jsme problém zredukovali na následující kroky, resp. algoritmus:
(1) Nejprve vypočítáme P(0), Q(0), P(1), Q(1) atd (nízkonákladová akce)
(2) Abychom získali naše 2r-1 = 7 hodnot T(x), musíme nyní vynásobit 2r-1 čísel o přibližné velikosti n/r číslic. Konkrétně musíme vypočítat P(0)Q(0), P(1)Q(1), P(-1)Q(-1) atd. (Akce s vysokými náklady)
(3) Rekonstruujte T(x) z našich datových bodů. (Nízkonákladová akce: ale bude přicházet v úvahu později).
(4) S naším rekonstruovaným T(x) vyhodnoťte T(10⁶) v tomto případě
To pěkně vede k analýze doby běhu tohoto přístupu.
Čas běhu
Z výše uvedeného jsme zjistili, že při dočasném zanedbání nízkonákladových akcí (1) a (3) budou náklady na vynásobení dvou n-ciferných čísel Toomovým algoritmem odpovídat:
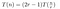
To jsme viděli v řešeném příkladu. Vynásobit každé P(0)Q(0), P(1)Q(1) atd. stojí T(n/r), protože násobíme dvě čísla délky přibližně n/r. Musíme to udělat 2r-1krát, protože chceme vzorkovat T(x) – jakožto polynom řádu 2r-2 – na 2r-1 místech.
Jak je to rychlé? Takovou rovnici můžeme řešit explicitně.

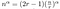
Nyní už zbývá jen nějaké chaotická algebra
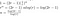
Ještě nějaké další náklady z procesu násobení („skládání“) matic, a ze sčítání, nemůžeme skutečně říci, že naše řešení je přesný čas běhu, takže místo toho dojdeme k závěru, že jsme našli velké O času běhu
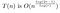
Optimalizace r
Tento čas běhu ještě závisí na r. Opravte r a máme hotovo. Naše zvědavost však ještě není ukojena!!!
Když se n zvětšuje, chceme najít přibližně optimální hodnotu pro naši volbu r. Tj. chceme zvolit hodnotu r, která se mění pro různé hodnoty n.
Klíčové je, že při měnícím se r musíme věnovat pozornost nákladům na opětovné sestavení – matice, která tuto operaci provádí, má náklady O(r²). Když bylo r pevné, nemuseli jsme se tím zabývat, protože s růstem n při pevném r to byly členy zahrnující n, které určovaly růst toho, kolik výpočtu bylo potřeba. Protože naše optimální volba r bude s rostoucím n stále větší, nemůžeme to již ignorovat.
Tento rozdíl je zásadní. Zpočátku naše analýza zvolila hodnotu r, možná 3, možná 3 miliardy, a pak se podívala na velikost velkého O, když n libovolně rostlo. Nyní se díváme na chování, když n roste libovolně velké a r roste s n nějakou námi určenou rychlostí. Tato změna pohledu se dívá na O(r²) jako na proměnnou, zatímco když bylo r pevně dané, bylo O(r²) konstantou, i když jsme ji neznali.
Aktualizujeme tedy naši analýzu z dřívějška:
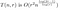
kde O(r²) představuje náklady na sestavení matice. Nyní chceme pro každou hodnotu n zvolit takovou hodnotu r, která tento výraz přibližně minimalizuje. Abychom minimalizovali, zkusíme nejprve diferencovat vzhledem k r. Tím získáme poněkud ohavně vypadající výraz

Normálně, abychom našli minimální bod, nastavíme derivaci rovnou 0. Tento výraz ale nemá pěkné minimum. Místo toho najdeme „dostatečně dobré“ řešení. Jako hostovanou hodnotu použijeme r = r^(sqrt(logN)). Graficky je to docela blízko minima. (V grafu níže je faktor 1/1000 proto, aby byl graf viditelný v rozumném měřítku)
Na grafu níže je naše funkce pro T(N), škálovaná konstantou, vyznačena červeně. Zelená čára je v bodě x = 2^sqrt(logN), což byla naše odhadovaná hodnota. Na místě ‚x‘ je ‚r‘ a na každém ze tří obrázků je použita jiná hodnota N.



To mě docela přesvědčuje, že naše volba byla dobrá. S touto volbou r ji můžeme zapojit a podívat se, jak vypadá konečné big-O našeho algoritmu:

kde jsme jednoduše zapojili naši hodnotu pro r a použili aproximaci pro log(2r-1)/log(r), která je pro velké hodnoty r velmi přesná.
Jak velké je to zlepšení?“
Možná to, že jsem si tohoto algoritmu nevšiml, když jsem jako malý kluk násobil, bylo rozumné. V grafu níže uvádím koeficient naší funkce big-O 10 (pro demonstrační účely) a dělím ho x² (protože původní přístup k násobení byl O(n²). Pokud by červená přímka směřovala k 0, ukázalo by to, že náš nový čas běhu je asymptoticky lepší než O(n²).
A skutečně, i když tvar funkce ukazuje, že náš přístup je nakonec rychlejší, a nakonec je mnohem rychlejší, musíme počkat, až budeme mít téměř 400 místná dlouhá čísla, aby tomu tak bylo! I kdyby byl koeficient jen 5, čísla by musela být dlouhá asi 50 číslic, aby došlo ke zlepšení rychlosti.

Pro mé desetileté já by násobení 400místných čísel bylo trochu náročné! Sledovat různá rekurzivní volání mé funkce by bylo také poněkud skličující. Ale pro počítač řešící úlohu v umělé inteligenci nebo ve fyzice je to běžný problém!“
Jak hluboký je tento výsledek?
Na této technice se mi líbí, že to není žádná raketová věda. Není to ta nejzamotanější matematika, která kdy byla objevena. Při zpětném pohledu se to možná jeví jako samozřejmost!“
Však právě v tom spočívá genialita a krása matematiky. Četl jsem, že Kolmogorov na jednom semináři vyslovil domněnku, že násobení je v podstatě O(n²). Kolmogorov v podstatě vynalezl spoustu moderní teorie pravděpodobnosti a analýzy. Byl jedním z matematických velikánů 20. století. Přesto se ukázalo, že v této nesouvisející oblasti čeká na objevení celý korpus znalostí, který jemu i všem ostatním leží přímo pod nosem!“
Ve skutečnosti se dnes poměrně rychle vybaví algoritmy Rozděl a panuj, protože se běžně používají. Jsou však produktem počítačové revoluce v tom smyslu, že teprve s obrovským výpočetním výkonem se lidské mozky zaměřily právě na rychlost výpočtů jako na oblast matematiky hodnou samostatného studia.
Proto nejsou matematici ochotni přijmout Riemannovu hypotézu za pravdivou jen proto, že se zdá, že by mohla být pravdivá, nebo že P se nerovná NP jen proto, že se to zdá nejpravděpodobnější. Úžasný svět matematiky si vždy zachovává schopnost zmást naše očekávání.
Ve skutečnosti lze najít ještě rychlejší způsoby násobení. Současné nejlepší přístupy používají rychlé Fourierovy transformace. Ale to si nechám na jindy 🙂
Dole mi dejte vědět, co si o tom myslíte. Nově jsem na Twitteru jako ethan_the_mathmo, můžete mě sledovat zde.
Na tento problém jsem narazil v úžasné knize, kterou používám, s názvem „The Nature of Computation“ od fyziků Moora a Mertense, kde vás jeden z problémů provede rozborem Toomova algoritmu.