Jak pomoci žákům, kteří mají problémy se slovními úlohami

„Znají matematiku. Jen neumějí řešit slovní úlohy. Jde o jejich čtení s porozuměním.“

Paní Hartwellová vysvětlovala, proč měli její studenti problémy při státních testech. Své studenty znala a provedla dostatečné hodnocení. Byla si jistá, že jejich potíže jsou problémem čtenářské gramotnosti.

„Nechápu, proč jim to čtení dělají tak těžké. Děti už dělají test z jazyků.“

S paní Hartwellovou (a dalšími žáky její školy) jsem se spojila v rámci newyorského programu na zlepšení výsledků v matematice. Cílem bylo zavést koncepční matematiku do škol „prvního stupně“. Školy úrovně 1 byly ty, které vedly ve městě ve třech oblastech. Nejnižší příjem, nejnižší výsledky v testech a nejvyšší procento barevných žáků.

Vysvětlení o „gramotnosti“ jsem slyšel od jiných učitelů v programu. A dávalo to smysl. Pokud žáci znali matematiku, proč by jinak měli problémy v testu, který obsahoval spoustu slovních úloh?

Ale mělo to háček. Za poslední tři roky se úroveň čtenářské gramotnosti v celém městě zvýšila z 30-40 %. Ve stejném období zůstaly výsledky v matematice většinou stejné.

Pokud by se jednalo o problém se čtením, zvýšení výsledků ve čtení by mělo odblokovat explozivní růst v matematice. Kromě toho se mi jazyk ve slovních úlohách nezdál dost složitý na to, aby mi dělal potíže.

Na příští hodinu jsem měla navštívit třídu slečny Hartwellové. Měla naplánovanou hodinu o slovních úlohách, takže jsem se o problému mohl přesvědčit z první ruky.

Přehled slovních úloh

Žáci seděli u kulatých stolů a ona stála vepředu. Ona i její studenti měli všichni ruční tabule.

Otevřeli učebnice na straně 47 a ona nahlas přečetla slovní úlohu. „Sarah má 40 liber mrkve pro své koně. Pokud má 100 koní, kolik liber dostane každý kůň?“ „Ano,“ odpověděla.

„Dobře, třído, má 40 liber, které dá každému koni. Jakou operaci tedy potřebujeme?“

Ukázala na kotevní tabulku, kde jsou uvedena „klíčová slova“ pro jednotlivé operace. ‚Každá‘ byla na začátku seznamu dělení.“

„Dělení!“ odpověděla třída.“

„Správně. Jak tedy dělíme malé číslo velkým číslem?“

Třída ztichla. Paní Hartwellová nakreslila na tabuli vinkula (domeček pro dlouhé dělení). Studenti kopírovali, jak pod domeček umístila 40 a mimo něj 100.

„Nyní se 100 nevejde do 40, takže musíme přidat desetinné číslo.“ Změnila 40 na 40,0. „Kolikrát se 100 vejde do 400?“ „Ano,“ odpověděla.

Několik studentů zavolalo „Čtyři!“.

„Přesně tak. Nyní musíme do našeho kvocientu vložit i desetinné číslo. Naše konečná odpověď je?“

Třída přečetla z tabule odpověď: „0,4.“

Zadala podobnou úlohu a ukázala na plakát „CUBES“ na zdi. „Nezapomeňte zakroužkovat čísla a zakroužkovat klíčová slova.“

Při práci žáků kroužila kolem. Někteří se ptali, kam mají dát desetinnou čárku. Jiní měli problém se seřazením odčítací části dlouhého dělení. Někteří studenti pracovali ve dvojicích, kdy jeden počítal, zatímco druhý opisoval.

Na konci hodiny měli všichni na papíře správnou odpověď. „Vidíte?“ Paní Hartwellová poznamenala: „Všichni umí počítat.“

Co bylo špatně?

Přestože se jedná o extrémní příklad, mnohé z chyb, kterých se paní Hartwellová dopustila, jsou ve skutečnosti docela běžné.

K přílišné podpoře dochází, když studentům poskytujeme příliš mnoho podpory. I když je běžné, že se pedagogové pyšní tím, že studentům poskytují „tolik podpory, kolik potřebují“, přílišné lešení je něco jiného.

Termín „lešení“ pochází z díla Lva Vygotského. Ten vytvořil termín „zóna proximálního vývoje“. ZPD zahrnuje věci, které jsou těsně mimo dosah žáka. Nedokáže je zvládnout sám, ale s podporou ano. Pomocí „scaffoldingu“ můžeme tyto dovednosti posunout mezi základní dovednosti žáka.

Často se přehlíží, že scaffolding se vztahuje pouze na dovednosti, které se již nacházejí v ZPD žáka. Existuje celá řada dovedností, které jsou v současné době mimo dosah žáka. Když se pokoušíme tyto dovednosti podřídit lešení, naděláme více škody než užitku.

Jedním z problémů nadměrného podřizování lešení je, že si žáci nikdy neosvojí cílené dovednosti. Když žákovi pomůžeme s něčím, co je mimo jeho ZPD, bude naši pomoc vždy potřebovat. Přinejmenším do té doby, než identifikujeme zprostředkující dovednosti, které jsou v jejich ZPD.

Dalším problémem je, že nadměrné šablonování nám dává falešný pocit úspěchu. V tomto případě paní Hartwellová věřila, že její žáci „zvládnou matematiku“ ve slovní úloze. Ve skutečnosti pouze napodobovali její jednání. Nebyl důvod se domnívat, že by podobné řešení dokázali najít sami.

Z procesu řešení problému také odstranila celý proces „formulace“. Mnoho pedagogů považuje porozumění a formulaci za totéž, ale formulace je samostatná matematická kompetence.

A právě to může být chybějící složkou způsobu, jakým v současné době vyučujete slovní úlohy.

Příručky pro výuku a profesní vzdělávání

Složení: Klíč k úspěchu při řešení slovních úloh

Formulování slovních úloh zahrnuje jejich pochopení. Jde však ještě dál. Formulace se podobá spíše překladu než porozumění.

Když žák čte slovní úlohu, musí nejprve převést písmena na zvuky (dekódování). Poté musí pochopit, co jednotlivá slova znamenají (slovní zásoba). Musí pochopit, jak do sebe slova zapadají ve větě (syntax). A nakonec porozumění vychází ze skládání těchto částí dohromady tak, aby dávaly smysl.

Většina žáků 6. třídy by si mohla přečíst problém paní Hartwellové a snadno by pochopila, že Sarah rozdává koním mrkev. Mnohem méně jich však spojí „rozdělování“ mrkví s dělením.

To je část, která spoustě pedagogů podráží nohy. Nám to připadá tak samozřejmé. „Ona doslova rozděluje mrkev. Jak by mohli nevidět, že je to dělení?“.

Prostě to nevidí. Kdyby to viděli, neviděli byste v učebnách matematiky viset tabulky s klíčovými slovy. A všechno se to vrací do doby, kdy jsme poprvé učili operace.

Proč žáci bojují s formulacemi

Mnoho učitelů na mnoha školách učí žáky, že matematika je předmět, který dává smysl. V jiných školách se však matematika vyučuje jako předmět pamatování.

Příkladem „matematiky jako pamatování“ je, když se studenti učí nazpaměť matematická fakta. Algoritmy jsou však také o pamatování. Položte 120 na 47. Podle těchto kroků sčítejte, podle těchto odčítejte a podle těchto násobte.

Studenti mohou tyto kroky opakovat, aniž by rozuměli velikosti čísel nebo dokonce tomu, co operace znamenají.

Když začneme s pojmy (pomocí vizuálních modelů nebo vět o číslech), studenti se naučí, co operace znamenají. Když přejdeme rovnou k algoritmu, žáci si operace představují jako řadu náhodných kroků.

Každý rok si žáci pamatují a opakují. Za domácí úkol absolvují stejný algoritmus třicetkrát. Změníme čísla a postup zůstane stejný. Ale dejte jim slovní úlohu a nyní musí dávat smysl.

Co nám testy říkají o uvažování

Mohli bychom studentům dát 10 úloh s názvem „Slovní úlohy na dělení“, abychom jim to usnadnili. Nebudou si muset úlohy ani přečíst. Stačí, když zjistí (nebo uhodnou), které číslo je dělitelem a které dělitelem.

Ale když studenti sedí u státního testu, není cílem jim ho usnadnit. Cílem je posoudit, co umí sami.

Tvůrci testů jim nechtějí říkat, jakou operaci mají použít. Dokonce dají klíčová slova pro dělení a sčítání do stejné úlohy. „Ve třídě je 20 žáků. Pokud má každé dítě tři dolary, kolik mají dohromady?“.

Když tedy žáci mají problémy se slovními úlohami, nejde jen o slovní úlohy. Obvykle to znamená, že matematiku dělají zpaměti. Musíme je naučit, že matematika je o vytváření smyslu.

Studenti potřebují k řešení slovních úloh strategie a proces

Částečným problémem systému, jako je CUBES, je to, že se nazývá strategií, ale ve skutečnosti je to proces.

Proces je řada kroků. Jakmile identifikujete efektivní proces, můžete jej opakovat znovu a znovu, aniž byste o tom příliš přemýšleli. Algoritmy jsou procesem. Stejně jako seřazení „od nejvyššího k nejnižšímu“ při procházce na oběd.

Strategie je něco jiného. Strategie vyžadují hluboké porozumění. A schopnost aplikovat porozumění v nových situacích.

Nemůžeme studenty připravit na každý scénář, se kterým se setkají při řešení slovních úloh. Některé vyžadují, aby kombinovali různé matematické dovednosti, které nikdy předtím nekombinovali. Nebo mohou vyžadovat, aby studenti změnili pořadí kroků, aby přišli na správné řešení.

Přemýšlejte o následujícím:

Máte 5 galonů džusu na školní akci se 100 studenty. Jestliže každý kelímek obsahuje 3 oz, kolik kelímků může vypít každý student? Kolik jich zbude.

Postup řešení problému může studentům pomoci začít řešit tento problém. „Určete, na co se ptáte.“ „Zvažte, jaké informace se podávají.“

Neexistuje však žádný stanovený postup, který bychom je mohli naučit, aby jej skutečně vyřešili. Zde přichází na řadu strategie. Potřebují převádět jednotky. Uvědomit si, že dělíme se zbytky, a ne že dělíme úplně. Měli by také pravděpodobně změnit pořadí operací a rozdělit džus do kelímků před dělením počtem studentů.

Neexistuje žádný „trik“, který by studenty k řešení dostal. Musí pochopit význam operací. Potřebují chápat matematiku jako předmět, který dává smysl. A potřebují opakovaně procvičovat aplikaci strategického myšlení na slovní úlohy.

Polyův postup řešení slovních úloh

George Pólya byl vlivný maďarský matematik a stanfordský profesor, který objevil postup, který lze použít k řešení jakýchkoli úloh. Jeho práce zasáhla nespočet matematiků a pedagogů, z nichž většina jeho jméno nezná.

Ve skutečnosti jsou CUBES a další tzv. strategie řešení problémů volně založeny na jeho práci. Problém je v tom, že se ji snaží zjednodušit. Přitom odstraňují vše, co připomíná hluboké myšlení.

Polya věřil, že každý problém lze vyřešit ve čtyřech krocích: Pochopit, naplánovat, vyřešit a promyslet. Myslím, že původní Polyaův čtyřkrokový proces je pro použití ve školách naprosto vyhovující.

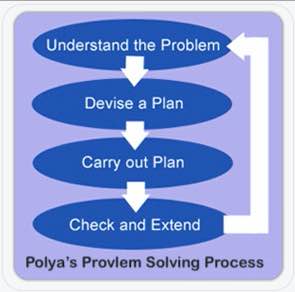Chceme-li problém pochopit, určíme, jaké informace jsou dány a co chceme zjistit. Odtud pocházejí „C“ a „U“ v kostkách. Pokud studenti chtějí zakroužkovat čísla a podtrhnout otázku, dobře. Já dávám přednost tomu, aby si je (s jednotkami) zapsali do grafického organizéru, alespoň zpočátku. Pomáhá jim to zpracovat to, co čtou. Mně jako učiteli to také pomáhá posoudit jejich porozumění, když chodím po místnosti.

Další část je záludná. V „plánu“ formulujeme problém. Vezmeme scénář z reálného světa a převedeme ho do jiné matematické reprezentace.

Třetím krokem je řešení. Pokud jsme správně formulovali, je to místo, kde počítáme. Studenti obvykle používají algoritmus, ale doporučuji používat i rovnice a vizuální modely.

Nakonec se studenti ohlédnou a zkontrolují svou práci. Měli by se také zamyslet nad svým postupem. Pokud jsem udělal chybu, proč? Mohla by mi tato strategie pomoci při řešení podobných úloh v budoucnu?“

Strategie řešení slovních úloh

Mít postup, jak přistupovat ke slovním úlohám, je určitě užitečné. Nemůžeme však předstírat, že smysluplnou matematiku se naučíme jen tím, že budeme postupovat podle jednotlivých kroků. Smyslem slovních úloh je rozšířit matematiku nad rámec „matematických faktů“ a algoritmů.

Existuje několik užitečných strategií, které žákům pomohou s formulací. Zpočátku explicitně učím řadu různých strategií.

Při výuce strategií nechávám studenty řešit problémy, které se k dané strategii hodí. Některé typy problémů se opravdu dobře hodí ke strategii „Hádej a zkontroluj“. K jiným se více hodí ‚Nakresli obrázek‘.

Nakonec jim zadávám náročné slovní úlohy, které lze řešit několika způsoby. Jakmile mají v opasku nástroje, mohou si vybrat, který je pro danou situaci nejlepší.

Kombinace strategií může být také velmi účinná. Například nakreslení obrázku může často pomoci při formulaci. Pokud má farmář 18 řádků mrkve a v každém řádku 10 mrkví, může student začít tím, že nakreslí pole. V určitém okamžiku si může pomyslet: „Páni, to je pole,“ a uvědomí si, že může násobit pomocí mentální matematiky, výrazu nebo algoritmu.

Jindy mohou studenti k formulaci a řešení problému použít vizuální modely.

Pomozte žákům zvládnout náročné slovní úlohy

Jestliže jste jako mnozí učitelé, možná máte obavy, jak to všechno vaši žáci zvládnou. Postupy, strategie, kritické myšlení… je toho hodně.

Možná si dokonce říkáte, že před tímto článkem se vám slovní úlohy zdály jednodušší. Pokud ano, omlouvám se.

Klíčem k úspěchu je nenechat se zahltit snahou zvládnout vše najednou. Začněte řešením jednoduché slovní úlohy pomocí Polyaova postupu. Pak každý týden zavádějte novou strategii. Na konci roku budete překvapeni, jak daleko se dostali.

Možná máte zájem jít hlouběji do kreativního řešení problémů. Zvažte účast na praktickém matematickém semináři nebo spolupráci s online koučem.

Jestliže jste připraveni vnést do své třídy Polya zítra, tento grafický organizér je skvělým způsobem, jak začít. Poslouží jako lešení pro čtyřkrokový proces a pomůže vám určit, kde vaši žáci vybočují z cesty.

Svobodný organizér slovních úloh

O autorovi

Jeff Lisciandrello je zakladatelem společnosti Room to Discover a poradcem v oblasti vzdělávání, který se specializuje na výuku zaměřenou na studenty. Jeho projekt 3-Bridges Design for Learning pomáhá školám zkoumat inovativní postupy v rámci tradičního prostředí. Rád pomáhá pedagogům zavádět badatelské a personalizované přístupy k výuce. Spojit se s ním můžete prostřednictvím Twitteru @EdTechJeff

.