Úvod do podnikové statistiky

Považujte následující soubor dat.
4; 5; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 10

Tento soubor dat lze znázornit následujícím histogramem. Každý interval má šířku jedna a každá hodnota se nachází uprostřed intervalu.

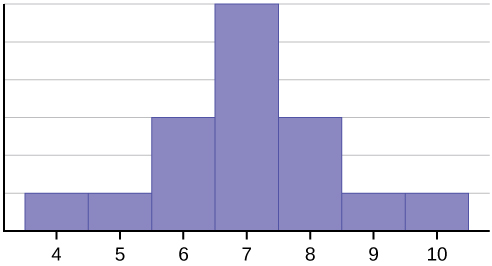
Histogram zobrazuje symetrické rozložení dat. Rozdělení je symetrické, pokud lze v některém bodě histogramu nakreslit svislou čáru tak, že tvar nalevo a napravo od svislé čáry jsou navzájem zrcadlovými obrazy. Střední hodnota, medián a modus jsou pro tato data každý sedm. V dokonale symetrickém rozdělení jsou střední hodnota a medián stejné. Tento příklad má jeden modus (unimodální) a modus je stejný jako průměr a medián. V symetrickém rozdělení, které má dva mody (bimodální), by se oba mody lišily od průměru a mediánu.

Histogram pro tato data: 4566677778 není symetrický. Pravá strana se zdá být „useknutá“ ve srovnání s levou stranou. Rozdělení tohoto typu se nazývá zkosené doleva, protože je vytažené doleva. Šikmost rozdělení můžeme formálně měřit stejně jako můžeme matematicky měřit střední váhu dat nebo jejich obecnou „speadness“. Matematický vzorec pro šikmost je následující: . Čím větší je odchylka od nuly, tím větší je stupeň šikmosti. Pokud je šikmost záporná, pak je rozdělení zkosené doleva jako na (obrázku). Kladná míra šikmosti značí pravé zkosení, jako například (obrázek).

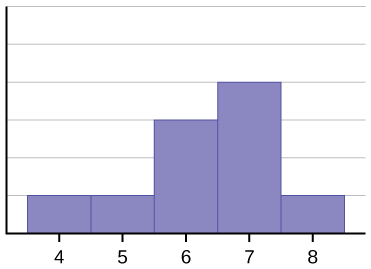
Průměr je 6,3, medián je 6,5 a modus je sedm. Všimněte si, že průměr je menší než medián a oba jsou menší než modus. Průměr i medián odrážejí zkreslení, ale průměr ho odráží více.

Histogram pro data: 67777888910, také není symetrický. Je zkosený doprava.

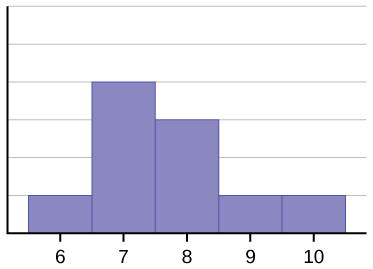
Průměr je 7,7, medián je 7,5 a modus je sedm. Z těchto tří statistik je průměr největší, zatímco modus je nejmenší. Opět platí, že průměr nejvíce odráží zkreslení.

Shrneme-li to, obecně platí, že pokud je rozdělení dat zkreslené doleva, je průměr menší než medián, který je často menší než modus. Je-li rozdělení dat zkosené doprava, je modus často menší než medián, který je menší než průměr.

Stejně jako u průměru, mediánu a modu, a jak brzy uvidíme, i u rozptylu, existují matematické vzorce, které nám poskytují přesné míry těchto vlastností rozdělení dat. Při opětovném pohledu na vzorec pro šikmost vidíme, že se jedná o vztah mezi průměrem dat a jednotlivými pozorováními vynásobenými kubickou hodnotou.

kde je výběrová směrodatná odchylka dat, , je aritmetický průměr a je velikost vzorku.

Formálně je aritmetický průměr znám jako první moment rozdělení. Druhým momentem, který uvidíme, je rozptyl a třetím momentem je šikmost. Rozptyl měří kvadratické rozdíly dat od průměru a šikmost měří kubické rozdíly dat od průměru. Zatímco rozptyl nemůže být nikdy záporné číslo, míra šikmosti může a právě podle ní určíme, zda jsou data zkreslená doprava nebo doleva. Pro normální rozdělení je šikmost rovna nule a jakákoli symetrická data by měla mít šikmost blízkou nule. Záporné hodnoty šikmosti označují data, která jsou vychýlená doleva, a kladné hodnoty šikmosti označují data, která jsou vychýlená doprava. Šikmostí vlevo se rozumí, že levý chvost je delší než pravý chvost. Podobně zkosená doprava znamená, že pravý chvost je dlouhý vzhledem k levému chvostu. Šikmost charakterizuje stupeň asymetrie rozdělení kolem jeho průměru. Zatímco průměr a směrodatná odchylka jsou rozměrové veličiny (proto budeme brát druhou odmocninu z rozptylu ), tj. mají stejné jednotky jako měřené veličiny , šikmost je konvenčně definována tak, aby byla nerozměrová. Je to čisté číslo, které charakterizuje pouze tvar rozdělení. Kladná hodnota šikmosti značí rozdělení s asymetrickým chvostem, který se rozšiřuje směrem ke kladnějšímu X, a záporná hodnota značí rozdělení, jehož chvost se rozšiřuje směrem k zápornějšímu X. Nulová míra šikmosti bude znamenat symetrické rozdělení.

Šikmost a symetrie se stanou důležitými, až budeme v dalších kapitolách probírat rozdělení pravděpodobnosti.