Wie man Schülern hilft, die sich mit Wortproblemen schwer tun

„Sie kennen die Mathematik. Sie können nur die Textaufgaben nicht lösen. Es geht um ihr Leseverständnis.“

Frau Hartwell erklärte, warum ihre Schüler bei den staatlichen Tests so schlecht abgeschnitten hatten. Sie kannte ihre Schüler und hatte sie ausgiebig untersucht. Sie war sich sicher, dass ihre Schwierigkeiten mit der Lesekompetenz zusammenhingen.

„Ich verstehe nicht, warum sie das Lesen so schwer machen. Die Kinder machen doch schon einen Sprachtest.“

Ich wurde mit Frau Hartwell (und anderen an ihrer Schule) im Rahmen eines Programms der Stadt New York zusammengebracht, das die Mathematikleistungen verbessern sollte. Ziel war es, konzeptionelle Mathematik in „Tier 1″-Schulen einzuführen. Tier 1“-Schulen waren diejenigen, die in der Stadt in drei Bereichen führend waren. Geringes Einkommen, niedrigste Testergebnisse und der höchste Anteil farbiger Schüler.

Ich hatte die Erklärung zur „Alphabetisierung“ von anderen Lehrern des Programms gehört. Und es machte Sinn. Wenn die Schüler die Mathematik beherrschten, warum hatten sie dann Probleme bei dem Test, der viele Wortaufgaben enthielt?

Aber es gab einen Haken. In den letzten drei Jahren waren die Lese- und Schreibfähigkeiten stadtweit von 30 % auf 40 % gestiegen. Im gleichen Zeitraum waren die Ergebnisse in Mathematik weitgehend gleich geblieben.

Wenn es sich um ein Leseproblem handeln würde, müssten die Steigerungen bei den Leseleistungen ein explosionsartiges Wachstum in Mathematik auslösen. Außerdem schien die Sprache in den Wortproblemen nicht kompliziert genug zu sein, um Probleme zu verursachen.

In der nächsten Stunde sollte ich die Klasse von Frau Hartwell besuchen. Sie hatte eine Lektion über Wortprobleme geplant, so dass ich das Problem aus erster Hand sehen konnte.

Over-Scaffolding Word Problems

Die Schüler saßen an runden Tischen, und sie stand vorne. Sie und ihre Schüler hatten alle ein Whiteboard in der Hand.

Sie schlugen ihre Lehrbücher auf Seite 47 auf, und sie las ein Wortproblem laut vor. „Sarah hat 40 Pfund Karotten für ihre Pferde. Wenn sie 100 Pferde hat, wie viel Pfund bekommt dann jedes Pferd?“

„OK Klasse, sie hat 40 Pfund, die sie jedem Pferd geben wird. Welche Operation brauchen wir also?“

Sie zeigte auf ein Ankerdiagramm, auf dem die ‚Schlüsselwörter‘ für jede Operation aufgelistet waren. ‚Jede‘ stand ganz oben auf der Liste der Divisionen.

„Division!“, antwortete die Klasse.

„Richtig. Wie teilt man also eine kleine Zahl durch eine große Zahl?“

Die Klasse war still. Frau Hartwell zeichnete ein Vinculum (Haus der langen Teilung) an die Tafel. Die Schüler kopierten es, während sie 40 unter das Haus und 100 nach außen stellte.

„Jetzt passt 100 nicht mehr in 40, also müssen wir eine Dezimalzahl hinzufügen.“ Sie änderte 40 in 40,0. „Wie viele Male passt 100 in 400?“

Ein paar Schüler riefen „Vier!“

„Genau. Jetzt müssen wir auch noch eine Dezimalstelle in unseren Quotienten einsetzen. Unsere endgültige Antwort lautet?“

Die Klasse las die Antwort, „0,4“, von der Tafel ab.

Sie gab eine ähnliche Aufgabe und zeigte auf das „CUBES“-Poster an der Wand. „Denkt daran, die Zahlen einzukreisen und die Schlüsselwörter zu kreuzen.“

Sie ging im Kreis herum, während die Schüler arbeiteten. Einige fragten, wo sie das Komma setzen sollten. Andere hatten Schwierigkeiten, den Subtraktionsteil der langen Division aufzustellen. Einige Schüler arbeiteten zu zweit, wobei einer rechnete, während der andere abschrieb.

Am Ende der Stunde hatte jeder die richtige Antwort auf seinem Papier. „Sehen Sie?“

Was ist falsch gelaufen?

Auch wenn dies ein extremes Beispiel ist, sind viele der Fehler, die Frau Hartwell gemacht hat, ziemlich häufig.

Übermäßiges Scaffolding tritt auf, wenn wir den Schülern zu viel Unterstützung geben. Auch wenn Pädagogen oft stolz darauf sind, den Schülern so viel Unterstützung zu geben, wie sie brauchen, ist eine Überförderung etwas anderes.

Der Begriff „Scaffolding“ stammt aus der Arbeit von Lew Vygotski. Er prägte den Begriff „Zone of Proximal Development“. Die ZPD umfasst Dinge, die gerade außerhalb der Reichweite des Lernenden liegen. Sie können es nicht ganz alleine schaffen, aber mit Unterstützung können sie es schaffen. Durch „Gerüstbau“ können wir diese Fähigkeiten in die Kernfähigkeiten eines Lernenden verschieben.

Was oft übersehen wird, ist, dass Gerüstbau nur für Fähigkeiten gilt, die sich bereits in der ZPD eines Lernenden befinden. Es gibt eine ganze Reihe von Fähigkeiten, die derzeit außerhalb der Reichweite eines Lernenden liegen. Wenn wir versuchen, diese Fähigkeiten zu fördern, schaden wir mehr, als dass wir ihnen nützen.

Ein Problem bei der Überförderung ist, dass die Schüler die angestrebten Fähigkeiten nie verinnerlichen. Wenn wir einem Schüler bei etwas helfen, das außerhalb seines ZPD liegt, wird er immer unsere Hilfe brauchen. Zumindest so lange, bis wir die Zwischenfähigkeiten identifizieren, die in ihrem ZPD liegen.

Ein weiteres Problem ist, dass wir durch übermäßiges Scaffolding ein falsches Gefühl des Erfolgs bekommen. In diesem Fall glaubte Frau Hartwell, dass ihre Schüler das Wortproblem „rechnen“ könnten. In Wirklichkeit ahmten sie aber nur ihre Handlungen nach. Es gab keinen Grund zu der Annahme, dass sie selbst eine ähnliche Lösung finden könnten.

Sie entfernte auch den gesamten Prozess der „Formulierung“ aus dem Problemlösungsprozess. Viele Pädagogen halten Verstehen und Formulieren für ein und dasselbe, aber Formulieren ist eine separate mathematische Kompetenz.

Und das ist vielleicht die fehlende Zutat in der Art und Weise, wie Sie derzeit Wortprobleme unterrichten.

Ressourcen für den Unterricht und professionelles Lernen

Formulierung: Der Schlüssel zum Erfolg bei Wortproblemen

Zum Formulieren von Wortproblemen gehört, sie zu verstehen. Aber es geht darüber hinaus. Die Formulierung ist eher eine Übersetzung als ein Verstehen.

Wenn ein Schüler ein Wortproblem liest, muss er zunächst Buchstaben in Laute umwandeln (Dekodierung). Dann müssen sie verstehen, was die Wörter bedeuten (Vokabular). Sie müssen verstehen, wie die Wörter in einem Satz zusammenpassen (Syntax). Schließlich ergibt sich das Verstehen aus dem Zusammensetzen dieser Teile zu einer Bedeutung.

Die meisten Schüler der 6. Klasse können Frau Hartwells Aufgabe lesen und verstehen, dass Sarah Karotten an ihre Pferde verteilt. Aber weit weniger werden das „Teilen“ der Karotten mit der Division in Verbindung bringen.

Dies ist der Teil, über den viele Pädagogen stolpern. Für uns scheint es so offensichtlich zu sein. „Sie teilt buchstäblich die Karotten auf. Wie können sie nicht sehen, dass es eine Teilung ist.“

Sie sehen es einfach nicht. Wenn sie es täten, würde man keine Schlüsselworttafeln im Matheunterricht hängen sehen. Und das geht auf die Zeit zurück, als wir zum ersten Mal Operationen unterrichteten.

Warum Schüler sich mit dem Formulieren schwer tun

Viele Lehrer in vielen Schulen bringen den Schülern bei, dass Mathematik ein Fach ist, in dem man Sinn macht. Aber in anderen Schulen wird Mathe als Fach des Erinnerns unterrichtet.

Ein Beispiel für „Mathe als Erinnerungsfach“ ist das Auswendiglernen von mathematischen Fakten. Aber bei Algorithmen geht es auch um das Erinnern. Lege 120 auf 47. Befolge diese Schritte, um zu addieren, diese, um zu subtrahieren, und diese, um zu multiplizieren.

Schüler können diese Schritte wiederholen, ohne zu verstehen, wie groß die Zahlen sind oder was die Operationen bedeuten.

Wenn wir mit Konzepten beginnen (indem wir visuelle Modelle oder Zahlensätze verwenden), lernen die Schüler, was die Operationen bedeuten. Wenn wir direkt zu einem Algorithmus übergehen, betrachten die Schüler die Operationen als eine Reihe von zufälligen Schritten.

Jahr für Jahr lassen wir die Schüler sich erinnern und wiederholen. Sie führen denselben Algorithmus 30 Mal als Hausaufgabe durch. Ändern Sie die Zahlen, und der Prozess bleibt derselbe. Aber geben Sie ihnen ein Wortproblem, und jetzt müssen sie es verstehen.

Was uns die Tests über das logische Denken sagen

Wir könnten unseren Schülern 10 Probleme mit dem Titel „Division Word Problems“ geben, um es ihnen leichter zu machen. Sie brauchen die Aufgaben nicht einmal zu lesen. Sie müssen nur herausfinden (oder erraten), welche Zahl der Divisor und welche der Dividend ist.

Aber wenn die Schülerinnen und Schüler eine staatliche Prüfung ablegen, geht es nicht darum, es ihnen leichter zu machen. Das Ziel ist es, zu beurteilen, was sie selbständig tun können.

Die Testautoren wollen ihnen nicht vorschreiben, welche Operation sie verwenden sollen. Sie setzen sogar Schlüsselwörter für Division und Addition in dieselbe Aufgabe. „Es sind 20 Schüler in der Klasse. Wenn jedes Kind drei Dollar hat, wie viel haben sie dann insgesamt?“

Wenn Schüler mit Wortproblemen zu kämpfen haben, geht es also nicht nur um die Wortprobleme. Es bedeutet in der Regel, dass sie Mathe auswendig lernen. Wir müssen ihnen beibringen, dass es in der Mathematik darum geht, einen Sinn zu finden.

Schüler brauchen Strategien und Prozesse, um Wortprobleme zu lösen

Teil des Problems mit einem System wie CUBES ist, dass es sich selbst als Strategie bezeichnet, aber eigentlich ein Prozess ist.

Ein Prozess ist eine Reihe von Schritten. Wenn man einmal einen effizienten Prozess gefunden hat, kann man ihn immer wieder wiederholen, ohne zu viel darüber nachzudenken. Algorithmen sind ein Prozess. Genauso wie die Aufreihung von „Größter zu Kleinster“ für den Gang zum Mittagessen.

Eine Strategie ist etwas anderes. Strategien erfordern ein tiefes Verständnis. Und die Fähigkeit, dieses Verständnis in neuen Situationen anzuwenden.

Wir können die Schüler nicht auf jedes Szenario vorbereiten, dem sie bei einem Wortproblem begegnen. Einige erfordern, dass sie verschiedene mathematische Fähigkeiten kombinieren, die sie noch nie zuvor kombiniert haben. Oder sie müssen die Reihenfolge der Schritte ändern, um auf die richtige Lösung zu kommen.

Betrachten Sie folgendes:

Sie haben 5 Liter Saft für eine Schulveranstaltung mit 100 Schülern. Wenn jeder Becher 3 Unzen fasst, wie viele Becher kann jeder Schüler trinken? Wie viel wird übrig bleiben?

Ein Problemlösungsprozess kann den Schülern helfen, dieses Problem anzugehen. „Identifiziere, was gefragt wird.“ „Überlegen Sie, welche Informationen gegeben werden.“

Aber es gibt keinen festen Prozess, den wir ihnen beibringen können, um das Problem tatsächlich zu lösen. Das ist der Punkt, an dem die Strategie ins Spiel kommt. Sie müssen Einheiten umrechnen. Sie müssen erkennen, dass wir mit Resten dividieren und nicht vollständig dividieren. Wahrscheinlich sollten sie auch die Operationen neu ordnen und den Saft in Becher aufteilen, bevor sie durch die Anzahl der Schüler dividieren.

Es gibt keinen „Trick“, der die Schüler zum Ziel bringt. Sie müssen die Bedeutung der Operationen verstehen. Sie müssen Mathematik als ein Fach verstehen, in dem es um Sinnstiftung geht. Und sie müssen wiederholt üben, strategisches Denken auf Wortprobleme anzuwenden.

Das Polya-Verfahren zum Lösen von Wortproblemen

George Pólya war ein einflussreicher ungarischer Mathematiker und Stanford-Professor, der ein Verfahren fand, mit dem man jedes Problem lösen kann. Seine Arbeit hat unzählige Mathematiker und Pädagogen berührt, von denen die meisten seinen Namen nicht kennen.

Tatsächlich basieren CUBES und andere so genannte Problemlösestrategien lose auf seiner Arbeit. Das Problem ist, dass sie versuchen, sie zu vereinfachen. Dabei entfernen sie alles, was mit tiefem Denken zu tun hat.

Polya glaubte, dass jedes Problem in vier Schritten gelöst werden kann: Verstehen, Planen, Lösen und Reflektieren. Ich denke, Polyas ursprünglicher Vier-Schritte-Prozess ist genau richtig für den Einsatz in Schulen.

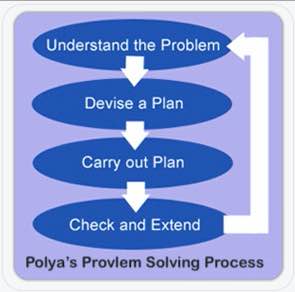Um das Problem zu verstehen, stellen wir fest, welche Informationen gegeben sind und was wir finden wollen. Daher kommen das „C“ und das „U“ in den Würfeln. Wenn die Schüler die Zahlen einkreisen und die Frage unterstreichen wollen, ist das in Ordnung. Ich ziehe es vor, dass sie sie (mit Einheiten) in eine grafische Darstellung schreiben, zumindest am Anfang. Das hilft ihnen, das Gelesene zu verarbeiten. Es hilft auch mir als Lehrer, ihr Verständnis zu beurteilen, während ich durch den Raum gehe.

Nun kommt der schwierige Teil. Im „Plan“ formulieren wir das Problem. Wir nehmen ein Szenario aus der realen Welt und verwandeln es in eine andere mathematische Darstellung.

Der dritte Schritt ist das Lösen. Wenn wir richtig formuliert haben, können wir jetzt rechnen. Die Schüler verwenden in der Regel einen Algorithmus, aber ich ermutige sie auch, Gleichungen und visuelle Modelle zu verwenden.

Zuletzt schauen die Schüler zurück und überprüfen ihre Arbeit. Sie sollten auch über ihren Prozess nachdenken. Wenn ich einen Fehler gemacht habe, warum? Könnte mir diese Strategie helfen, ähnliche Probleme in Zukunft zu lösen?

Strategien zum Lösen von Wortproblemen

Ein Verfahren zum Herangehen an Wortprobleme zu haben, ist definitiv hilfreich. Aber wir können nicht so tun, als würde man sinnvolle Mathematik nur durch das Befolgen von Schritten lernen. Der Sinn von Wortproblemen besteht darin, die Mathematik über „mathematische Fakten“ und Algorithmen hinaus zu erweitern.

Es gibt einige hilfreiche Strategien, um Schülern bei der Formulierung zu helfen. Zunächst lehre ich explizit eine Reihe von verschiedenen Strategien.

Während ich die Strategien unterrichte, lasse ich die Schüler Aufgaben lösen, die gut zu dieser Strategie passen. Einige Problemtypen lassen sich sehr gut mit „Raten und Prüfen“ lösen. Andere eignen sich besser für „Zeichne ein Bild“.

Schließlich gebe ich ihnen anspruchsvolle Wortaufgaben, die auf verschiedene Weise gelöst werden können. Sobald sie die Werkzeuge in ihrem Werkzeuggürtel haben, können sie auswählen, welche für die jeweilige Situation am besten geeignet ist.

Eine Kombination von Strategien kann ebenfalls sehr effektiv sein. Zum Beispiel kann das Zeichnen eines Bildes oft hilfreich sein, um die Formulierung zu erleichtern. Wenn ein Bauer 18 Reihen Karotten hat und in jeder Reihe 10 Karotten stehen, kann ein Schüler damit beginnen, das Feld zu zeichnen. Irgendwann denken sie vielleicht: „Wow, das ist ein Feld“, und erkennen, dass sie mit Hilfe von Kopfrechnen, einem Ausdruck oder einem Algorithmus multiplizieren können.

Andere Male können die Schüler visuelle Modelle verwenden, um das Problem zu formulieren und zu lösen.

Helfen Sie Ihren Schülern bei der Bewältigung schwieriger Wortprobleme

Wenn es Ihnen wie vielen Lehrern geht, machen Sie sich vielleicht Sorgen, wie Ihre Schüler mit all dem umgehen werden. Prozesse, Strategien, kritisches Denken … es geht um viel.

Vielleicht denken Sie sogar, dass Wortprobleme vor diesem Artikel einfacher erschienen. Wenn dem so ist, bitte ich um Entschuldigung.

Der Schlüssel ist, sich nicht zu überwältigen, indem man versucht, alles auf einmal zu tun. Beginnen Sie damit, ein einfaches Wortproblem mit Hilfe des Polya-Verfahrens zu lösen. Führen Sie dann jede Woche eine neue Strategie ein. Am Ende des Jahres werden Sie erstaunt sein, wie weit sie gekommen sind.

Vielleicht möchten Sie das kreative Problemlösen vertiefen. Vielleicht möchten Sie einen praktischen Mathe-Workshop besuchen oder mit einem Online-Coach zusammenarbeiten.

Wenn Sie bereit sind, morgen Polya in Ihr Klassenzimmer zu bringen, ist dieses grafische Organigramm ein guter Anfang. Es unterstützt den vierstufigen Prozess und hilft Ihnen, herauszufinden, wo Ihre Schüler vom Weg abgekommen sind.

Free Word Problem Organizer

Über den Autor

Jeff Lisciandrello ist der Gründer von Room to Discover und ein Bildungsberater, der auf schülerzentriertes Lernen spezialisiert ist. Sein 3-Bridges Design for Learning hilft Schulen dabei, innovative Praktiken in traditionellen Umgebungen zu erforschen. Es macht ihm Spaß, Pädagogen dabei zu helfen, forschungsbasierte und personalisierte Ansätze für den Unterricht zu entwickeln. Sie können mit ihm über Twitter in Kontakt treten @EdTechJeff