Wie man große Zahlen schnell multipliziert

Hier lernen wir eine geniale Anwendung eines Divide-and-Conquer-Algorithmus kombiniert mit linearer Algebra, um große Zahlen schnell zu multiplizieren. Und eine Einführung in die Big-O-Notation!

Dieses Ergebnis ist so kontraintuitiv, dass der große Mathematiker Kolmogorow vermutete, ein so schneller Algorithmus existiere nicht.

Teil 0: Lange Multiplikation ist langsame Multiplikation. (Und eine Einführung in die Big-O-Notation)

Wir alle erinnern uns daran, wie wir in der Schule multiplizieren gelernt haben. Ich muss sogar ein Geständnis ablegen. Denkt daran, dies ist eine urteilsfreie Zone 😉

In der Schule hatten wir „nasse Spiele“, wenn es zu stark regnete, um auf dem Spielplatz zu spielen. Während andere (normale/spaßliebende/positiv-adjektivische) Kinder Spiele spielten und herumalberten, nahm ich manchmal ein Blatt Papier und multiplizierte große Zahlen miteinander, nur so zum Spaß. Die pure Freude am Rechnen! Wir hatten sogar einen Multiplikationswettbewerb, den „Super 144“, bei dem wir ein verschlüsseltes 12-mal-12-Gitter aus Zahlen (von 1 bis 12) so schnell wie möglich multiplizieren mussten. Ich übte das fleißig, und zwar so sehr, dass ich meine eigenen vorbereiteten Übungsblätter hatte, die ich fotokopierte und dann abwechselnd verwendete. Schließlich kam ich auf eine Zeit von 2 Minuten und 1 Sekunde, womit meine physische Grenze beim Kritzeln erreicht war.

Trotz dieser Besessenheit von der Multiplikation kam mir nie in den Sinn, dass wir es besser machen könnten. Ich verbrachte so viele Stunden mit dem Multiplizieren, aber ich versuchte nie, den Algorithmus zu verbessern.

Betrachten wir die Multiplikation von 103 mit 222.

Wir berechnen 2 mal 3 mal 1 + 2 mal 0 mal 10 + 2 mal 1 mal 100 + 20 mal 3 mal 1 + 20 mal 0 mal 10 + 20 mal 1 mal 100 = 22800

Im Allgemeinen benötigt man für die Multiplikation von n-stelligen Zahlen O(n²) Operationen. Die „Big-O“-Notation bedeutet, dass, wenn wir die Anzahl der Operationen als Funktion von n grafisch darstellen würden, der n²-Term wirklich von Bedeutung ist. Die Form ist im Wesentlichen quadratisch.

Heute werden wir alle unsere Kindheitsträume erfüllen und diesen Algorithmus verbessern. Aber zuerst! Big-O wartet auf uns.

Big-O

Sieh dir die beiden Graphen unten an

Fragen Sie einen Mathematiker: „Sind x² und x²+x^(1/3) dasselbe?“, und er wird wahrscheinlich in seine Kaffeetasse kotzen, anfangen zu weinen und etwas über Topologie murmeln. Zumindest war das meine Reaktion (am Anfang), und ich weiß kaum etwas über Topologie.

Ok. Das ist nicht dasselbe. Aber unser Computer kümmert sich nicht um die Topologie. Computer unterscheiden sich in ihrer Leistung auf so viele Arten, dass ich sie nicht einmal beschreiben kann, weil ich nichts über Computer weiß.

Aber es hat keinen Sinn, eine Dampfwalze fein abzustimmen. Wenn zwei Funktionen für große Werte ihrer Eingaben in der gleichen Größenordnung wachsen, dann enthält das für praktische Zwecke die meisten der relevanten Informationen.

In der obigen Grafik sehen wir, dass die beiden Funktionen für große Eingaben ziemlich ähnlich aussehen. Aber auch x² und 2x² sind ähnlich – letztere ist nur doppelt so groß wie die erste. Bei x = 100 ist eine 10.000 und eine 20.000. Das heißt, wenn wir das eine berechnen können, können wir wahrscheinlich auch das andere berechnen. Eine Funktion hingegen, die exponentiell wächst, sagen wir 10^x, ist bei x = 100 bereits weitaus größer als die Anzahl der Atome im Universum. (10¹⁰⁰ >>>> 10⁸⁰, was eine Schätzung, die Eddington-Zahl, für die Anzahl der Atome im Universum ist, wie ich gegoogelt habe*).

*Ich habe DuckDuckGo benutzt.

Ganzzahlen als Polynome zu schreiben ist sowohl sehr natürlich als auch sehr unnatürlich. 1342 = 1000 + 300 + 40 + 2 zu schreiben ist sehr natürlich. 1342 = x³+3x²+4x + 2 zu schreiben, wobei x = 10 ist, ist etwas seltsam.

Angenommen, wir wollen zwei große Zahlen zur Basis b mit jeweils n Ziffern multiplizieren. Wir schreiben jede n-stellige Zahl als ein Polynom. Wenn wir die n-stellige Zahl in r Teile zerlegen, hat dieses Polynom n/r Terme.

Zum Beispiel: b = 10, r = 3, und unsere Zahl ist 142.122.912

Das können wir umwandeln in

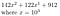
Das funktioniert sehr gut, wenn r = 3 ist und unsere Zahl, geschrieben zur Basis 10, 9 Ziffern hat. Wenn r nicht perfekt durch n teilbar ist, dann können wir einfach ein paar Nullen vorne anhängen. Auch dies lässt sich am besten anhand eines Beispiels veranschaulichen.

27134 = 27134 + 0*10⁵ = 027134, was wir als

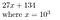
Warum könnte dies hilfreich sein? Um die Koeffizienten des Polynoms P zu finden, kann man, wenn das Polynom die Ordnung N hat, durch Stichproben an N+1 Punkten seine Koeffizienten bestimmen.

Wird zum Beispiel das Polynom x⁵ + 3x³ +4x-2 der Ordnung 5 an 6 Punkten abgetastet, so kann man das gesamte Polynom berechnen.

Intuitiv hat ein Polynom der Ordnung 5 6 Koeffizienten: den Koeffizienten von 1, x, x², x³, x⁴, x⁵. Bei 6 Werten und 6 Unbekannten können wir die Werte herausfinden.

(Wenn du dich mit linearer Algebra auskennst, kannst du die verschiedenen Potenzen von x als linear unabhängige Vektoren behandeln, eine Matrix erstellen, um die Informationen darzustellen, die Matrix invertieren und voila)

Polynome abtasten, um die Koeffizienten zu bestimmen (fakultativ)

Hier sehen wir uns die Logik hinter dem Abtasten eines Polynoms etwas genauer an, um seine Koeffizienten abzuleiten. Sie können gerne zum nächsten Abschnitt übergehen.

Wir werden zeigen, dass zwei Polynome vom Grad N in N+1 Punkten übereinstimmen müssen, wenn sie gleich sind. D.h. N+1 Punkte bestimmen eindeutig ein Polynom der Ordnung N.

Betrachten wir ein Polynom der Ordnung 2. Dieses hat die Form P(z) = az² +bz + c. Nach dem Fundamentalsatz der Algebra – ich habe mehrere Monate damit verbracht, einen Beweis dafür zusammenzustellen und ihn dann hier aufzuschreiben – kann dieses Polynom faktorisiert werden. Das heißt, wir können es als A(z-r)(z-w)

Beachten Sie, dass das Polynom bei z = r und bei z = w den Wert 0 hat. Wir sagen, dass w und r Wurzeln des Polynoms sind.

Nun zeigen wir, dass P(z) nicht mehr als zwei Wurzeln haben kann. Nehmen wir an, es hätte drei Wurzeln, die wir w, r, s nennen. Wir faktorisieren dann das Polynom. P(z) = A(z-r)(z-w). Dann ist P(s) = A(s-r)(s-w). Dies ist nicht gleich 0, da die Multiplikation von Zahlen, die nicht Null sind, eine Zahl ergibt, die nicht Null ist. Das ist ein Widerspruch, denn unsere ursprüngliche Annahme war, dass s eine Wurzel des Polynoms P ist.

Dieses Argument lässt sich auf ein Polynom der Ordnung N auf im Wesentlichen identische Weise anwenden.

Nun nehmen wir an, dass zwei Polynome P und Q der Ordnung N in N+1 Punkten übereinstimmen. Dann ist P-Q, wenn sie verschieden sind, ein Polynom der Ordnung N, das in N+1 Punkten 0 ist. Nach dem Vorhergehenden ist dies unmöglich, da ein Polynom der Ordnung N höchstens N Wurzeln hat. Unsere Annahme muss also falsch gewesen sein, und wenn P und Q in N+1 Punkten übereinstimmen, sind sie dasselbe Polynom.

Sehen ist Glauben: A Worked Example

Betrachten wir eine wirklich große Zahl, die wir p nennen. Zur Basis 10 ist p 24 Stellen lang (n=24), und wir teilen es in 4 Teile auf (r=4). n/r = 24/4 = 6

p = 292,103,243,859,143,157,364,152.

Und das Polynom, das dies repräsentiert, soll P heißen,

P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152

mit P(10⁶) = p.

Da der Grad dieses Polynoms 3 ist, können wir alle Koeffizienten durch Stichproben an 4 Stellen ermitteln. Wir wollen ein Gefühl dafür bekommen, was passiert, wenn wir an einigen Stellen eine Stichprobe machen.

• P(0) = 364.152
• P(1) = 1.043.271
• P(-1) = 172.751
• P(2) = 3.962.726

Auffallend ist, dass diese Zahlen alle 6 oder 7 Stellen haben. Das ist im Vergleich zu den 24 Ziffern, die ursprünglich in p gefunden wurden.

Lassen Sie uns p mit q multiplizieren. Lassen Sie q = 124,153,913,241,143,634,899,130, und

Q(x) = 124,153 x³ + 913,241 x²+143,634 x + 899,130

Die Berechnung von t=pq könnte schrecklich sein. Aber statt es direkt zu tun, versuchen wir, die Polynomdarstellung von t zu berechnen, die wir mit T bezeichnen. Da P ein Polynom der Ordnung r-1=3 ist und Q ein Polynom der Ordnung r-1 = 3 ist, ist T ein Polynom der Ordnung 2r-2 = 6.

T(10⁶) = t = pq

T(10⁶) = P(10⁶)Q(10⁶)

Der Trick ist, dass wir die Koeffizienten von T ausrechnen, anstatt p und q direkt miteinander zu multiplizieren. Dann ist die Berechnung von T(1⁰⁶) einfach, denn um mit 1⁰⁶ zu multiplizieren, kleben wir einfach 6 Nullen auf die Rückseite. Das Zusammenzählen aller Teile ist ebenfalls einfach, da die Addition für Computer sehr kostengünstig ist.

Um die Koeffizienten von T zu berechnen, müssen wir an 2r-1 = 7 Punkten eine Stichprobe machen, da es sich um ein Polynom der Ordnung 6 handelt. Wir wollen wahrscheinlich kleine ganze Zahlen wählen, also wählen wir

• T(0)=P(0)Q(0)= 364,152*899,130
• T(1)=P(1)Q(1)= 1,043,271*2,080,158
• T(2)=P(2)Q(2)= 3,962,726*5,832,586
• T(-1)=P(-1)Q(-1)= 172751*1544584
• T(-2)=P(-2)Q(-2)= -1.283.550*3.271,602
• T(3)=P(-3)Q(-3)= -5.757.369*5.335.266

Beachte die Größe von P(-3), Q(-3), P(2), Q(2) usw… Dies sind alles Zahlen mit ungefähr n/r = 24/4 = 6 Ziffern. Einige sind 6-stellig, andere sind 7-stellig. Je größer n wird, desto vernünftiger wird diese Annäherung.

Bislang haben wir das Problem auf die folgenden Schritte bzw. den folgenden Algorithmus reduziert:

(1) Berechnen Sie zunächst P(0), Q(0), P(1), Q(1) usw. (eine Aktion mit geringem Aufwand)

(2) Um unsere 2r-1= 7 Werte von T(x) zu erhalten, müssen wir nun 2r-1 Zahlen mit der ungefähren Größe von n/r Stellen multiplizieren. Das heißt, wir müssen P(0)Q(0), P(1)Q(1), P(-1)Q(-1) usw. berechnen. (Aktion mit hohen Kosten)

(3) Rekonstruiere T(x) aus unseren Datenpunkten. (Low cost action: wird aber später in Betracht gezogen).

(4) Mit unserem rekonstruierten T(x) bewerten wir T(10⁶) in diesem Fall

Das führt schön zu einer Analyse der Laufzeit dieses Ansatzes.

Laufzeit

Aus dem oben Gesagten haben wir herausgefunden, dass die Kosten für die Multiplikation von zwei n-stelligen Zahlen mit dem Toom-Algorithmus, wenn man die kostengünstigen Aktionen (1) und (3) vorübergehend ignoriert, folgendermaßen aussehen:

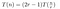
Das haben wir im Arbeitsbeispiel gesehen. Die Multiplikation von P(0)Q(0), P(1)Q(1) usw. kostet T(n/r), weil wir zwei Zahlen der Länge von ungefähr n/r multiplizieren. Wir müssen dies 2r-1 Mal tun, da wir T(x) – das ein Polynom der Ordnung 2r-2 ist – an 2r-1 Stellen abtasten wollen.

Wie schnell ist das? Wir können diese Art von Gleichung explizit lösen.

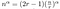
Alles, was jetzt noch bleibt, ist etwas chaotische Algebra

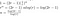
Da es bei der Matrixmultiplikation („Zusammensetzen“) einige andere Kosten gab, und aus der Addition, können wir nicht wirklich sagen, dass unsere Lösung die exakte Laufzeit ist, also schließen wir stattdessen, dass wir das Big-O der Laufzeit gefunden haben

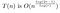
Optimierung von r

Diese Laufzeit hängt noch von r ab. Fix r, und wir sind fertig. Aber unsere Neugier ist noch nicht befriedigt!

Wenn n groß wird, wollen wir einen annähernd optimalen Wert für unsere Wahl von r finden. D.h. wir wollen einen Wert von r wählen, der sich für verschiedene Werte von n ändert.

Das Wichtigste dabei ist, dass wir bei variierendem r die Kosten für die Neuzusammensetzung beachten müssen – die Matrix, die diese Operation durchführt, hat Kosten von O(r²). Als r noch fest war, mussten wir darauf nicht achten, denn als n bei festem r größer wurde, waren es die Terme mit n, die das Wachstum des Rechenaufwands bestimmten. Da unsere optimale Wahl von r größer wird, wenn n größer wird, können wir dies nicht länger ignorieren.

Dieser Unterschied ist entscheidend. Ursprünglich wählte unsere Analyse einen Wert von r, vielleicht 3, vielleicht 3 Milliarden, und betrachtete dann die Big-O-Größe, wenn n beliebig groß wurde. Jetzt betrachten wir das Verhalten, wenn n beliebig groß wird und r mit n mit einer von uns festgelegten Rate wächst. Dieser Perspektivwechsel betrachtet O(r²) als Variable, während O(r²) bei einem festen r eine Konstante war, wenn auch eine, die wir nicht kannten.

So aktualisieren wir unsere Analyse von vorher:

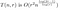
wobei O(r²) die Kosten der Wiederzusammensetzungsmatrix darstellt. Wir wollen nun für jeden Wert von n einen Wert von r wählen, der diesen Ausdruck näherungsweise minimiert. Um zu minimieren, versuchen wir zunächst, nach r zu differenzieren. Dies ergibt den etwas abscheulich aussehenden Ausdruck

Normalerweise setzen wir, um den Minimalpunkt zu finden, die Ableitung gleich 0. Aber dieser Ausdruck hat kein schönes Minimum. Stattdessen finden wir eine Lösung, die „gut genug“ ist. Wir verwenden r = r^(sqrt(logN)) als unseren Schätzwert. Grafisch gesehen ist dies ziemlich nahe am Minimum. (Im folgenden Diagramm dient der Faktor 1/1000 dazu, das Diagramm in einem vernünftigen Maßstab sichtbar zu machen)

Das folgende Diagramm zeigt unsere Funktion für T(N), skaliert mit einer Konstanten, in Rot. Die grüne Linie liegt bei x = 2^sqrt(logN), dem von uns geschätzten Wert. x“ wird durch „r“ ersetzt, und in jedem der drei Bilder wird ein anderer Wert von N verwendet.

Das ist für mich ziemlich überzeugend, dass unsere Wahl eine gute war. Mit dieser Wahl von r können wir es einstecken und sehen, wie das endgültige Big-O unseres Algorithmus aussieht:

wo wir einfach unseren Wert für r einstecken und eine Annäherung für log(2r-1)/log(r) verwenden, die für große Werte von r sehr genau ist.

Wie groß ist die Verbesserung?

Vielleicht war es vernünftig, dass ich diesen Algorithmus nicht entdeckte, als ich als kleiner Junge die Multiplikation beherrschte. Im folgenden Diagramm gebe ich den Koeffizienten unserer Big-O-Funktion mit 10 an (zu Demonstrationszwecken) und teile ihn durch x² (da der ursprüngliche Ansatz für die Multiplikation O(n²) war). Wenn die rote Linie gegen 0 tendiert, würde das zeigen, dass unsere neue Laufzeit asymptotisch besser ist als O(n²).

Und in der Tat, während die Form der Funktion zeigt, dass unser Ansatz schließlich schneller ist, und schließlich ist er viel schneller, müssen wir warten, bis wir fast 400 Stellen lange Zahlen haben, damit dies der Fall ist! Selbst wenn der Koeffizient nur 5 wäre, müssten die Zahlen etwa 50 Stellen lang sein, um eine Geschwindigkeitsverbesserung zu erzielen.

Für mein 10-jähriges Ich wäre die Multiplikation von 400-stelligen Zahlen eine ziemliche Herausforderung! Den Überblick über die verschiedenen rekursiven Aufrufe meiner Funktion zu behalten, wäre auch etwas entmutigend. Aber für einen Computer, der eine Aufgabe in der künstlichen Intelligenz oder in der Physik löst, ist das ein ganz normales Problem!

Wie tiefgreifend ist dieses Ergebnis?

Was ich an dieser Technik so liebe, ist, dass sie keine Raketenwissenschaft ist. Es ist nicht die verblüffendste Mathematik, die je entdeckt wurde. Im Nachhinein erscheint es vielleicht offensichtlich!

Doch das ist die Brillanz und Schönheit der Mathematik. Ich habe gelesen, dass Kolmogorow in einem Seminar vermutet hat, dass die Multiplikation grundsätzlich O(n²) ist. Kolmogorov hat im Grunde genommen einen Großteil der modernen Wahrscheinlichkeitstheorie und Analyse erfunden. Er war einer der großen Mathematiker des 20. Jahrhunderts. Jahrhunderts. Doch als es um dieses nicht verwandte Gebiet ging, stellte sich heraus, dass ein ganzer Wissensfundus darauf wartete, entdeckt zu werden, und zwar direkt vor seiner und aller anderen Nase!

In der Tat kommen einem die Divide-and-Conquer-Algorithmen heute ziemlich schnell in den Sinn, da sie so häufig verwendet werden. Aber sie sind ein Produkt der Computerrevolution, denn erst mit der enormen Rechenleistung hat sich der menschliche Verstand speziell auf die Rechengeschwindigkeit als einen Bereich der Mathematik konzentriert, der eine eigene Untersuchung wert ist.

Deshalb sind Mathematiker nicht bereit, die Riemannsche Hypothese als wahr zu akzeptieren, nur weil es so aussieht, als könnte sie wahr sein, oder dass P nicht gleich NP ist, nur weil das am wahrscheinlichsten erscheint. Die wunderbare Welt der Mathematik ist immer in der Lage, unsere Erwartungen zu übertrumpfen.

In der Tat kann man sogar noch schnellere Wege zum Multiplizieren finden. Die derzeit besten Ansätze verwenden schnelle Fourier-Transformationen. Aber das hebe ich mir für einen anderen Tag auf 🙂

Lassen Sie mich unten Ihre Gedanken wissen. Ich bin seit kurzem auf Twitter als ethan_the_mathmo, Sie können mir hier folgen.

Ich bin auf dieses Problem in einem wunderbaren Buch namens „The Nature of Computation“ von den Physikern Moore und Mertens gestoßen, in dem eines der Probleme durch die Analyse von Tooms Algorithmus führt.