Wenn die Daten für die Analyse bereit sind, sollte anhand einer Inspektion der Daten gründlich geprüft werden, ob statistische Methoden zur Behandlung fehlender Daten verwendet werden sollten. Bell et al. untersuchten den Umfang und den Umgang mit fehlenden Daten in randomisierten klinischen Studien, die zwischen Juli und Dezember 2013 im BMJ, JAMA, Lancet und New England Journal of Medicine veröffentlicht wurden. 95 % der 77 identifizierten Studien meldeten einige fehlende Ergebnisdaten. Die am häufigsten verwendete Methode zur Behandlung fehlender Daten in der Primäranalyse war die vollständige Fallanalyse (45 %), die einfache Imputation (27 %), modellbasierte Methoden (z. B. gemischte Modelle oder verallgemeinerte Schätzgleichungen) (19 %) und die mehrfache Imputation (8 %).
Vollständige Fallanalyse
Die vollständige Fallanalyse ist eine statistische Analyse, die auf Teilnehmern mit einem vollständigen Satz von Ergebnisdaten basiert. Teilnehmer mit fehlenden Daten werden von der Analyse ausgeschlossen. Wie in der Einleitung beschrieben, hat die vollständige Fallanalyse, wenn die fehlenden Daten MCAR sind, aufgrund der geringeren Stichprobengröße eine geringere statistische Aussagekraft, aber die beobachteten Daten werden nicht verzerrt. Handelt es sich bei den fehlenden Daten nicht um MCAR, könnte die Schätzung des Interventionseffekts der vollständigen Fallanalyse zugrunde liegen, d. h. es besteht häufig die Gefahr, dass der Nutzen überschätzt und der Schaden unterschätzt wird. Eine ausführlichere Diskussion der potenziellen Validität bei Anwendung der vollständigen Fallanalyse finden Sie im Abschnitt „Sollte die multiple Imputation zur Behandlung fehlender Daten verwendet werden?“
Einfache Imputation
Bei der einfachen Imputation werden fehlende Werte durch einen nach einer bestimmten Regel definierten Wert ersetzt. Es gibt viele Formen der einfachen Imputation, z. B. die vorgezogene letzte Beobachtung (die fehlenden Werte eines Teilnehmers werden durch den letzten beobachteten Wert des Teilnehmers ersetzt), die vorgezogene schlechteste Beobachtung (die fehlenden Werte eines Teilnehmers werden durch den schlechtesten beobachteten Wert des Teilnehmers ersetzt) und die einfache Mittelwert-Imputation . Bei der einfachen Mittelwert-Imputation werden die fehlenden Werte durch den Mittelwert der jeweiligen Variablen ersetzt. Die Verwendung einer einfachen Imputation führt häufig zu einer Unterschätzung der Variabilität, da jeder unbeobachtete Wert in der Analyse das gleiche Gewicht hat wie die bekannten, beobachteten Werte. Die Gültigkeit der einfachen Imputation hängt nicht davon ab, ob die Daten MCAR sind; die einfache Imputation hängt vielmehr von bestimmten Annahmen ab, dass die fehlenden Werte z. B. mit dem letzten beobachteten Wert identisch sind. Diese Annahmen sind oft unrealistisch, und die einfache Imputation ist daher oft eine potenziell verzerrte Methode und sollte mit großer Vorsicht angewendet werden.
Mehrfache Imputation
Die mehrfache Imputation hat sich als allgemein gültige Methode für den Umgang mit fehlenden Daten in randomisierten klinischen Studien erwiesen, und diese Methode ist für die meisten Arten von Daten verfügbar. In den folgenden Abschnitten wird beschrieben, wann und wie die multiple Imputation verwendet werden sollte.
Sollte die multiple Imputation zur Behandlung fehlender Daten verwendet werden?
Gründe, warum die multiple Imputation nicht zur Behandlung fehlender Daten verwendet werden sollte
Ist es zulässig, fehlende Daten zu ignorieren?
Bei der Analyse beobachteter Daten (vollständige Fallanalyse) ist das Ignorieren der fehlenden Daten unter drei Umständen eine gültige Lösung.
- a)
Die vollständige Fallanalyse kann als primäre Analyse verwendet werden, wenn der Anteil der fehlenden Daten unter ca. 5 % liegt (als Faustregel) und es unplausibel ist, dass bestimmte Patientengruppen (z. B. die sehr kranken oder die sehr „gesunden“ Teilnehmer) speziell in einer der verglichenen Gruppen zum Follow-up verloren gehen. Mit anderen Worten: Wenn die potenziellen Auswirkungen der fehlenden Daten vernachlässigbar sind, können die fehlenden Daten in der Analyse ignoriert werden. Im Zweifelsfall können Sensitivitätsanalysen für den „besten“ und „schlechtesten“ Fall durchgeführt werden: Zunächst wird ein Datensatz für das „beste“ und „schlechteste“ Szenario erstellt, bei dem davon ausgegangen wird, dass alle Teilnehmer, die in einer Gruppe (Gruppe 1) für die Nachbeobachtung verloren gegangen sind, ein positives Ergebnis hatten (z. B. kein schwerwiegendes unerwünschtes Ereignis), und dass alle Teilnehmer mit fehlenden Ergebnissen in der anderen Gruppe (Gruppe 2) ein schädliches Ergebnis hatten (z. B. ein schwerwiegendes unerwünschtes Ereignis). Dann wird ein Datensatz für das „Worst-Best-Case“-Szenario erstellt, bei dem angenommen wird, dass alle Teilnehmer, die in Gruppe 1 zur Weiterverfolgung verloren wurden, ein schädliches Ergebnis hatten und dass alle Teilnehmer, die in Gruppe 2 zur Weiterverfolgung verloren wurden, ein positives Ergebnis hatten. Bei kontinuierlichen Ergebnissen könnte ein „positives Ergebnis“ der Gruppenmittelwert plus 2 Standardabweichungen (oder 1 Standardabweichung) des Gruppenmittelwerts sein, und ein „negatives Ergebnis“ könnte der Gruppenmittelwert minus 2 Standardabweichungen (oder 1 Standardabweichung) des Gruppenmittelwerts sein. Bei dichotomisierten Daten zeigen diese Sensitivitätsanalysen für den besten und den schlechtesten Fall den Unsicherheitsbereich aufgrund fehlender Daten, und wenn dieser Bereich keine qualitativ widersprüchlichen Ergebnisse liefert, können die fehlenden Daten ignoriert werden. Bei kontinuierlichen Daten stellt die Imputation mit 2 SD einen möglichen Unsicherheitsbereich bei 95 % der beobachteten Daten dar (wenn diese normalverteilt sind).
- b)
Wenn nur die abhängige Variable fehlende Werte aufweist und Hilfsvariablen (Variablen, die nicht in der Regressionsanalyse enthalten sind, aber mit einer Variable mit fehlenden Werten korrelieren und/oder mit ihrer Fehlendenheit zusammenhängen) nicht identifiziert werden, kann die vollständige Fallanalyse als primäre Analyse verwendet werden, und es sollten keine spezifischen Methoden zur Behandlung der fehlenden Daten verwendet werden. Es werden keine zusätzlichen Informationen gewonnen, wenn z. B. eine multiple Imputation verwendet wird, aber die Standardfehler können sich aufgrund der Unsicherheit, die durch die multiple Imputation eingeführt wird, erhöhen.
- c)
Wie oben erwähnt (siehe Methoden zum Umgang mit fehlenden Daten), wäre es auch gültig, nur eine vollständige Fallanalyse durchzuführen, wenn es relativ sicher ist, dass die Daten MCAR sind (siehe Einleitung). Es ist relativ selten, dass es sicher ist, dass es sich bei den Daten um MCAR handelt. Es ist möglich, die Hypothese, dass die Daten MCAR sind, mit dem Little-Test zu testen, aber es könnte unklug sein, auf Tests aufzubauen, die sich als unbedeutend erweisen. Wenn also begründete Zweifel daran bestehen, dass die Daten MCAR sind, selbst wenn der Little-Test nicht signifikant ist (d. h. die Nullhypothese, dass die Daten MCAR sind, nicht zurückgewiesen werden kann), sollte nicht von MCAR ausgegangen werden.
Ist der Anteil der fehlenden Daten zu groß?
Wenn ein großer Anteil der Daten fehlt, sollte erwogen werden, nur die Ergebnisse der vollständigen Fallanalyse zu melden und dann die sich daraus ergebenden interpretativen Einschränkungen der Studienergebnisse klar zu erörtern. Wenn multiple Imputationen oder andere Methoden zur Behandlung fehlender Daten verwendet werden, könnte dies den Eindruck erwecken, dass die Ergebnisse der Studie bestätigend sind, was sie aber nicht sind, wenn der Anteil der fehlenden Daten erheblich ist. Wenn der Anteil der fehlenden Daten bei wichtigen Variablen sehr groß ist (z. B. mehr als 40 %), können die Studienergebnisse nur als hypothesengenerierende Ergebnisse betrachtet werden. Eine seltene Ausnahme wäre, wenn der zugrundeliegende Mechanismus hinter den fehlenden Daten als MCAR beschrieben werden kann (siehe Absatz oben).
Scheinen sowohl die MCAR- als auch die MAR-Annahme unplausibel?
Wenn die MAR-Annahme aufgrund der Merkmale der fehlenden Daten unplausibel erscheint, dann besteht bei den Studienergebnissen die Gefahr, dass die Ergebnisse aufgrund der „Verzerrung durch unvollständige Ergebnisdaten“ verfälscht werden, und keine statistische Methode kann diese mögliche Verzerrung mit Sicherheit berücksichtigen. Die Gültigkeit von Methoden zur Behandlung von MNAR-Daten setzt bestimmte Annahmen voraus, die nicht anhand von Beobachtungsdaten getestet werden können. Sensitivitätsanalysen für den besten und schlechtesten Fall können den gesamten theoretischen Unsicherheitsbereich aufzeigen, und die Schlussfolgerungen sollten auf diesen Unsicherheitsbereich bezogen werden. Die Grenzen der Analysen sollten gründlich erörtert und berücksichtigt werden.
Ist die Ergebnisvariable mit fehlenden Werten kontinuierlich und ist das analytische Modell kompliziert (z. B. mit Interaktionen)?
In dieser Situation kann man die Verwendung der direkten Maximum-Likelihood-Methode in Betracht ziehen, um die Probleme der Modellkompatibilität zwischen dem analytischen Modell und dem Modell der multiplen Imputation zu vermeiden, wenn Ersteres allgemeiner ist als Letzteres. Im Allgemeinen können direkte Maximum-Likelihood-Methoden verwendet werden, aber unseres Wissens sind kommerziell verfügbare Methoden derzeit nur für kontinuierliche Variablen verfügbar.
Wann und wie sollten Mehrfach-Imputationen verwendet werden
Wenn keiner der oben genannten „Gründe, warum Mehrfach-Imputationen nicht zur Behandlung fehlender Daten verwendet werden sollten“, erfüllt ist, könnte die Mehrfach-Imputation verwendet werden. In der Literatur wurden in den letzten Jahrzehnten verschiedene Verfahren für den Umgang mit fehlenden Daten vorgeschlagen. Wir haben die oben erwähnten Überlegungen zu statistischen Methoden für den Umgang mit fehlenden Daten in Abb. 1 dargestellt.
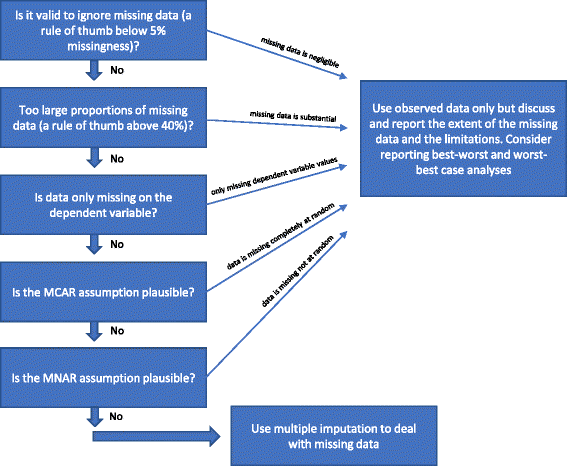
Flussdiagramm: Wann sollte die multiple Imputation zur Behandlung fehlender Daten bei der Analyse von Ergebnissen randomisierter klinischer Studien verwendet werden
Die multiple Imputation hat ihren Ursprung in den frühen 1970er Jahren und hat im Laufe der Jahre an Popularität gewonnen. Die mehrfache Imputation ist eine simulationsbasierte statistische Technik zur Behandlung fehlender Daten. Die Mehrfach-Imputation besteht aus drei Schritten:
-
Imputationsschritt. Eine „Imputation“ stellt im Allgemeinen einen Satz plausibler Werte für fehlende Daten dar – eine multiple Imputation stellt mehrere Sätze plausibler Werte dar. Bei der multiplen Imputation werden fehlende Werte identifiziert und durch eine Zufallsstichprobe plausibler Imputationswerte (vollständige Datensätze) ersetzt. Mehrere vervollständigte Datensätze werden durch ein ausgewähltes Imputationsmodell erzeugt. Fünf imputierte Datensätze werden traditionell aus theoretischen Gründen als ausreichend angesehen, aber 50 Datensätze (oder mehr) scheinen vorzuziehen, um die Stichprobenvariabilität des Imputationsprozesses zu verringern.
-
Schritt der Analyse (Schätzung) der vervollständigten Daten. Die gewünschte Analyse wird für jeden Datensatz, der während des Imputationsschrittes erzeugt wird, separat durchgeführt. Dabei werden z. B. 50 Analyseergebnisse erstellt.
-
Pooling-Schritt. Die Ergebnisse der einzelnen abgeschlossenen Datenanalysen werden zu einem einzigen Mehrfach-Imputationsergebnis zusammengefasst. Es ist nicht notwendig, eine gewichtete Metaanalyse durchzuführen, da alle 50 Analyseergebnisse das gleiche statistische Gewicht haben.
Es ist von großer Bedeutung, dass entweder eine Kompatibilität zwischen dem Imputationsmodell und dem Analysemodell besteht oder dass das Imputationsmodell allgemeiner ist als das Analysemodell (z. B. dass das Imputationsmodell mehr unabhängige Kovariaten umfasst als das Analysemodell). Wenn das Analysemodell beispielsweise signifikante Wechselwirkungen aufweist, sollte das Imputationsmodell diese ebenfalls einbeziehen, wenn das Analysemodell eine transformierte Version einer Variable verwendet, sollte das Imputationsmodell die gleiche Transformation verwenden usw.
Es gibt verschiedene Arten der multiplen Imputation
Es gibt verschiedene Arten von Methoden der multiplen Imputation. Wir werden sie nach ihrem zunehmenden Komplexitätsgrad vorstellen: 1) Einzelwert-Regressionsanalyse; 2) monotone Imputation; 3) verkettete Gleichungen oder die Markov-Chain-Monte-Carlo-Methode (MCMC). In den folgenden Abschnitten werden diese verschiedenen multiplen Imputationsmethoden beschrieben und es wird erläutert, wie man zwischen ihnen wählen kann.
Eine Einzelwert-Regressionsanalyse umfasst eine abhängige Variable und die bei der Randomisierung verwendeten Stratifikationsvariablen. Zu den Stratifikationsvariablen gehören häufig ein Zentrumsindikator, wenn es sich um eine multizentrische Studie handelt, und in der Regel eine oder mehrere Anpassungsvariablen mit prognostischen Informationen, die mit dem Ergebnis korreliert sind. Bei Verwendung einer kontinuierlichen abhängigen Variable kann auch ein Basislinienwert der abhängigen Variable einbezogen werden. Wie unter „Gründe, warum keine statistischen Methoden zur Behandlung fehlender Daten verwendet werden sollten“ erwähnt, sollte eine vollständige Fallanalyse durchgeführt werden, wenn nur die abhängige Variable fehlende Werte aufweist und keine Hilfsvariablen identifiziert wurden, und es sollten keine spezifischen Methoden zur Behandlung der fehlenden Daten verwendet werden. Wenn Hilfsvariablen identifiziert wurden, kann eine Imputation einer einzelnen Variable durchgeführt werden. Wenn die Basisvariable einer kontinuierlichen Variable signifikant fehlt, kann eine vollständige Fallanalyse verzerrte Ergebnisse liefern. Daher wird in jedem Fall eine Imputation mit einer einzigen Variable (gegebenenfalls mit oder ohne Einbeziehung von Hilfsvariablen) durchgeführt, wenn nur die Basislinienvariable fehlt.
Wenn sowohl die abhängige Variable als auch die Basislinienvariable fehlen und die Missingness monoton ist, wird eine monotone Imputation durchgeführt. Nehmen wir eine Datenmatrix an, in der die Patienten durch Zeilen und die Variablen durch Spalten dargestellt werden. Die Missingness einer solchen Datenmatrix wird als monoton bezeichnet, wenn ihre Spalten so umgeordnet werden können, dass für jeden Patienten (a) bei einem fehlenden Wert alle Werte rechts von seiner Position ebenfalls fehlen, und (b) bei einem beobachteten Wert alle Werte links von diesem Wert ebenfalls beobachtet werden. Wenn die Missingness monoton ist, ist die Methode der multiplen Imputation ebenfalls relativ einfach, selbst wenn mehr als eine Variable fehlende Werte aufweist. In diesem Fall ist es relativ einfach, die fehlenden Daten mit Hilfe der sequentiellen Regressionsimputation zu imputieren, bei der die fehlenden Werte für jede Variable auf einmal imputiert werden. Viele Statistikpakete (z. B. STATA) können analysieren, ob die Missingness monoton ist oder nicht.
Wenn die Missingness nicht monoton ist, wird eine multiple Imputation unter Verwendung der verketteten Gleichungen oder der MCMC-Methode durchgeführt. Hilfsvariablen werden in das Modell aufgenommen, wenn sie verfügbar sind. Wie zwischen den verschiedenen Methoden der multiplen Imputation zu wählen ist, haben wir in Abb. 2 zusammengefasst.
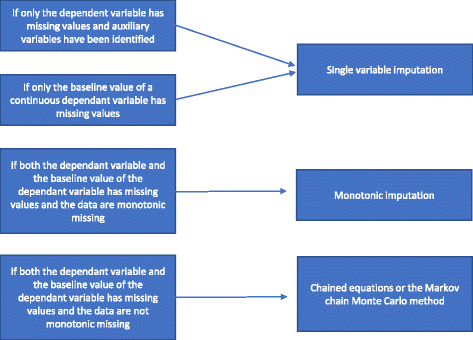
Flussdiagramm der multiplen Imputation
Full information maximum likelihood
Full information maximum likelihood ist eine alternative Methode für den Umgang mit fehlenden Daten . Das Prinzip der Maximum-Likelihood-Schätzung besteht darin, Parameter der gemeinsamen Verteilung von Ergebnis (Y) und Kovariaten (X1,…, Xk) zu schätzen, die, wenn sie wahr wären, die Wahrscheinlichkeit maximieren würden, die tatsächlich beobachteten Werte zu beobachten. Wenn bei einem bestimmten Patienten Werte fehlen, können wir die Wahrscheinlichkeit erhalten, indem wir die übliche Wahrscheinlichkeit über alle möglichen Werte der fehlenden Daten summieren, sofern der Mechanismus der fehlenden Daten ignorierbar ist. Diese Methode wird als Maximum-Likelihood-Methode mit vollständiger Information bezeichnet.
Full Information Maximum Likelihood hat im Vergleich zur multiplen Imputation sowohl Stärken als auch Grenzen.
Stärken von Full Information Maximum Likelihood im Vergleich zur multiplen Imputation
- 1)
Es ist einfacher zu implementieren, d.h. Es ist nicht notwendig, verschiedene Schritte wie bei der multiplen Imputation zu durchlaufen.
- 2)
Im Gegensatz zur multiplen Imputation gibt es bei der Full Information Maximum Likelihood keine potenziellen Probleme mit der Inkompatibilität zwischen dem Imputationsmodell und dem Analysemodell (siehe ‚Multiple Imputation‘). Die Gültigkeit der Ergebnisse der multiplen Imputation wird in Frage gestellt, wenn eine Inkompatibilität zwischen dem Imputationsmodell und dem Analysemodell besteht oder wenn das Imputationsmodell weniger allgemein ist als das Analysemodell.
- 3)
Bei der multiplen Imputation werden alle fehlenden Werte in jedem generierten Datensatz (Imputationsschritt) durch eine Zufallsstichprobe von plausiblen Werten ersetzt. Daher werden bei jeder Analyse mit multipler Imputation andere Ergebnisse angezeigt, es sei denn, es wird ein „zufälliger Seed“ angegeben. Analysen unter Verwendung der Maximum-Likelihood-Methode mit vollständiger Information für denselben Datensatz führen bei jeder Durchführung der Analyse zu denselben Ergebnissen und sind daher nicht von einem Zufallswert abhängig. Dieses Problem kann jedoch gelöst werden, wenn der Zufallswert im statistischen Analyseplan festgelegt wird.
Grenzen der vollständigen Informationsmaximallikelihood im Vergleich zur multiplen Imputation
Die Grenzen der Verwendung der vollständigen Informationsmaximallikelihood im Vergleich zur multiplen Imputation bestehen darin, dass die Verwendung der vollständigen Informationsmaximallikelihood nur mit einer speziell entwickelten Software möglich ist. Es wurde zwar eine vorläufige Software entwickelt, aber die meisten von ihnen verfügen nicht über die Funktionen kommerzieller Statistiksoftware (z. B. STATA, SAS oder SPSS). In STATA (unter Verwendung des SEM-Befehls) und SAS (unter Verwendung des PROC CALIS-Befehls) ist es möglich, die Maximum-Likelihood-Methode mit vollständiger Information zu verwenden, jedoch nur bei Verwendung von kontinuierlichen abhängigen (Ergebnis-)Variablen. Für die logistische Regression und die Cox-Regression ist das einzige kommerzielle Paket, das Maximum Likelihood mit voller Information für fehlende Daten bietet, Mplus.
Eine weitere potenzielle Einschränkung bei der Verwendung von Maximum Likelihood mit voller Information ist, dass es eine zugrunde liegende Annahme der multivariaten Normalität geben kann. Dennoch sind Verstöße gegen die Annahme der multivariaten Normalität möglicherweise nicht so wichtig, so dass es akzeptabel sein könnte, binäre unabhängige Variablen in die Analyse einzubeziehen.
Wir haben in Zusatzdatei 1 ein Programm (SAS) aufgenommen, das einen vollständigen Spielzeugdatensatz mit mehreren verschiedenen Analysen dieser Daten erzeugt. Tabelle 1 und Tabelle 2 zeigen die Ausgabe und wie verschiedene Methoden, die fehlende Daten behandeln, unterschiedliche Ergebnisse produzieren.
Panelwerte-Regressionsanalyse
Paneldaten sind in der Regel in einer so genannten breiten Datendatei enthalten, bei der die erste Zeile die Variablennamen und die nachfolgenden Zeilen (eine für jeden Patienten) die entsprechenden Werte enthalten. Das Ergebnis wird durch verschiedene Variablen dargestellt – eine für jede geplante, zeitlich festgelegte Messung des Ergebnisses. Um die Daten zu analysieren, muss die Datei in eine so genannte lange Datei mit einem Datensatz pro geplanter Ergebnismessung umgewandelt werden, die den Ergebniswert, den Zeitpunkt der Messung und eine Kopie aller anderen Variablenwerte mit Ausnahme der Werte der Ergebnisvariable enthält. Um die Korrelationen innerhalb des Patienten zwischen den zeitlichen Ergebnismessungen zu erhalten, ist es üblich, eine Mehrfachimputation der Datendatei in ihrer breiten Form durchzuführen, gefolgt von einer Analyse der resultierenden Datei, nachdem sie in ihre lange Form konvertiert wurde. Proc. mixed (SAS 9.4) kann für die Analyse von kontinuierlichen Ergebniswerten und proc. glimmix (SAS 9.4) für andere Arten von Ergebnissen verwendet werden. Da diese Prozeduren die direkte Maximum-Likelihood-Methode auf die Ergebnisdaten anwenden, aber Fälle mit fehlenden Kovariatenwerten ignorieren, können die Prozeduren direkt verwendet werden, wenn nur Werte der abhängigen Variablen fehlen und keine guten Hilfsvariablen verfügbar sind. Andernfalls sollte proc. mixed oder proc. glimmix (je nachdem, welches Verfahren geeignet ist) nach einer Mehrfachimputation verwendet werden. Natürlich ist ein entsprechender Ansatz auch mit anderen Statistikpaketen möglich.
Sensitivitätsanalysen
Sensitivitätsanalysen können als eine Reihe von Analysen definiert werden, bei denen die Daten im Vergleich zur primären Analyse anders behandelt werden. Sensitivitätsanalysen können zeigen, wie Annahmen, die sich von denen der Primäranalyse unterscheiden, die Ergebnisse beeinflussen. Sensitivitätsanalysen sollten im Voraus festgelegt und im statistischen Analyseplan beschrieben werden, doch können zusätzliche post-hoc-Sensitivitätsanalysen gerechtfertigt und zulässig sein. Wenn der potenzielle Einfluss fehlender Werte unklar ist, empfehlen wir die folgenden Sensitivitätsanalysen:
-
Wir haben bereits die Verwendung von Best-Worst- und Worst-Best-Case-Sensitivitätsanalysen beschrieben, um den Unsicherheitsbereich aufgrund fehlender Daten aufzuzeigen (siehe Bewertung, ob Methoden zur Behandlung fehlender Daten verwendet werden sollten). Unsere frühere Beschreibung der Sensitivitätsanalysen für den besten und schlechtesten Fall bezog sich auf fehlende Daten zu einer dichotomen oder kontinuierlichen abhängigen Variable, aber diese Sensitivitätsanalysen können auch verwendet werden, wenn Daten zu Stratifikationsvariablen, Basiswerten usw. fehlen. Der potenzielle Einfluss fehlender Daten sollte für jede Variable getrennt bewertet werden, d. h. es sollte für jede Variable (abhängige Variable, Ergebnisindikator und Stratifizierungsvariablen) mit fehlenden Daten ein Best-Worst- und ein Worst-Best-Case-Szenario geben.
-
Wenn entschieden wird, dass z. B. multiple Imputationen verwendet werden sollten, dann sollten diese Ergebnisse das primäre Ergebnis des jeweiligen Ergebnisses sein. Jede primäre Regressionsanalyse sollte immer durch eine entsprechende Analyse der beobachteten (oder verfügbaren) Fälle ergänzt werden.
Wenn Methoden mit gemischten Effekten verwendet werden
Die Verwendung eines multizentrischen Studiendesigns wird oft notwendig sein, um eine ausreichende Anzahl von Studienteilnehmern innerhalb eines angemessenen Zeitrahmens zu rekrutieren. Ein multizentrisches Studiendesign bietet auch eine bessere Grundlage für die spätere Verallgemeinerung der Ergebnisse. Es hat sich gezeigt, dass die am häufigsten verwendeten Analysemethoden in randomisierten klinischen Studien bei einer kleinen Anzahl von Zentren (die binäre abhängige Ergebnisse analysieren) gut funktionieren. Bei einer relativ großen Anzahl von Zentren (50 oder mehr) ist es oft optimal, das Zentrum als Zufallseffekt zu verwenden und Methoden der Analyse mit gemischten Effekten einzusetzen. Auch bei der Analyse von Längsschnittdaten ist es oft sinnvoll, Methoden der Analyse mit gemischten Effekten zu verwenden. Unter bestimmten Umständen kann es sinnvoll sein, die Kovariate mit „zufälligem Effekt“ (z. B. „Zentrum“) während des Imputationsschritts als Kovariate mit festem Effekt einzubeziehen und dann während des Analyseschritts eine Analyse mit gemischten Modellen oder verallgemeinerten Schätzgleichungen (GEE) anzuwenden. Die Anwendung eines Modells mit gemischten Effekten (z. B. mit „Zentrum“ als zufälligem Effekt) bedeutet jedoch, dass die vielschichtige Struktur der Daten bei der Modellierung der Mehrfach-Imputation berücksichtigt werden muss. Derzeit gibt es keine kommerzielle Software, die dies direkt ermöglicht. Man kann jedoch das Paket REALCOME verwenden, das über eine Schnittstelle mit STATA verbunden werden kann. Die Schnittstelle exportiert die Daten mit fehlenden Werten von STATA nach REALCOM, wo die Imputation unter Berücksichtigung der Mehrebenen-Natur der Daten und unter Verwendung einer MCMC-Methode erfolgt, die kontinuierliche Variablen einschließt und durch die Verwendung eines latenten Normalmodells auch eine angemessene Behandlung diskreter Daten ermöglicht. Die imputierten Datensätze können dann mit dem STATA-Befehl „mi estimate:“ analysiert werden, der mit der Anweisung „mixed“ (für ein kontinuierliches Ergebnis) oder der Anweisung „meqrlogit“ für binäre oder ordinale Ergebnisse in STATA kombiniert werden kann. Bei der Analyse von Paneldaten kann man jedoch leicht mit einer Situation konfrontiert werden, in der die Daten drei oder mehr Ebenen umfassen, zum Beispiel Messungen innerhalb desselben Patienten (Ebene-1), Patienten innerhalb von Zentren (Ebene-2) und Zentren (Ebene-3). Um sich nicht auf ein recht kompliziertes Modell einzulassen, das zu mangelnder Konvergenz oder instabilen Standardfehlern führen kann und für das keine kommerzielle Software zur Verfügung steht, empfehlen wir, entweder den Zentreneffekt als fix zu behandeln (direkt oder nach dem Zusammenschluss kleiner Zentren zu einem oder mehreren Zentren angemessener Größe, unter Anwendung eines Verfahrens, das im statistischen Analyseplan vorgeschrieben sein muss) oder das Zentrum als Kovariate auszuschließen. Wenn die Randomisierung nach Zentren stratifiziert wurde, führt der letztgenannte Ansatz zu einer Verzerrung der Standardfehler nach oben, was zu einem etwas konservativen Testverfahren führt.