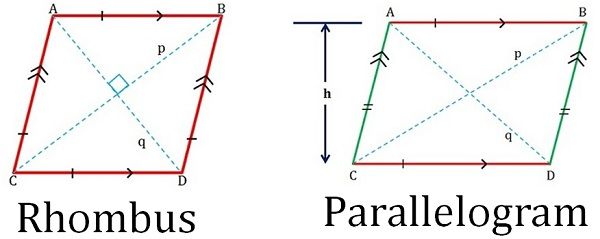
In der Geometrie gibt es viele Arten von Vierecken, z.B. Parallelogramm, Rhombus, Quadrat, Rechteck, Trapez und Drachen, die gemeinsame Merkmale haben, weshalb die Menschen Schwierigkeiten beim Verständnis dieser Figuren haben. Ein Rhombus kann als ein schräges Quadrat bezeichnet werden, dessen benachbarte Seiten gleich sind. Im Gegensatz dazu ist ein Parallelogramm ein schräges Rechteck mit zwei Sätzen paralleler gegenüberliegender Seiten.
Der grundlegende Unterschied zwischen Rhombus und Parallelogramm liegt in ihren Eigenschaften, d.h. alle Seiten eines Rhombus haben die gleiche Länge, während ein Parallelogramm eine geradlinige Figur ist, deren gegenüberliegende Seiten parallel sind.
Inhalt: Rhombus vs. Parallelogramm
- Vergleichsdiagramm
- Definition
- Schlüsselunterschiede
- Abschluss
Vergleichsdiagramm
| Vergleichsgrundlage | Rhombus | Parallelogramm |
|---|---|---|
| Bedeutung | Rhombus bezieht sich auf eine flach geformte, vierseitige Figur, bei der alle Seiten kongruent sind. | Ein Parallelogramm ist eine vierseitige, flach geformte Figur, deren gegenüberliegende Seiten parallel zueinander sind. |
| Gleiche Seiten | Alle vier Seiten sind gleich lang. | Gegenüberliegende Seiten sind gleich lang. |
| Diagonalen | Die Diagonalen halbieren sich im rechten Winkel und bilden ein skalenförmiges Dreieck. | Die Diagonalen halbieren sich und bilden zwei kongruente Dreiecke. |
| Fläche | (pq)/2, wobei p und q die Diagonalen sind | bh, wobei b = Basis und h = Höhe |
| Perimeter | 4 a, wobei a = Seite | 2 (a+b), wobei a = Seite, b = Basis |
Definition des Rhombus
Ein Viereck, dessen Seitenlängen kongruent sind, nennt man einen Rhombus. Er hat eine flache Form und vier Seiten, wobei die einander zugewandten Seiten parallel zueinander sind (siehe Abbildung unten).
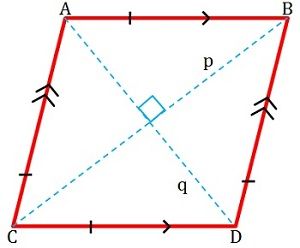Die gegenüberliegenden Winkel eines Rhombus sind gleich groß, d.h. sie haben den gleichen Grad. Seine Diagonalen treffen sich im 90-Grad-Winkel (rechter Winkel), stehen also senkrecht zueinander und bilden zwei gleichseitige Dreiecke. Die benachbarten Seiten sind komplementär, das heißt, die Summe ihrer Maße ist gleich 180 Grad. Es wird auch als gleichseitiges Parallelogramm bezeichnet.
Definition des Parallelogramms
Ein Parallelogramm ist, wie der Name schon sagt, eine flache Figur mit vier Seiten, deren gegenüberliegende Seiten parallel und kongruent sind (siehe Abbildung unten).
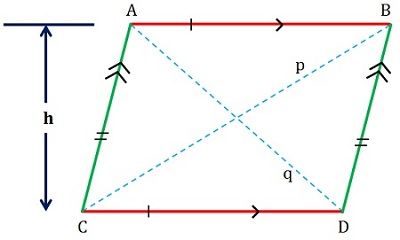Das Maß seiner gegenüberliegenden Winkel ist gleich und die aufeinanderfolgenden Winkel sind ergänzend, d.h. die Summe ihrer Maße ist gleich 180 Grad. Seine Diagonalen halbieren sich, so dass zwei kongruente Dreiecke entstehen.
Wichtige Unterschiede zwischen Rhombus und Parallelogramm
Der Unterschied zwischen Rhombus und Parallelogramm kann aus folgenden Gründen deutlich gemacht werden:
- Wir definieren den Rhombus als ein flach geformtes, vierseitiges Viereck, dessen Länge aller Seiten kongruent ist. Ein Parallelogramm ist eine vierseitige, flach geformte Figur, deren gegenüberliegende Seiten parallel zueinander sind.
- Alle Seiten des Rhombus sind gleich lang, während nur die gegenüberliegenden Seiten eines Parallelogramms gleich lang sind.
- Die Diagonalen eines Rhombus halbieren sich in rechten Winkeln und bilden zwei skalenische Dreiecke. Im Gegensatz zu einem Parallelogramm, dessen Diagonalen einander halbieren und zwei kongruente Dreiecke bilden.
- Die mathematische Formel für den Flächeninhalt des Rhombus ist (pq)/2, wobei p und q die Diagonalen sind. Umgekehrt kann der Flächeninhalt des Parallelogramms durch Multiplikation von Grundfläche und Höhe berechnet werden.
- Der Umfang des Rhombus kann mit Hilfe der folgenden Formel berechnet werden – 4 a, wobei a = Seite des Rhombus. Im Gegensatz dazu kann der Umfang des Parallelogramms berechnet werden, indem man die Basis und die Höhe addiert und die Summe mit 2 multipliziert.
Schlussfolgerung
Beide, Parallelogramm und Rhombus, sind Vierecke, deren gegenüberliegende Seiten parallel sind, die gegenüberliegenden Winkel sind gleich, die Summe der Innenwinkel beträgt 360 Grad. Die Raute selbst ist eine besondere Form des Parallelogramms. Daher kann man sagen, dass jeder Rhombus ein Parallelogramm ist, aber der umgekehrte Fall ist nicht möglich.