Understanding Activation Functions in Neural Networks

Kürzlich stellte mir ein Kollege ein paar Fragen wie „warum haben wir so viele Aktivierungsfunktionen?“, „Warum funktioniert eine besser als die andere?“, „Woher wissen wir, welche wir verwenden sollen?“, „Ist das Hardcore-Mathematik?“ und so weiter. Also dachte ich mir, warum nicht einen Artikel darüber schreiben für diejenigen, die mit neuronalen Netzen nur grundlegend vertraut sind und sich deshalb über Aktivierungsfunktionen und deren „Warum-Wie-Mathematik!“ wundern.

Hinweis: Dieser Artikel setzt voraus, dass Sie ein Grundwissen über ein künstliches „Neuron“ haben. Ich empfehle, sich vor dem Lesen dieses Artikels über die Grundlagen neuronaler Netze zu informieren, um sie besser zu verstehen.

Aktivierungsfunktionen

Was macht also ein künstliches Neuron? Einfach ausgedrückt, es berechnet eine „gewichtete Summe“ seiner Eingaben, fügt eine Vorspannung hinzu und entscheidet dann, ob es „gefeuert“ werden soll oder nicht (ja, richtig, eine Aktivierungsfunktion tut dies, aber lassen Sie uns für einen Moment mit dem Strom schwimmen).

Betrachten wir also ein Neuron.

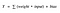
Nun kann der Wert von Y alles sein, was von -inf bis +inf reicht. Das Neuron kennt die Grenzen des Wertes nicht wirklich. Wie entscheiden wir also, ob das Neuron feuern soll oder nicht (warum dieses Feuermuster? Weil wir aus der Biologie gelernt haben, dass das Gehirn so funktioniert, und das Gehirn ist ein Arbeitszeugnis eines großartigen und intelligenten Systems).

Wir haben uns entschieden, zu diesem Zweck „Aktivierungsfunktionen“ hinzuzufügen. Um den von einem Neuron erzeugten Y-Wert zu überprüfen und zu entscheiden, ob die äußeren Verbindungen dieses Neuron als „gefeuert“ betrachten sollen oder nicht. Oder sagen wir besser – „aktiviert“ oder nicht.

Schrittfunktion

Das erste, was uns in den Sinn kommt, ist, wie wäre es mit einer schwellenbasierten Aktivierungsfunktion? Wenn der Wert von Y über einem bestimmten Wert liegt, wird er für aktiviert erklärt. Liegt er unter dem Schwellenwert, dann wird er nicht aktiviert. Hmm toll. Das könnte funktionieren!

Aktivierungsfunktion A = „aktiviert“, wenn Y > Schwellenwert, sonst nicht

Alternativ: A = 1, wenn y Schwellenwert, sonst 0

Nun, was wir gerade gemacht haben, ist eine „Stufenfunktion“, siehe die folgende Abbildung.

Ihr Ausgang ist 1 (aktiviert), wenn der Wert > 0 (Schwellenwert) ist, und gibt ansonsten eine 0 (nicht aktiviert) aus.

Gut. Das ergibt also eine Aktivierungsfunktion für ein Neuron. Keine Verwirrungen. Allerdings gibt es dabei gewisse Nachteile. Um es besser zu verstehen, denken Sie über Folgendes nach.

Angenommen, Sie erstellen einen binären Klassifikator. Etwas, das ein „Ja“ oder „Nein“ sagen soll (aktivieren oder nicht aktivieren). Eine Step-Funktion könnte das für Sie tun! Das ist genau das, was sie tut, sie sagt eine 1 oder eine 0. Denken Sie nun an den Anwendungsfall, in dem Sie mehrere solcher Neuronen verbinden möchten, um weitere Klassen einzubringen. Klasse1, Klasse2, Klasse3 usw. Was wird passieren, wenn mehr als 1 Neuron „aktiviert“ wird? Alle Neuronen werden eine 1 ausgeben (aus der Stufenfunktion). Wie würden Sie nun entscheiden? Welche Klasse ist es? Hmm schwer, kompliziert.

Sie würden wollen, dass das Netz nur 1 Neuron aktiviert und die anderen 0 sind (nur dann könnten Sie sagen, dass es die Klasse richtig klassifiziert/identifiziert hat). Ah! Das ist schwieriger zu trainieren und zu konvergieren. Es wäre besser gewesen, wenn die Aktivierung nicht binär gewesen wäre und stattdessen „50% aktiviert“ oder „20% aktiviert“ und so weiter gesagt worden wäre. Und dann, wenn mehr als 1 Neuron aktiviert ist, könnte man herausfinden, welches Neuron die „höchste Aktivierung“ hat usw. (besser als max, ein softmax, aber lassen wir das erst einmal).

Auch in diesem Fall, wenn mehr als 1 Neuron „100% aktiviert“ sagt, bleibt das Problem bestehen.Ich weiß! Aber…da es Zwischenaktivierungswerte für die Ausgabe gibt, kann das Lernen glatter und einfacher sein ( weniger wackelig ) und die Wahrscheinlichkeit, dass mehr als 1 Neuron zu 100% aktiviert ist, ist geringer, wenn man es mit der Schrittfunktion während des Trainings vergleicht ( auch abhängig davon, was man trainiert und von den Daten ).

Ok, also wollen wir etwas, das uns Zwischenaktivierungswerte ( analog ) gibt, anstatt zu sagen „aktiviert“ oder nicht ( binär ).

Das erste, was uns in den Sinn kommt, wäre eine lineare Funktion.

Lineare Funktion

A = cx

Eine geradlinige Funktion, bei der die Aktivierung proportional zur Eingabe ist ( die die gewichtete Summe der Neuronen ist ).

Auf diese Weise gibt es einen Bereich von Aktivierungen, es ist also keine binäre Aktivierung. Wir können auf jeden Fall ein paar Neuronen miteinander verbinden und wenn mehr als 1 feuert, können wir das Maximum (oder Softmax) nehmen und auf dieser Basis entscheiden. Das ist also auch in Ordnung. Wo liegt dann das Problem?

Wenn Sie mit dem Gradientenabstieg beim Training vertraut sind, werden Sie feststellen, dass bei dieser Funktion die Ableitung eine Konstante ist.

A = cx, die Ableitung nach x ist c. Das heißt, der Gradient hat keine Beziehung zu X. Es ist ein konstanter Gradient, und der Abstieg erfolgt mit konstantem Gradienten. Wenn es einen Fehler in der Vorhersage gibt, sind die Änderungen, die durch Backpropagation gemacht werden, konstant und nicht abhängig von der Änderung der Eingabe delta(x) !!!

Das ist nicht so gut! ( nicht immer, aber sei nachsichtig mit mir ). Es gibt noch ein weiteres Problem. Denken Sie an verbundene Schichten. Jede Schicht wird durch eine lineare Funktion aktiviert. Diese Aktivierung geht wiederum in die nächste Ebene als Eingabe, und die zweite Ebene berechnet eine gewichtete Summe dieser Eingabe, die wiederum auf der Grundlage einer anderen linearen Aktivierungsfunktion ausgelöst wird.

Egal wie viele Ebenen wir haben, wenn alle linear sind, ist die endgültige Aktivierungsfunktion der letzten Ebene nichts anderes als eine lineare Funktion der Eingabe der ersten Ebene! Halten Sie einen Moment inne und denken Sie darüber nach.

Das bedeutet, dass diese beiden Schichten (oder N Schichten) durch eine einzige Schicht ersetzt werden können. Ah! Auf diese Weise haben wir gerade die Fähigkeit verloren, Schichten zu stapeln. Egal wie wir stapeln, das ganze Netzwerk ist immer noch äquivalent zu einer einzelnen Schicht mit linearer Aktivierung ( eine Kombination von linearen Funktionen auf lineare Weise ist immer noch eine andere lineare Funktion ).

Lassen Sie uns weitermachen, ja?

Sigmoidfunktion

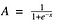
Nun, das sieht glatt und „stufenfunktionsartig“ aus. Was sind die Vorteile davon? Denken Sie einen Moment darüber nach. Zunächst einmal ist sie nichtlinearer Natur. Kombinationen dieser Funktion sind ebenfalls nichtlinear! Großartig! Jetzt können wir Schichten stapeln. Was ist mit nicht-binären Aktivierungen? Ja, auch das!. Es wird eine analoge Aktivierung im Gegensatz zur Stufenfunktion geben. Sie hat auch einen glatten Gradienten.

Und wie Sie sehen, sind die Y-Werte zwischen den X-Werten -2 bis 2 sehr steil. Das bedeutet, dass jede kleine Änderung der X-Werte in diesem Bereich zu einer deutlichen Änderung der Y-Werte führt. Das bedeutet, dass diese Funktion die Tendenz hat, die Y-Werte an die beiden Enden der Kurve zu bringen.

Sieht so aus, als ob sie in Anbetracht ihrer Eigenschaft gut für einen Klassifikator ist? Ja! Das ist sie in der Tat. Es neigt dazu, die Aktivierungen auf beide Seiten der Kurve zu bringen (zum Beispiel über x = 2 und unter x = -2). Ein weiterer Vorteil dieser Aktivierungsfunktion ist, dass im Gegensatz zur linearen Funktion die Ausgabe der Aktivierungsfunktion immer im Bereich (0,1) liegt, im Gegensatz zu (-inf, inf) der linearen Funktion. Wir haben also unsere Aktivierungen auf einen Bereich begrenzt. Schön, dann werden die Aktivierungen nicht aufgebläht.

Das ist toll. Sigmoidfunktionen sind heute eine der am häufigsten verwendeten Aktivierungsfunktionen. Wo liegen dann die Probleme?

Wie Sie sehen, reagieren die Y-Werte an den beiden Enden der Sigmoidfunktion weniger stark auf Änderungen von X. Was bedeutet das? Die Steigung in diesem Bereich wird klein sein. Daraus ergibt sich das Problem des „verschwindenden Gradienten“. Hmm. Was passiert also, wenn die Aktivierungen auf beiden Seiten in die Nähe des „fast horizontalen“ Teils der Kurve gelangen?

Der Gradient ist klein oder verschwunden (kann aufgrund des extrem kleinen Wertes keine signifikante Änderung vornehmen). Das Netz weigert sich, weiter zu lernen oder ist drastisch langsam ( je nach Anwendungsfall und bis der Gradient / die Berechnung an die Grenzen der Fließkommazahlen stößt ). Es gibt Möglichkeiten, dieses Problem zu umgehen, und Sigmoid ist bei Klassifizierungsproblemen immer noch sehr beliebt.

Tanh-Funktion

Eine weitere Aktivierungsfunktion, die verwendet wird, ist die tanh-Funktion.

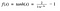
Hm. Das sieht dem Sigmoid sehr ähnlich. Tatsächlich handelt es sich um eine skalierte Sigmoidfunktion!

Ok, jetzt hat diese Funktion ähnliche Eigenschaften wie das oben besprochene Sigmoid. Es ist von Natur aus nichtlinear, so großartig, dass wir Schichten stapeln können! Es ist an den Bereich (-1, 1) gebunden, so dass man sich keine Sorgen machen muss, dass die Aktivierungen explodieren. Zu erwähnen ist, dass der Gradient bei tanh stärker ist als bei sigmoid (die Ableitungen sind steiler). Die Entscheidung zwischen sigmoid und tanh hängt von Ihren Anforderungen an die Gradientenstärke ab. Wie sigmoid hat auch tanh das Problem des verschwindenden Gradienten.

Tanh ist ebenfalls eine sehr beliebte und weit verbreitete Aktivierungsfunktion.

ReLu

Später kommt die ReLu-Funktion,

A(x) = max(0,x)

Die ReLu-Funktion ist wie oben dargestellt. Sie gibt eine Ausgabe x, wenn x positiv ist, und sonst 0.

Auf den ersten Blick sieht es so aus, als hätte sie die gleichen Probleme wie eine lineare Funktion, da sie auf der positiven Achse linear ist. Zunächst einmal ist ReLu von Natur aus nichtlinear. Und Kombinationen von ReLu sind ebenfalls nicht linear! ( in der Tat ist es ein guter Approximator. Jede Funktion kann mit Kombinationen von ReLu approximiert werden). Großartig, das bedeutet also, dass wir Schichten stapeln können. Sie ist jedoch nicht begrenzt. Der Bereich von ReLu ist [0, inf). Das bedeutet, dass es die Aktivierung aufblähen kann.

Ein weiterer Punkt, den ich hier diskutieren möchte, ist die Spärlichkeit der Aktivierung. Stellen Sie sich ein großes neuronales Netzwerk mit vielen Neuronen vor. Die Verwendung eines Sigmoid oder Tanh führt dazu, dass fast alle Neuronen auf analoge Weise feuern (Sie erinnern sich?). Das bedeutet, dass fast alle Aktivierungen verarbeitet werden, um die Ausgabe eines Netzes zu beschreiben. Mit anderen Worten, die Aktivierung ist sehr dicht. Das ist kostspielig. Idealerweise würden wir wollen, dass einige Neuronen im Netz nicht aktiviert werden, um die Aktivierungen spärlich und effizient zu machen.

ReLu bietet uns diesen Vorteil. Stellen Sie sich ein Netzwerk mit zufällig initialisierten Gewichten ( oder normalisiert ) vor und fast 50% des Netzwerks ergibt 0 Aktivierung aufgrund der Eigenschaft von ReLu ( Ausgabe 0 für negative Werte von x ). Das bedeutet, dass weniger Neuronen feuern ( spärliche Aktivierung ) und das Netz leichter ist. Wow, schön! ReLu scheint großartig zu sein! Ja, das ist es, aber nichts ist makellos… Nicht einmal ReLu.

Aufgrund der horizontalen Linie in ReLu (für negatives X) kann der Gradient gegen 0 gehen. Für Aktivierungen in dieser Region von ReLu wird der Gradient 0 sein, weshalb die Gewichte während des Abstiegs nicht angepasst werden. Das bedeutet, dass die Neuronen, die sich in diesem Zustand befinden, nicht mehr auf Veränderungen des Fehlers/der Eingabe reagieren (einfach weil der Gradient 0 ist, ändert sich nichts). Dies wird als sterbendes ReLu-Problem bezeichnet. Dieses Problem kann dazu führen, dass mehrere Neuronen einfach absterben und nicht mehr reagieren, wodurch ein wesentlicher Teil des Netzes passiv wird. Es gibt Variationen in ReLu, um dieses Problem zu entschärfen, indem die horizontale Linie einfach in eine nicht-horizontale Komponente umgewandelt wird. z.B. y = 0.01x für x<0 macht es zu einer leicht geneigten Linie anstatt einer horizontalen Linie. Dies ist undichte ReLu. Es gibt auch andere Varianten. Die Hauptidee ist, dass der Gradient nicht Null ist und sich während des Trainings erholt.

ReLu ist weniger rechenaufwändig als tanh und sigmoid, weil es einfachere mathematische Operationen beinhaltet. Das ist ein guter Punkt, den man berücksichtigen sollte, wenn man tiefe neuronale Netze entwirft.

Ok, welche benutzen wir jetzt?

Nun, welche Aktivierungsfunktionen sollen wir benutzen. Heißt das, dass wir für alles, was wir tun, nur ReLu verwenden? Oder sigmoid oder tanh? Nun, ja und nein. Wenn man weiß, dass die Funktion, die man zu approximieren versucht, bestimmte Eigenschaften hat, kann man eine Aktivierungsfunktion wählen, die die Funktion schneller approximiert, was zu einem schnelleren Trainingsprozess führt. Ein Sigmoid zum Beispiel eignet sich gut für einen Klassifikator (siehe die Grafik des Sigmoid, zeigt sie nicht die Eigenschaften eines idealen Klassifikators? ), denn die Annäherung einer Klassifikatorfunktion als Kombinationen von Sigmoiden ist einfacher als z. B. ReLu. Dies führt zu einem schnelleren Trainingsprozess und einer schnelleren Konvergenz. Sie können auch Ihre eigenen benutzerdefinierten Funktionen verwenden! Wenn Sie die Art der Funktion, die Sie zu lernen versuchen, nicht kennen, würde ich vorschlagen, mit ReLu zu beginnen und dann rückwärts zu arbeiten. ReLu funktioniert die meiste Zeit als allgemeiner Approximator!

In diesem Artikel habe ich versucht, ein paar häufig verwendete Aktivierungsfunktionen zu beschreiben. Es gibt auch andere Aktivierungsfunktionen, aber die allgemeine Idee bleibt die gleiche. Die Forschung nach besseren Aktivierungsfunktionen ist noch nicht abgeschlossen. Ich hoffe, Sie haben die Idee hinter der Aktivierungsfunktion verstanden, warum sie verwendet werden und wie wir entscheiden, welche wir verwenden sollen.