Existem vários tipos de gráficos, dependendo do número de vértices, número de arestas, interconectividade e sua estrutura geral. Vamos discutir apenas alguns tipos importantes de gráficos neste capítulo.
Gráfico Nulo
Um gráfico sem arestas é chamado Gráfico Nulo.
Exemplo

No gráfico acima, há três vértices chamados ‘a’, ‘b’ e ‘c’, mas não há arestas entre eles. Portanto é um Gráfico Nulo.
Gráfico Trivial
Um gráfico com apenas um vértice é chamado Gráfico Trivial.
Exemplo
No gráfico acima mostrado, há apenas um vértice ‘a’ sem outras arestas. Portanto, é um gráfico Trivial.
Gráfico não direcionado
Um gráfico não direcionado contém arestas, mas as arestas não são direcionadas.
Exemplo
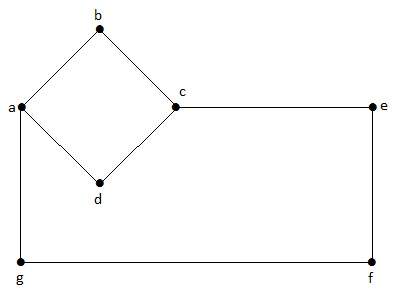
Neste gráfico, ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’ são os vértices, e ‘ab’, ‘bc’, ‘cd’, ‘da’, ‘ag’, ‘gf’, ‘ef’ são as arestas do gráfico. Como é um gráfico não direcionado, as bordas ‘ab’ e ‘ba’ são as mesmas. Similarmente outras arestas também consideradas da mesma forma.
Gráfico Direcionado
Em um gráfico direcionado, cada aresta tem uma direção.
Exemplo
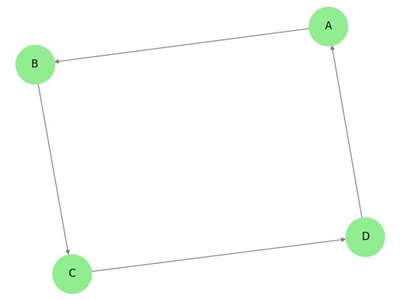
No gráfico acima, temos sete vértices ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, e ‘g’, e oito arestas ‘ab’, ‘cb’, ‘dc’, ‘ad’, ‘ec’, ‘fe’, ‘gf’, e ‘ga’. Como é um gráfico dirigido, cada aresta tem uma marca de seta que mostra a sua direção. Note que em um gráfico dirigido, ‘ab’ é diferente de ‘ba’.
Gráfico simples
Um gráfico sem loops e sem bordas paralelas é chamado de gráfico simples.
-
O número máximo de arestas possíveis em um único gráfico com vértices ‘n’ é nC2 onde nC2 = n(n – 1)/2.
-
O número de gráficos simples possível com ‘n’ vértices = 2nc2 = 2n(n-1)/2.
Exemplo
No gráfico seguinte, há 3 vértices com 3 arestas, que é o máximo excluindo as arestas paralelas e os loops. Isto pode ser provado usando as fórmulas acima.
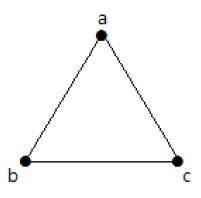
O número máximo de arestas com n=3 vértices –
nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
O número máximo de gráficos simples com n=3 vértices –
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
Estes 8 gráficos são como mostrado abaixo –
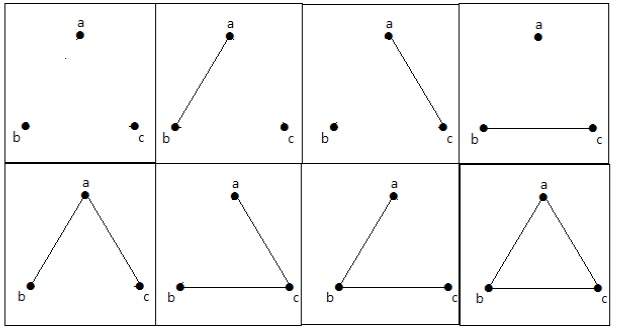
Gráfico ligado
Diz-se que um gráfico G está ligado se existir um caminho entre cada par de vértices. Deve haver pelo menos uma aresta para cada vértice do gráfico. Para que possamos dizer que ele está conectado a algum outro vértice do outro lado da aresta.
Exemplo
No gráfico seguinte, cada vértice tem a sua própria aresta conectada a outra aresta. Portanto é um gráfico conectado.
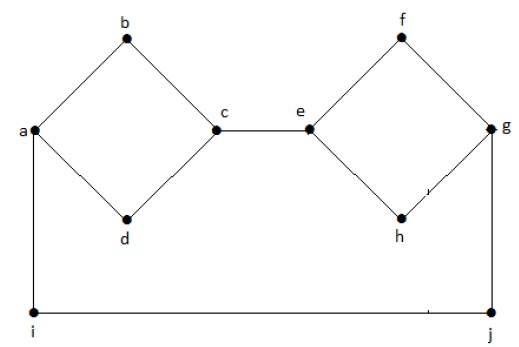
Gráfico desconectado
Um gráfico G é desconectado, se não contiver pelo menos dois vértices conectados.
Exemplo 1
O gráfico seguinte é um exemplo de um gráfico desconectado, onde há dois componentes, um com ‘a’, ‘b’, ‘c’, ‘d’ e outro com ‘e’, ‘f’, ‘g’, ‘h’ vértices.
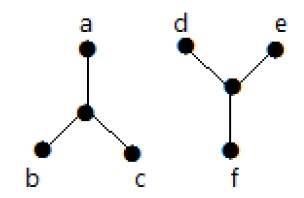
Os dois componentes são independentes e não estão conectados um ao outro. Por isso se chama gráfico desconectado.
Exemplo 2
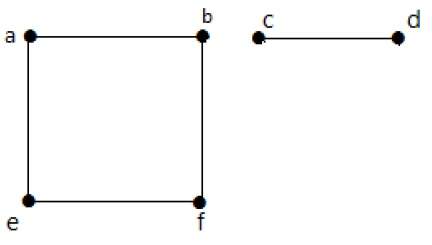
Neste exemplo, há dois componentes independentes, a-b-f-e e c-d, que não estão conectados um ao outro. Portanto, este é um gráfico desconectado.
Gráfico Regular
Diz-se que o gráfico G é regular, se todos os seus vértices tiverem o mesmo grau. Em um gráfico, se o grau de cada vértice é ‘k’, então o gráfico é chamado de ‘gráfico k-regular’.
Exemplo
Nos gráficos seguintes, todos os vértices têm o mesmo grau. Então estes gráficos são chamados de gráficos regulares.
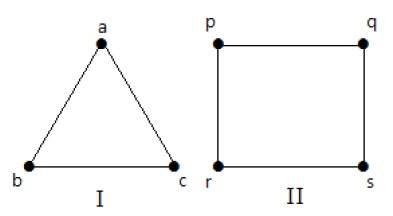
Em ambos os gráficos, todos os vértices têm o grau 2. Eles são chamados de gráficos 2-Regulares.
Gráficos Completos
Um gráfico simples com ‘n’ vértices mútuos é chamado de gráfico completo e é denotado por ‘Kn’. No gráfico, um vértice deve ter bordas com todos os outros vértices, então ele é chamado de gráfico completo.
Em outras palavras, se um vértice está conectado a todos os outros vértices de um gráfico, então ele é chamado de gráfico completo.
Exemplo
Nos gráficos seguintes, cada vértice no gráfico é conectado com todos os vértices restantes no gráfico, exceto por si só.
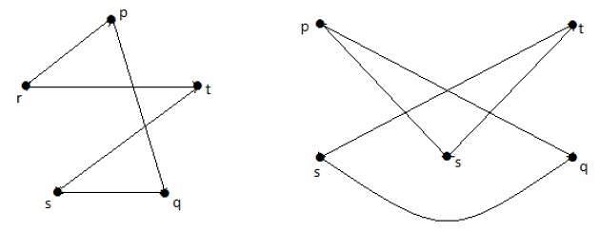
No gráfico I,
| a | b | c | |
|---|---|---|---|
| a | Não Ligado | Ligado | Ligado |
| b | Conectado | Não Ligado | Conectado |
| c | Conectado | Conectado | Não Ligado |
No gráfico II,
| p | q | r | s | |
|---|---|---|---|---|
| p | Não Ligado | Ligado | Ligado | Conectado |
| q | Conectado | Não Ligado | Conectado | Conectado |
| r | Conectado | Conectado | Não ligado | Conectado |
| s | Conectado | Conectado | Conectado | Não Connected |
Cycle Graph
Um gráfico simples com ‘n’ vértices (n >= 3) e ‘n’ arestas é chamado de gráfico de ciclo se todas as suas arestas formam um ciclo de comprimento ‘n’.
Se o grau de cada vértice do gráfico for dois, então é chamado de gráfico cíclico.
Notação – Cn
Exemplo
Dê uma olhada nos seguintes gráficos –
-
Gráfico I tem 3 vértices com 3 arestas que está formando um ciclo ‘ab-bc-ca’.
-
Graph II tem 4 vértices com 4 arestas que está formando um ciclo ‘pq-qs-sr-rp’.
-
Graph III tem 5 vértices com 5 arestas que está formando um ciclo ‘ik-km-ml-lj-ji’.
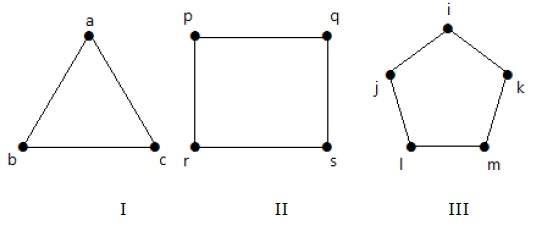
Hence todos os gráficos dados são gráficos de ciclo.
Gráficos de roda
Um gráfico de roda é obtido a partir de um gráfico de ciclo Cn-1, adicionando um novo vértice. Esse novo vértice é chamado de Hub que é conectado a todos os vértices do Cn.
Notação – Wn
No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)
Exemplo
Dê uma olhada nos seguintes gráficos. São todos gráficos de roda.
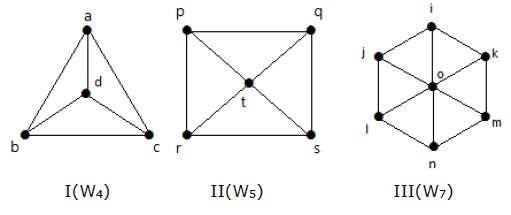
No gráfico I, é obtido a partir de C3 adicionando um vértice no meio chamado ‘d’. É denotado como W4.
Number of edges in W4 = 2(n-1) = 2(3) = 6
No gráfico II, é obtido a partir de C4 adicionando um vértice no meio nomeado como ‘t’. É denotado como W5.
Number of edges in W5 = 2(n-1) = 2(4) = 8
No gráfico III, é obtido a partir de C6 adicionando um vértice no meio nomeado como ‘o’. É denotado como W7.
Number of edges in W4 = 2(n-1) = 2(6) = 12
Gráfico cíclico
Um gráfico com pelo menos um ciclo é chamado de gráfico cíclico.
Exemplo
No gráfico de exemplo acima, temos dois ciclos a-b-c-d-a e c-f-g-e-c. Assim é chamado um gráfico cíclico.
Gráfico acíclico
Um gráfico sem ciclos é chamado de gráfico acíclico.
Exemplo
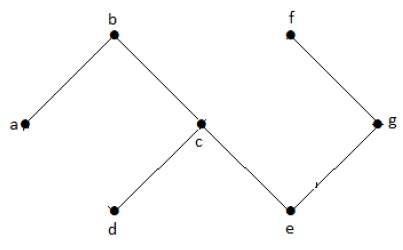
No gráfico do exemplo acima, não temos nenhum ciclo. Portanto é um gráfico não cíclico.
Gráfico bipartido
Um gráfico simples G = (V, E) com partição de vértices V = {V1, V2} é chamado de gráfico bipartido se cada borda de E junta um vértice em V1 a um vértice em V2.
Em geral, um gráfico Bipertite tem dois conjuntos de vértices, digamos, V1 e V2, e se uma aresta é desenhada, ela deve conectar qualquer vértice do conjunto V1 a qualquer vértice do conjunto V2.
Exemplo
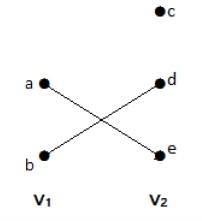
Neste gráfico, você pode observar dois conjuntos de vértices – V1 e V2. Aqui, duas arestas chamadas ‘ae’ e ‘bd’ estão conectando os vértices de dois conjuntos V1 e V2.
Gráfico bipartido completo
Um gráfico bipartido ‘G’, G = (V, E) com partição V = {V1, V2} é dito ser um gráfico bipartido completo se cada vértice em V1 estiver conectado a cada vértice de V2.
Em geral, um gráfico bipartido completo liga cada vértice do conjunto V1 a cada vértice do conjunto V2.
Exemplo
O gráfico seguinte é um gráfico bipartido completo porque tem bordas conectando cada vértice do conjunto V1 a cada vértice do conjunto V2.
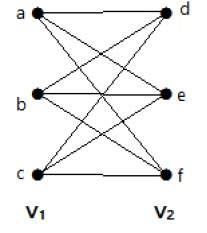
Se |V1| = m e |V2| = n, então o gráfico bipartido completo é denotado por Km, n.
-
Km,n tem (m+n) vértices e (mn) bordas.
-
Km,n é um gráfico regular se m=n.
Em geral, um gráfico bipartido completo não é um gráfico completo.
Km,n é um gráfico completo se m=n=1.
O número máximo de bordas em um gráfico bipartido com n vértices é
Se n=10, k5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25
Similiarmente K6, 4=24
K7, 3=21
K8, 2=16
K9, 1=9
If n=9, k5, 4 = 4⌋/4⌋ = 4⌋/4⌋ = 20
Similiarmente K6, 3=18
K7, 2=14
K8, 1=8
‘G’ é um gráfico bipartido se ‘G’ não tiver ciclos de comprimento ímpar. Um caso especial de gráfico bipartido é um gráfico estrelado.
Gráfico estrelado
Um gráfico bipartido completo da forma K1, n-1 é um gráfico estrelado com n-vertices. Um gráfico estelar é um gráfico bipartido completo se um único vértice pertence a um conjunto e todos os vértices restantes pertencem ao outro conjunto.
Exemplo
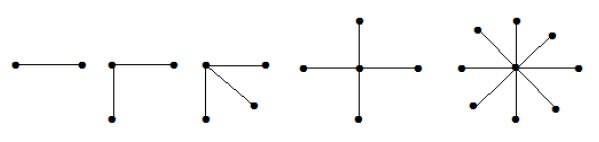
Nos gráficos acima, de ‘n’ vértices, todos os vértices ‘n-1’ estão ligados a um único vértice. Portanto, está na forma de K1, n-1 que são gráficos estelares.
Complemento de um Gráfico
Deixe ‘G-‘ ser um gráfico simples com alguns vértices como o de ‘G’ e uma aresta {U, V} está presente em ‘G-‘, se a aresta não estiver presente em G. Isto significa que dois vértices estão adjacentes em ‘G-‘ se os dois vértices não estiverem adjacentes em G.
Se as arestas que existem no gráfico I estiverem ausentes em outro gráfico II, e se ambos os gráficos I e II estiverem combinados para formar um gráfico completo, então o gráfico I e o gráfico II são chamados de complementos um do outro.
Exemplo
No exemplo seguinte, o gráfico I tem duas arestas ‘cd’ e ‘bd’. Seu gráfico complementar-II tem quatro arestas.
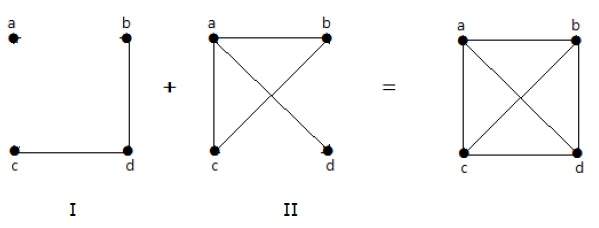
Notem que as arestas no gráfico-I não estão presentes no gráfico-II e vice versa. Portanto, a combinação dos dois gráficos dá um gráfico completo de ‘n’ vértices.
Nota – Uma combinação de dois gráficos complementares dá um gráfico completo.
Se ‘G’ é qualquer gráfico simples, então
|E(G)| + |E(‘G-‘)| = |E(Kn)|, onde n = número de vértices no gráfico.
Exemplo
Deixe ‘G’ ser um gráfico simples com nove vértices e doze arestas, encontre o número de arestas em ‘G-‘.
Você tem, |E(G)| + |E(‘G-‘)| = |E(Kn)|
12 + |E(‘G-‘)| =