Quando os dados estão prontos para serem analisados, deve ser cuidadosamente avaliado, com base na inspecção dos dados, se devem ser usados métodos estatísticos para lidar com dados ausentes. Bell et al. tiveram como objectivo avaliar a extensão e o tratamento dos dados em falta em ensaios clínicos aleatórios publicados entre Julho e Dezembro de 2013 no BMJ, JAMA, Lancet, e New England Journal of Medicine . 95% dos 77 ensaios identificados reportaram alguns dados de resultados em falta. O método mais comumente utilizado para lidar com dados ausentes na análise primária foi a análise de casos completa (45%), imputação única (27%), métodos baseados em modelos (por exemplo, modelos mistos ou equações de estimação generalizada) (19%) e imputação múltipla (8%) .
Análise de casos completa
Análise de casos completa é a análise estatística baseada em participações com um conjunto completo de dados de resultados. Os participantes com quaisquer dados em falta são excluídos da análise. Como descrito na introdução, se os dados em falta forem MCAR a análise de casos completa terá um poder estatístico reduzido devido ao tamanho reduzido da amostra, mas os dados observados não serão tendenciosos . Quando os dados em falta não são MCAR, a estimativa completa da análise de caso do efeito da intervenção pode ser baseada, ou seja, muitas vezes haverá um risco de sobrestimação do benefício e subestimação do dano . Por favor veja a seção ‘Deve-se usar imputação múltipla para lidar com dados ausentes?’ para uma discussão mais detalhada da validade potencial se a análise de caso completa for aplicada.
Atribuição única
Quando se usa imputação única, os valores ausentes são substituídos por um valor definido por uma determinada regra . Existem muitas formas de imputação única, por exemplo, a última observação transportada (os valores em falta de um participante são substituídos pelo último valor observado do participante), a pior observação transportada (os valores em falta de um participante são substituídos pelo pior valor observado do participante), e a imputação média simples . Na imputação média simples, os valores em falta são substituídos pela média dessa variável . A utilização de uma única imputação resulta frequentemente numa subestimação da variabilidade porque cada valor não observado tem o mesmo peso na análise que os valores conhecidos e observados . A validade da imputação única não depende se os dados são MCAR; a imputação única depende mais de suposições específicas de que os valores em falta, por exemplo, são idênticos ao último valor observado . Estas suposições são frequentemente irrealistas e a imputação única é, portanto, frequentemente um método potencialmente tendencioso e deve ser usado com grande cuidado .
Atribuição múltipla
Atribuição múltipla demonstrou ser um método geral válido para lidar com dados em falta em ensaios clínicos aleatórios, e este método está disponível para a maioria dos tipos de dados . Nas secções seguintes iremos descrever quando e como a imputação múltipla deve ser usada.
Deve ser usada a imputação múltipla para lidar com dados em falta?
Razões pelas quais a imputação múltipla não deve ser usada para lidar com dados em falta
É válido ignorar dados em falta?
Análise dos dados observados (análise completa do caso) ignorando os dados em falta é uma solução válida em três circunstâncias.
- a)
Análise de casos completa pode ser usada como análise primária se as proporções de dados ausentes estiverem abaixo de aproximadamente 5% (como regra geral) e for implausível que certos grupos de pacientes (por exemplo, os muito doentes ou os participantes muito “bem”) especificamente se percam para acompanhamento em um dos grupos comparados. Em outras palavras, se o impacto potencial dos dados em falta for insignificante, então os dados em falta podem ser ignorados na análise . As melhores e piores análises de sensibilidade aos casos podem ser usadas em caso de dúvida: primeiro é gerado um conjunto de dados do cenário “melhor caso” onde se assume que todos os participantes perdidos para acompanhamento em um grupo (referido como grupo 1) tiveram um resultado benéfico (por exemplo, não tiveram nenhum evento adverso grave); e todos aqueles com resultados ausentes no outro grupo (grupo 2) tiveram um resultado prejudicial (por exemplo, tiveram um evento adverso grave) . Em seguida, é gerado um conjunto de dados do cenário “pior caso” onde se assume que todos os participantes perdidos para acompanhamento no grupo 1 tiveram um desfecho prejudicial; e que todos aqueles perdidos para acompanhamento no grupo 2 tiveram um desfecho benéfico . Se forem usados resultados contínuos, então um ‘resultado benéfico’ pode ser a média do grupo mais 2 desvios padrão (ou 1 desvio padrão) da média do grupo, e um ‘resultado prejudicial’ pode ser a média do grupo menos 2 desvios padrão (ou 1 desvio padrão) da média do grupo . Para os dados dicotomizados, essas análises de sensibilidade de melhores e piores casos mostrarão o intervalo de incerteza devido à falta de dados e, se esse intervalo não fornecer resultados qualitativamente contraditórios, então os dados em falta poderão ser ignorados. Para a imputação contínua de dados com 2 DP representará um possível intervalo de incerteza dado que 95% dos dados observados (se normalmente distribuídos).
- b)
Se apenas a variável dependente tiver valores ausentes e variáveis auxiliares (variáveis não incluídas na análise de regressão, mas correlacionadas com uma variável com valores ausentes e/ou relacionadas à sua falta) não forem identificadas, a análise de casos completa pode ser usada como análise primária e nenhum método específico deve ser usado para lidar com os dados ausentes . Nenhuma informação adicional será obtida, por exemplo, usando imputação múltipla, mas os erros padrão podem aumentar devido à incerteza introduzida pela imputação múltipla .
- c)
Como mencionado acima (ver Métodos para lidar com dados ausentes), também seria válido apenas para realizar uma análise de caso completa se for relativamente certo que os dados são MCAR (ver Introdução). É relativamente raro que haja a certeza de que os dados são MCAR. É possível testar a hipótese de que os dados são MCAR com o teste de Little , mas pode não ser sensato construir com base em testes que se revelaram insignificantes. Portanto, se houver dúvida razoável se os dados são MCAR, mesmo que o teste de Little seja insignificante (não rejeitar a hipótese nula de que os dados são MCAR), então MCAR não deve ser assumido.
As proporções de dados em falta são muito grandes?
Se grandes proporções de dados estão em falta, deve ser considerado apenas para relatar os resultados da análise completa do caso e, em seguida, discutir claramente as limitações interpretativas resultantes dos resultados do estudo. Se forem usadas múltiplas imputações ou outros métodos para lidar com dados ausentes, isso pode indicar que os resultados do estudo são confirmativos, o que não acontece se a falta de dados for considerável. Se as proporções de dados em falta forem muito grandes (por exemplo, mais de 40%) em variáveis importantes, então os resultados do estudo só podem ser considerados como hipóteses geradoras de resultados. Uma exceção rara seria se o mecanismo subjacente por trás dos dados em falta puder ser descrito como MCAR (ver parágrafo acima).
A suposição MCAR e MAR parecem ambos implausíveis?
Se a suposição MAR parece implausível com base nas características dos dados em falta, então os resultados do estudo estarão em risco de resultados tendenciosos devido a “viés de dados incompletos” e nenhum método estatístico pode com certeza levar em conta este viés potencial. A validade dos métodos usados para lidar com dados MNAR requer certas suposições que não podem ser testadas com base nos dados observados. As melhores e piores análises de sensibilidade aos casos podem mostrar toda a gama teórica de incerteza e as conclusões devem estar relacionadas com esta gama de incerteza. As limitações das análises devem ser cuidadosamente discutidas e consideradas.
É a variável de resultado com valores em falta contínua e o modelo analítico é complicado (por exemplo, com interações)?
Nesta situação, pode-se considerar o uso do método de máxima verosimilhança direta para evitar os problemas de compatibilidade do modelo analítico com o modelo de imputação múltipla onde o primeiro é mais geral do que o segundo. Em geral, métodos de máxima verosimilhança direta podem ser usados, mas, ao nosso conhecimento, os métodos comercialmente disponíveis atualmente só estão disponíveis para variáveis contínuas.
Quando e como usar múltiplas imputações
Se nenhuma das ‘Razões pelas quais a imputação múltipla não deve ser usada para lidar com dados ausentes’ de cima for cumprida, então a imputação múltipla poderia ser usada. Vários procedimentos têm sido sugeridos na literatura nas últimas décadas para lidar com dados ausentes . Esboçamos as considerações acima mencionadas sobre métodos estatísticos para lidar com dados ausentes na Fig. 1.
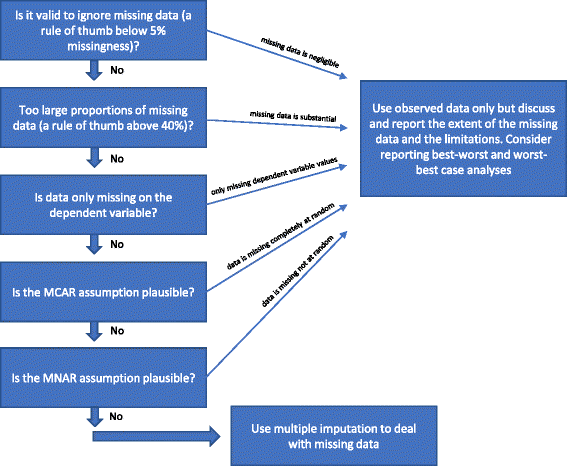
Flowchart: quando deve ser usada a imputação múltipla para lidar com dados faltantes ao analisar resultados de ensaios clínicos aleatórios
Atribuição múltipla originada no início dos anos 70, e tem ganho popularidade crescente ao longo dos anos . A imputação múltipla é uma técnica estatística baseada em simulação para lidar com dados em falta . A imputação múltipla consiste em três etapas:
-
Passo de imputação. Uma ‘imputação’ geralmente representa um conjunto de valores plausíveis para dados faltantes – imputação múltipla representa múltiplos conjuntos de valores plausíveis . Ao utilizar a imputação múltipla, os valores em falta são identificados e substituídos por uma amostra aleatória de imputações de valores plausíveis (conjuntos de dados completados). Os conjuntos de dados múltiplos completados são gerados através de algum modelo de imputação escolhido . Cinco conjuntos de dados imputados têm sido tradicionalmente sugeridos para serem suficientes em termos teóricos, mas 50 conjuntos de dados (ou mais) parecem ser preferíveis para reduzir a variabilidade da amostragem do processo de imputação .
-
Análise de dados completados (estimativa) etapa. A análise desejada é realizada separadamente para cada conjunto de dados que é gerado durante a etapa de imputação. Assim, por exemplo, são construídos 50 resultados de análise.
-
Etapa de análise. Os resultados obtidos de cada análise de dados completados são combinados em um único resultado de múltipla imputação . Não há necessidade de realizar uma meta-análise ponderada, pois todos dizem que 50 resultados de análise são considerados como tendo o mesmo peso estatístico.
É de grande importância que haja compatibilidade entre o modelo de imputação e o modelo de análise ou que o modelo de imputação seja mais geral que o modelo de análise (por exemplo, que o modelo de imputação inclua covariáveis mais independentes que o modelo de análise) . Por exemplo, se o modelo de análise tiver interações significativas, então o modelo de imputação deve incluí-las também , se o modelo de análise usar uma versão transformada de uma variável então o modelo de imputação deve usar a mesma transformação , etc.
Diferentes tipos de imputação múltipla
Existem diferentes tipos de métodos de imputação múltipla. Nós os apresentaremos de acordo com seus crescentes graus de complexidade: 1) análise de regressão de valor único; 2) imputação monotônica; 3) equações encadeadas ou o método de cadeia de Markov Monte Carlo (MCMC). Nos parágrafos seguintes descreveremos estes diferentes métodos de imputação múltipla e como escolher entre eles.
Uma análise de regressão de variável única inclui uma variável dependente e as variáveis de estratificação utilizadas na aleatorização. As variáveis de estratificação frequentemente incluem um indicador central se o estudo for um estudo multicêntrico e normalmente uma ou mais variáveis de ajuste com informações prognósticas que estão correlacionadas com o resultado. Ao usar uma variável dependente contínua, um valor basal da variável dependente também pode ser incluído. Como mencionado em “Razões pelas quais métodos estatísticos não devem ser usados para lidar com dados ausentes”, se apenas a variável dependente tiver valores ausentes e variáveis auxiliares não forem identificadas, uma análise de caso completa deve ser realizada e nenhum método específico deve ser usado para lidar com os dados ausentes. Se variáveis auxiliares tiverem sido identificadas, uma única imputação de variável pode ser realizada. Se houver uma falta significativa na variável de base de uma variável contínua, uma análise de caso completa pode fornecer resultados tendenciosos . Portanto, em todos os eventos, uma única imputação de variável (com ou sem variáveis auxiliares incluídas conforme apropriado) é realizada se apenas a variável de linha de base estiver ausente.
Se tanto a variável dependente quanto a variável de linha de base estiverem ausentes e a missingness for monótona, uma imputação monótona é feita. Assumir uma matriz de dados onde os pacientes são representados por linhas e as variáveis por colunas. A missingness de tal matriz de dados é dita monótona se suas colunas podem ser reordenadas de forma que para qualquer paciente (a) se um valor estiver faltando todos os valores à direita de sua posição também estão faltando, e (b) se um valor for observado todos os valores à esquerda desse valor também são observados . Se a missingness for monótona, o método de imputação múltipla também é relativamente simples, mesmo que mais de uma variável tenha valores em falta . Neste caso, é relativamente simples imputar os dados em falta utilizando a imputação de regressão sequencial, onde os valores em falta são imputados para cada variável de cada vez . Muitos pacotes estatísticos (por exemplo, STATA) podem analisar se a missingness é monótona ou não.
Se a missingness não é monótona, uma imputação múltipla é conduzida usando as equações encadeadas ou o método MCMC. As variáveis auxiliares são incluídas no modelo, caso estejam disponíveis. Resumimos como escolher entre os diferentes métodos de imputação múltipla na Fig. 2.
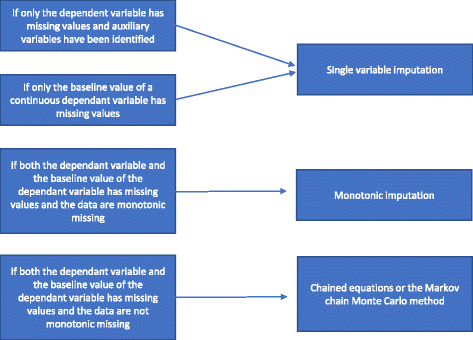
Flowchart de imputação múltipla
Previsão máxima de informação completa
Previsão máxima de informação completa é um método alternativo para lidar com dados ausentes . O princípio da estimação da máxima verosimilhança é estimar parâmetros da distribuição conjunta de resultados (Y) e covariáveis (X1,…, Xk) que, se verdadeiros, maximizariam a probabilidade de observarmos os valores que de fato observamos . Se faltam valores num determinado paciente, podemos obter a probabilidade através da soma da probabilidade habitual sobre todos os valores possíveis dos dados em falta, desde que o mecanismo de dados em falta seja ignorável. Este método é chamado de máxima verosimilhança de informação completa .
A máxima verosimilhança da informação completa tem tanto forças como limitações em comparação com a imputação múltipla.
Forças da máxima verosimilhança da informação completa em comparação com a imputação múltipla
- 1)
É mais simples de implementar, ou seja não é necessário passar por diferentes passos como quando se usa imputação múltipla.
- 2)
Impossibilidade máxima de informação não semelhante à imputação múltipla, a máxima verosimilhança de informação não tem problemas potenciais com incompatibilidade entre o modelo de imputação e o modelo de análise (ver ‘Imputação múltipla’). A validade dos resultados de imputação múltipla será questionável se houver uma incompatibilidade entre o modelo de imputação e o modelo de análise, ou se o modelo de imputação for menos geral que o modelo de análise .
- 3)
Ao utilizar imputação múltipla, todos os valores em falta em cada conjunto de dados gerados (etapa de imputação) são substituídos por uma amostra aleatória de valores plausíveis . Assim, a menos que ‘uma semente aleatória’ seja especificada, cada vez que uma análise de imputação múltipla for realizada, resultados diferentes serão mostrados . As análises quando se utiliza informação completa, a máxima probabilidade no mesmo conjunto de dados produzirá os mesmos resultados cada vez que a análise for realizada, e os resultados não dependem, portanto, de um número aleatório de semente. Entretanto, se o valor da semente aleatória for definido no plano de análise estatística este problema pode ser resolvido.
Limitações da máxima verosimilhança de informação completa em comparação com a imputação múltipla
As limitações do uso da máxima verosimilhança de informação completa em comparação com o uso da imputação múltipla, é que o uso da máxima verosimilhança de informação completa só é possível usando um software especialmente projetado. Foram desenvolvidos softwares preliminares projetados, mas a maioria deles carece das características de softwares estatísticos projetados comercialmente (por exemplo, STATA, SAS, ou SPSS). Em STATA (usando o comando SEM) e SAS (usando o comando PROC CALIS), é possível usar a máxima probabilidade de informação completa, mas apenas quando se usam variáveis contínuas dependentes (resultado). Para regressão logística e regressão Cox, o único pacote comercial que fornece informação completa com máxima probabilidade de dados ausentes é Mplus.
Uma outra limitação potencial ao usar informação completa com máxima probabilidade é que pode haver uma hipótese subjacente de normalidade multivariada. No entanto, violações da suposição de normalidade multivariada podem não ser tão importantes assim pode ser aceitável incluir variáveis binárias independentes na análise .
Incluímos no arquivo Additional file 1 um programa (SAS) que produz um conjunto completo de dados de brinquedo incluindo várias análises diferentes destes dados. As tabelas 1 e 2 mostram a saída e como diferentes métodos que lidam com dados ausentes produzem resultados diferentes.
Análise de regressão de valores de painel
Dados de painel geralmente estão contidos em um arquivo de dados chamado amplo onde a primeira linha contém os nomes das variáveis, e as linhas subsequentes (uma para cada paciente) contêm os valores correspondentes. O resultado é representado por diferentes variáveis – uma para cada medida planejada e cronometrada do resultado. Para analisar os dados, deve-se converter o arquivo em um arquivo chamado arquivo longo com um registro por medição do resultado planejado, incluindo o valor do resultado, o tempo de medição e uma cópia de todos os outros valores de variáveis excluindo os da variável do resultado. Para manter as correlações intra-paciente entre as medições de resultados cronometrados, é prática comum realizar uma múltipla imputação do arquivo de dados em sua ampla forma, seguida por uma análise do arquivo resultante após ter sido convertido para sua forma longa. O processo misto (SAS 9.4) pode ser usado para a análise de valores de resultados contínuos e o processo glimmix (SAS 9.4) para outros tipos de resultados. Como esses procedimentos aplicam o método de máxima verosimilhança direta nos dados do resultado, mas ignoram casos com valores covariados ausentes, os procedimentos podem ser usados diretamente quando apenas valores de variáveis dependentes estão ausentes, e não há boas variáveis auxiliares disponíveis. Caso contrário, o proc. misto ou proc. glimmix (o que for apropriado) deve ser usado após uma múltipla imputação. Claramente, uma abordagem correspondente pode ser possível usando outros pacotes estatísticos.
Análises de sensibilidade
Análises de sensibilidade podem ser definidas como um conjunto de análises onde os dados são tratados de uma forma diferente em comparação com a análise primária. As análises de sensibilidade podem mostrar como suposições, diferentes daquelas feitas na análise primária influenciam os resultados obtidos . A análise de sensibilidade deve ser predefinida e descrita no plano de análise estatística, mas análises de sensibilidade pós-hoc adicionais podem ser justificadas e válidas. Quando a influência potencial dos valores em falta não estiver clara, recomendamos as seguintes análises de sensibilidade:
-
Já descrevemos o uso de análises de sensibilidade dos melhores e piores casos para mostrar o intervalo de incerteza devido à falta de dados (veja Avaliação para saber se os métodos devem ser usados para lidar com dados em falta). Nossa descrição anterior da melhor e pior análise de sensibilidade ao pior e melhor caso estava relacionada a dados ausentes sobre uma variável dicotômica ou dependente contínua, mas essas análises de sensibilidade também podem ser usadas quando faltam dados sobre variáveis de estratificação, valores de base, etc. A influência potencial dos dados ausentes deve ser avaliada para cada variável separadamente, ou seja, deve haver um cenário de melhor e pior caso para cada variável (variável dependente, o indicador de resultado e as variáveis de estratificação) com dados ausentes.
-
Se for decidido que, por exemplo, múltiplas imputações devem ser usadas, então esses resultados devem ser o resultado primário do resultado dado. Cada análise de regressão primária deve sempre ser complementada por uma análise de caso observada (ou disponível) correspondente.
Quando são usados métodos de efeito misto
Utilizar um desenho de estudo multicêntrico será frequentemente necessário para recrutar um número suficiente de participantes do estudo dentro de um período de tempo razoável . Um desenho de estudo multicêntrico também fornece uma base melhor para a generalização subsequente de seus resultados. Foi demonstrado que os métodos de análise mais comumente usados em estudos clínicos randomizados funcionam bem com um pequeno número de centros (analisando resultados dependentes de binários) . Com um número relativamente grande de centros (50 ou mais), muitas vezes é ideal usar ‘centro’ como efeito aleatório e usar métodos de análise de efeitos mistos. Muitas vezes também será válido utilizar métodos de análise de efeitos mistos ao analisar dados longitudinais . Em algumas circunstâncias pode ser válido incluir a covariação de ‘efeito aleatório’ (por exemplo ‘centro’) como uma covariação de efeito fixo durante a etapa de imputação e depois usar a análise de modelo misto ou equações de estimação generalizada (GEE) durante a etapa de análise . Contudo, a aplicação de um modelo de efeitos mistos (com, por exemplo, ‘centro’ como um efeito aleatório) implica que a estrutura multicamadas dos dados deve ser levada em consideração ao modelar a imputação múltipla. Agora, o software comercial não está directamente disponível para o fazer. No entanto, pode-se utilizar o pacote REALCOME que pode ser interfaceado com o STATA . A interface exporta os dados com valores em falta do STATA para o REALCOM onde a imputação é feita levando em conta a natureza multinível dos dados e usando um método MCMC que inclui variáveis contínuas e usando um modelo normal latente também permite um tratamento adequado de dados discretos . Os conjuntos de dados imputados podem então ser analisados utilizando o comando STATA ‘mi estimate:’ que pode ser combinado com a declaração ‘mixed’ (para um resultado contínuo) ou a declaração ‘meqrlogit’ para um resultado binário ou ordinal em STATA . Na análise dos dados do painel, no entanto, pode-se facilmente deparar com uma situação em que os dados incluem três ou mais níveis, por exemplo, medições dentro do mesmo paciente (nível-1), pacientes dentro dos centros (nível-2), e centros (nível-3) . Para não se envolver com um modelo bastante complicado que pode levar à falta de convergência ou a erros padrões instáveis e para os quais não existe software comercial disponível, recomendamos que se trate o efeito centro como fixo (directamente ou após a fusão de pequenos centros em um ou mais centros de tamanho apropriado, utilizando um procedimento que deve ser prescrito no plano de análise estatística) ou se exclua o centro como covariável. Se a randomização tiver sido estratificada por centro, esta última abordagem conduzirá a um viés ascendente dos erros padrão resultando num procedimento de teste um pouco conservador .