Introductory Business Statistics

Considerar o seguinte conjunto de dados.
4; 5; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 10

Este conjunto de dados pode ser representado pelo seguinte histograma. Cada intervalo tem largura um, e cada valor está localizado no meio de um intervalo.

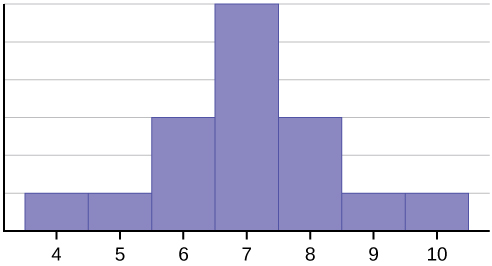
O histograma exibe uma distribuição simétrica dos dados. Uma distribuição é simétrica se uma linha vertical puder ser desenhada em algum ponto do histograma de tal forma que a forma à esquerda e à direita da linha vertical sejam imagens espelhadas uma da outra. A média, a mediana e o modo são cada sete para estes dados. Em uma distribuição perfeitamente simétrica, a média e a mediana são a mesma coisa. Este exemplo tem uma modalidade (unimodal), e a modalidade é a mesma que a média e a mediana. Em uma distribuição simétrica que tem dois modos (bimodal), os dois modos seriam diferentes da média e da mediana.

O histograma para os dados: 4566677778 não é simétrico. O lado direito parece “cortado” em comparação com o lado esquerdo. Uma distribuição deste tipo é chamada de inclinada para a esquerda porque é puxada para a esquerda. Podemos medir formalmente o enviesamento de uma distribuição tal como podemos medir matematicamente o peso central dos dados ou a sua “espeadidade” geral. A fórmula matemática para o enviesado é: . Quanto maior o desvio de zero indica um maior grau de enviesamento. Se o enviesamento for negativo, então a distribuição é enviesada para a esquerda como em (Figura). Uma medida positiva de enviesamento indica enviesamento para a direita, como em (Figura).

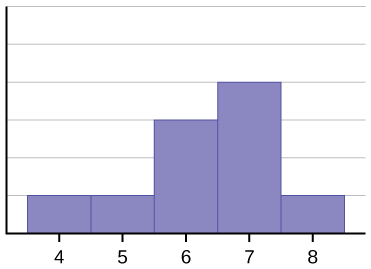
A média é 6,3, a mediana é 6,5, e o modo é sete. Note que a média é menor que a mediana, e ambas são menores que o modo. A média e a mediana refletem ambas a inclinação, mas a média reflete mais assim.

O histograma para os dados: 67777888910, também não é simétrico. É enviesado para a direita.

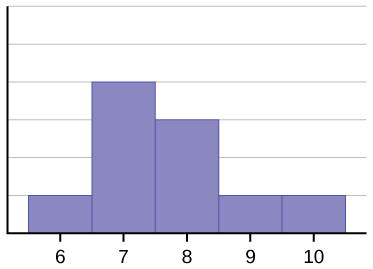
A média é 7,7, a mediana é 7,5, e o modo é sete. Das três estatísticas, a média é a maior, enquanto a modalidade é a menor. Novamente, a média reflete a inclinação máxima.

Para resumir, geralmente se a distribuição dos dados é inclinada para a esquerda, a média é menor do que a mediana, que muitas vezes é menor do que a moda. Se a distribuição dos dados for enviesada para a direita, a moda é frequentemente menor que a mediana, que é menor que a média.

Como veremos em breve, a variância, existem fórmulas matemáticas que nos dão medidas precisas destas características da distribuição dos dados. Olhando novamente para a fórmula de skewness vemos que esta é uma relação entre a média dos dados e as observações individuais em cubo.

onde é o desvio padrão da amostra dos dados, , e é a média aritmética e é o tamanho da amostra.

Formalmente a média aritmética é conhecida como o primeiro momento da distribuição. O segundo momento que veremos é a variância, e a obliquidade é o terceiro momento. A variância mede as diferenças quadráticas dos dados a partir da média e a assimetria mede as diferenças em cubos dos dados a partir da média. Enquanto uma variância nunca pode ser um número negativo, a medida da assimetria pode e é assim que determinamos se os dados são inclinados da direita para a esquerda. O enviesamento para uma distribuição normal é zero, e qualquer dado simétrico deve ter um enviesamento próximo de zero. Valores negativos para o enviesado indicam dados que são enviesados para a esquerda e valores positivos para o enviesado indicam dados que são enviesados para a direita. Por enviesado para a esquerda, queremos dizer que a cauda esquerda é longa em relação à cauda direita. Da mesma forma, a direita enviesada significa que a cauda direita é longa em relação à cauda esquerda. O enviesado caracteriza o grau de assimetria de uma distribuição em torno da sua média. Enquanto a média e o desvio padrão são quantidades dimensionais (é por isso que vamos tomar a raiz quadrada da variância ) ou seja, ter as mesmas unidades que as quantidades medidas , a assimetria é convencionalmente definida de tal forma a torná-la não dimensional. É um número puro que caracteriza apenas a forma da distribuição. Um valor positivo de obliquidade significa uma distribuição com uma cauda assimétrica estendendo-se para mais X positivo e um valor negativo significa uma distribuição cuja cauda se estende para mais X negativo. Uma medida zero de obliquidade indicará uma distribuição simétrica.

A obliquidade e simetria tornam-se importantes quando discutimos distribuições de probabilidade em capítulos posteriores.