Posto em 29 de Novembro de 2018 por Maximilian Siebert
Heterogeneidade não é algo a temer, apenas significa que há variabilidade nos seus dados. Assim, se se reúne diferentes estudos para analisá-los ou fazer uma meta-análise, é claro que haverá diferenças encontradas. O oposto de heterogeneidade é a homogeneidade, o que significa que todos os estudos mostram o mesmo efeito.
É importante notar que existem diferentes tipos de heterogeneidade:
- Clínica: Diferenças nos participantes, intervenções ou resultados
- Metodológico: Diferenças no desenho do estudo, risco de viés
- Estatística: Variação nos efeitos ou resultados da intervenção
Estamos interessados nessas diferenças porque elas podem indicar que nossa intervenção pode não estar funcionando da mesma maneira toda vez que é utilizada. Ao investigar essas diferenças, você pode alcançar um entendimento muito maior sobre quais fatores influenciam a intervenção, e que resultado você pode esperar da próxima vez que a intervenção for implementada.
Embora a heterogeneidade clínica e metodológica seja importante, este blog estará focando na heterogeneidade estatística.
Como identificar e medir a heterogeneidade
Teste ocular
Na sua parcela florestal, dê uma olhada em intervalos de confiança sobrepostos, ao invés de saber de que lado estão suas estimativas de efeitos. Se os resultados estão em ambos os lados da linha de nenhum efeito pode não afetar sua avaliação sobre se a heterogeneidade está presente, mas pode influenciar sua avaliação sobre se a heterogeneidade é importante.
Com isso em mente, dê uma olhada no gráfico abaixo e decida qual parcela é mais homogênea.
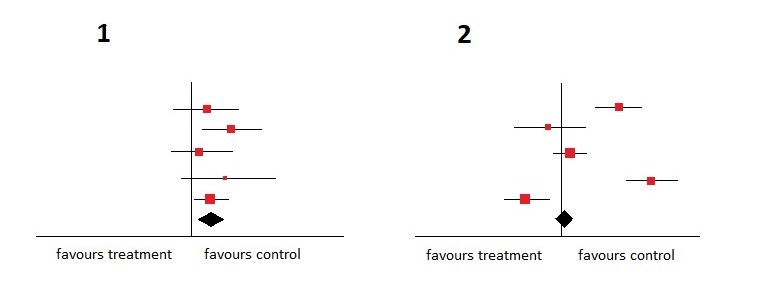
De fato, quanto mais homogênea for a parcela número 1 . Os intervalos de confiança são todos sobrepostos e, além disso, todos os estudos favorecem a intervenção de controle.
Para as pessoas que gostam de medir as coisas em vez de apenas olhar para elas, não se preocupe, ainda existem alguns métodos estatísticos para ajudá-lo a apreender o conceito de heterogeneidade.
Chi-squared (χ²) test
Este teste assume a hipótese nula de que todos os estudos são homogêneos, ou que cada estudo está medindo um efeito idêntico, e nos dá um p-valor para testar esta hipótese. Se o valor de p do teste for baixo podemos rejeitar a hipótese e a heterogeneidade está presente.
Porque o teste muitas vezes não é suficientemente sensível e a exclusão errada da heterogeneidade acontece rapidamente, muitos cientistas usam um valor de p de < 0,1 ao invés de < 0,05 como o corte.
I²
Este teste foi desenvolvido pelo Professor Julian Higgins e tem uma teoria para medir a extensão da heterogeneidade ao invés de afirmar se ela está presente ou não.
Limiares para a interpretação de I² podem ser enganosos, já que a importância da inconsistência depende de vários fatores. Um guia aproximado para interpretação é o seguinte:
- 0% a 40%: pode não ser importante
- 30% a 60%: heterogeneidade moderada
- 50% a 90%: heterogeneidade substancial
- 75% a 100%: heterogeneidade considerável
Para entender a teoria acima, dê uma olhada no exemplo a seguir.
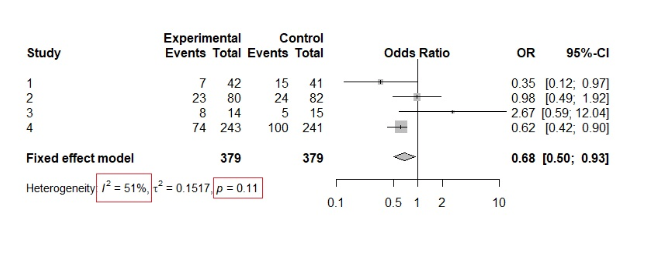
Vemos que o p-valor do teste do qui-quadrado é 0,11, confirmando a hipótese nula e sugerindo assim homogeneidade. No entanto, olhando para as intervenções, já podemos ver alguma heterogeneidade nos resultados. Além disso, o valor I² é 51% sugerindo heterogeneidade moderada a substancial.
Este é um bom exemplo de como o teste χ² pode ser enganador quando existem apenas alguns estudos na meta-análise.
Como lidar com a heterogeneidade?
Após ter detectado variabilidade nos seus resultados, é necessário lidar com ela. Aqui estão alguns passos sobre como você pode tratar este problema:
- Verifique os seus dados para erros – Volte atrás e veja se você talvez tenha digitado algo errado
- Não faça uma meta-análise se a heterogeneidade for muito alta – Nem toda revisão sistemática precisa de uma meta-análise
- Explore a heterogeneidade – Isto pode ser feito por análise de subgrupos ou meta-análiseregressão
- Executar uma meta-análise de efeitos aleatórios – Tenha em mente que esta abordagem é para heterogeneidade que não pode ser explicada porque é devido ao acaso
- Mudar as medidas de efeito – Digamos que você usa a Diferença de Risco e tem alta heterogeneidade, então experimente o Risk Ratio ou Odds Ratio
(1) Fletcher, J. O que é heterogeneidade e o que é importante? BMJ 2007; 334 :94
(2) Deeks JJ, Higgins JPT, Altman DG (editores). Capítulo 9: Análise de dados e realização de meta-análises. In: Higgins JPT, Green S (editores). Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 . A Colaboração Cochrane, 2011. Disponível em www.cochrane-handbook.org.
(3) https://www.mathsisfun.com/data/chi-square-test.html