Apenas como bolo você poderia ter 2 peças pequenas ou 1 peça duas vezes maior e é a mesma quantidade. Portanto, muitas frações são equivalentes, como 2/5 e 4/10.


Any Number Can Be Written As a Fraction
Escrever qualquer número inteiro sobre 1 para torná-lo uma fração, uma vez que o número total de partes em qualquer todo indiviso é um.
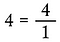
Frações Multiplicadas Retas
Frações Multiplicadas é fácil, basta multiplicar diretamente.
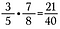
Nota: Os números mistos devem ser convertidos em frações impróprias primeiro, leia para saber mais sobre isto.
Multiply By Any Form of One Anytime
O número 1 é chamado de identidade multiplicativa porque podemos multiplicá-lo por qualquer número e o número permanece o mesmo. Isto é importante para frações porque muitas vezes precisamos alterar a aparência de uma fração sem realmente alterar seu valor.
Por exemplo, eu posso alterar 1/3 para a fração equivalente a 3/9 multiplicando por 3/3.
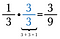
Adicionar e Subtrair Partes de Tamanho Igual
Ao adicionar e subtrair frações os denominadores devem ser os mesmos. Isso faz sentido. Se quisermos combinar ou retirar partes, devemos estar a falar das mesmas partes de tamanho, caso contrário, ficaria confuso.
>
Então o que fazer se as suas fracções não tiverem os mesmos tamanhos?
>
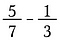
>
>
Multiplicar por uma forma de um para mudar os denominadores para um tamanho comum. Essencialmente, estamos dividindo as frações em peças de menor tamanho até que elas tenham o mesmo tamanho. Isto é chamado de encontrar um denominador comum.
Na verdade, qualquer denominador comum serve, mas as pessoas preferem encontrar o menor. Neste caso, o menor número, tanto o 7 como o 3, são 21 sem o restante. Então multiplique a primeira fração por 3/3 e a segunda por 7/7,
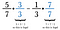
Se você não consegue pensar no denominador menos comum, você pode sempre multiplicar cada fração pela denominação oposta. Por vezes, como neste caso, isso acaba por ser o denominador menos comum. Se não for, basta reduzir a sua resposta no final.
Após os denominadores serem correspondentes, subtraia os numeradores para obter 8/21.
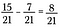
Esta funciona como seria de esperar. Pictoricamente, comece com 15 peças de 21 total.

Remover a coloração de 7 dos 15 blocos azuis.

>
Que deixa 8/21 como esperado.
Mudar primeiro os números mistos
Um número misto é a combinação de um número inteiro e uma fração.
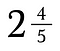
Números mistos não jogam bem com outras fracções. É uma boa idéia convertê-los em frações impróprias primeiro.
Nota: Uma fração imprópria é uma fração cujo numerador é maior do que o seu denominador, portanto tendo um valor maior do que um.
Convertendo um Número Misto é Realmente Adição
Para converter 2 e 4/5 em uma fração imprópria adicione 2 + 4/5.
Passo 1: Comece reescrevendo 2 como 2/1.
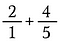
Passo 2: Multiplique 2/1 por 5/5 para fazer uma fração equivalente a 10/5, que tem o denominador comum desejado de 5.
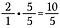
Passo 3: Adicionar 10/5 + 4/5.
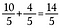
>
>
Nosso resultado é a fração imprópria equivalente 14/5.
>
Para converter de volta para um número misto realize a divisão. Por exemplo, 5 vai em 14 duas vezes (desde 5 x 2 = 10) com 4 peças restantes.
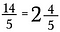
Fracções Comparadas Usando o Produto Cruzado
Suponhamos que queríamos determinar qual é maior: 5/12 ou 6/13.
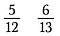
Passo um: Multiplique uma diagonal e escreva o produto acima do numerador.
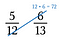
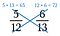
Passo dois: Multiplique a outra diagonal e escreva seu produto acima do numerador.
>
>
>
>
Três passos: Comparar os produtos. O lado com o produto maior é a fração maior. Portanto, neste caso, 5/12 é inferior a 6/13.
>
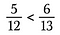
Podemos determinar se as frações são iguais usando produtos cruzados também.
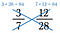
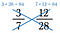
O produto cruzado de 3/7 e 12/28 são ambos 84, portanto 3/7 = 12/28.
Cancelar Tudo o que Dividir para Um
A melhor coisa sobre frações é que você pode encontrar muitas oportunidades para cancelar. O que as torna rápidas e fáceis de gerenciar.
Ponha que eu tenha a fração 8/10. Ambos 8 e 10 podem ser reescritos com 2 como fator.
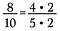
Porque 2/2 = 1, posso cancelar os 2 deixando 4/5 como a fração reduzida.
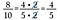
Utiliza esta estratégia para facilitar também a multiplicação das fracções.
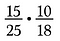
>
Begin, reescrevendo cada número em factores.
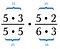
>
>
Cancelar quaisquer pares de números que se dividem em 1. Por exemplo, 5/5 = 1,
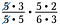
Eu tenho outro par de 5 assim como um par de 3 que se divide também em 1.
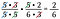
Oops! Eu poderia ter reescrito 6 como 2 x 3 e cancelado um par de 2’s. Tudo bem se você perder um fator, continue até conseguir todos.
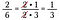
Had multiplicado 15/25 vezes 10/18 diretamente teria sido muito aritmético, usando o cancelamento eu pre-reduzo as frações e simplifico a multiplicação.
Utilizar multiplicação para dividir frações
O conceito de dividir frações é fácil com exemplos simples como:

Existem duas metades em um todo, portanto existem 10 metades em 5 atacados.
Mas o conceito torna-se complicado com fracções mais complicadas.
Para resolver este problema vamos utilizar dois factos:
- Podemos multiplicar por qualquer forma de um (i.e qualquer coisa sobre si mesmo)
- Multiplicando pelo recíproco de 3/2, que é 2/3, resulta em 1 via cancelamento
Passo um: Comece multiplicando pelo recíproco sobre si mesmo.
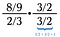
Agora temos dois problemas menores para resolver (azul e verde).
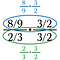
Step dois: Cancelar qualquer coisa que se divida em 1 na fracção inferior (verde). Isto deve sempre resultar em 1.

Agora ficamos com o problema superior para resolver.
>
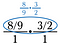 >
>>>
>
>
>
Step três: Use o cancelamento para pré-reduzir a fração. Depois de fazer estas reduções, multiplique para obter 4/3.

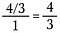
>
Shortcut
Esta é a mecânica da mão longa de “virar e multiplicar”.”
Podemos saltar a multiplicação pelo recíproco no fundo já que sempre cancela a 1. Portanto tudo que você precisa fazer é multiplicar o numerador pelo recíproco do denominador.

Bonus: Teoria, caso você esteja interessado…
Grande pergunta! Para generalizar, faça duas frações usando as letras a, b, c e d para representar quatro números diferentes.
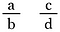
Multiplicar ambas as frações por b-d (isto nos permitirá cancelar os denominadores).
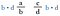
>
Agora cancele os b’s à esquerda e os d’s à direita, pois eles se dividem em 1. Não temos mais frações, apenas os produtos d-a e c-b.
>
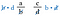
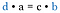
>
Veja as frações originais. Estes são os mesmos produtos como se tivéssemos multiplicado as diagonais. Portanto, o atalho é comparar o produto cruzado.
❤ STAY CONNECTED ❤
Estar actualizado com tudo o que os Math Hacks fazem até!