Recentemente, um colega meu fez-me algumas perguntas como “porque é que temos tantas funções de activação?”, “porque é que uma funciona melhor que a outra?”, “como é que sabemos qual usar?”, “é matemática hardcore?” e assim por diante. Então eu pensei, porque não escrever um artigo sobre isso para aqueles que estão familiarizados com rede neural apenas em um nível básico e está, portanto, se perguntando sobre funções de ativação e sua “por que – como – matemática!”.
NOTE: Este artigo assume que você tem um conhecimento básico de um “neurônio” artificial. Eu recomendaria ler o básico sobre redes neurais antes de ler este artigo para melhor entendimento.
Funções de ativação
Então o que um neurônio artificial faz? Simplificando, ele calcula uma “soma ponderada” de sua entrada, adiciona um viés e então decide se deve ser “despedido” ou não ( sim, uma função de ativação faz isso, mas vamos com o fluxo por um momento ).
Pondera um neurônio.
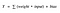
>
Agora, o valor de Y pode ser qualquer coisa variando de -inf a +inf. O neurônio realmente não sabe os limites do valor. Então como decidimos se o neurônio deve ou não disparar ( por que este padrão de disparo? Porque aprendemos com a biologia que é assim que o cérebro funciona e o cérebro é um testemunho funcional de um sistema impressionante e inteligente ).
Decidimos adicionar “funções de ativação” para este propósito. Para verificar o valor Y produzido por um neurônio e decidir se as conexões externas devem considerar este neurônio como “demitido” ou não. Ou melhor, digamos – “ativado” ou não.
Função de passo
A primeira coisa que nos vem à mente é que tal uma função de ativação baseada em limite? Se o valor de Y estiver acima de um certo valor, declare-a activada. Se for menor que o limite, então diga que não é. Hmm ótimo. Isto poderia funcionar!
Função de ativação A = “ativada” se Y > limiar, senão não
Alternativamente, A = 1 se y> limiar, 0 senão Bem, o que acabamos de fazer é uma “função de passo”, veja a figura abaixo.
>
Saída de Its é 1 ( ativada) quando o valor > 0 (limiar) e sai um 0 ( não ativado) caso contrário.
Grande. Então isto faz uma função de ativação para um neurônio. Sem confusões. No entanto, há certos inconvenientes com isto. Para entender melhor, pense no seguinte.
Suponha que você está criando um classificador binário. Algo que deve dizer “sim” ou “não” ( ativar ou não ativar ). Uma função Step poderia fazer isso por você! É exatamente isso que ela faz, diga um 1 ou 0. Agora, pense no caso de uso em que você gostaria que vários desses neurônios fossem conectados para trazer mais classes. Classe 1, classe 2, classe 3, etc. O que acontecerá se mais de 1 neurônio for “ativado”. Todos os neurônios sairão um 1 (da função passo a passo). Agora o que você decidiria? Qual classe é ela? Hmm difícil, complicada.
Você quereria que a rede ativasse apenas 1 neurônio e outros deveriam ser 0 ( só então você poderia dizer que classificou corretamente/identificou a classe ). Ah! Isto é mais difícil de treinar e convergir desta forma. Teria sido melhor se a ativação não fosse binária e em vez disso diria “50% ativada” ou “20% ativada” e assim por diante. E então se mais de 1 neurônio ativa, você poderia encontrar qual neurônio tem a “maior ativação” e assim por diante ( melhor que max, um softmax, mas vamos deixar isso por enquanto ).
Neste caso também, se mais de 1 neurônio diz “100% ativado”, o problema ainda persiste.Eu sei! Mas…como existem valores intermediários de ativação para o output, o aprendizado pode ser mais suave e fácil ( menos perspicaz ) e as chances de mais de 1 neurônio estar 100% ativado é menor quando comparado à função de passo durante o treinamento ( também dependendo do que você está treinando e dos dados ).
Ok, então queremos algo que nos dê valores intermediários ( analógicos ) de ativação ao invés de dizer “ativado” ou não ( binário ).
A primeira coisa que nos vem à cabeça seria função linear.
Função linear
A = cx Uma função de linha reta onde a ativação é proporcional à entrada ( que é a soma ponderada do neurônio ). Desta forma, ele dá uma gama de ativações, portanto não é ativação binária. Podemos definitivamente conectar alguns neurônios juntos e se mais de 1 disparo, podemos pegar o máximo ( ou softmax) e decidir com base nisso. Então isso também está bem. Então qual é o problema com isto?
Se você está familiarizado com a descida de gradiente para treinamento, você notaria que para esta função, derivada é uma constante.
A = cx, derivada com respeito a x é c. Isso significa que o gradiente não tem relação com X. É um gradiente constante e a descida vai ser em gradiente constante. Se houver um erro na previsão, as alterações feitas pela propagação de retorno são constantes e não dependem da mudança no delta de entrada(x) !!!
Isso não é tão bom assim! ( nem sempre, mas tenha paciência comigo ). Há outro problema também. Pense em camadas conectadas. Cada camada é ativada por uma função linear. Essa ativação por sua vez vai para o próximo nível como entrada e a segunda camada calcula a soma ponderada sobre essa entrada e ela, por sua vez, dispara baseada em outra função de ativação linear.
Não importa quantas camadas temos, se todas são lineares por natureza, a função de ativação final da última camada não é nada além de uma função linear da entrada da primeira camada! Pausa um pouco e pense nisso.
Isso significa que essas duas camadas ( ou N camadas ) podem ser substituídas por uma única camada. Ah! Acabamos de perder a capacidade de empilhar camadas desta forma. Não importa como empilhamos, toda a rede ainda é equivalente a uma única camada com ativação linear ( uma combinação de funções lineares de forma linear ainda é outra função linear ).
Prossigamos, vamos?
Função Sigmóide
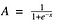
>
Bem, isto parece suave e “função passo a passo”. Quais são os benefícios disto? Pense nisso por um momento. Em primeiro lugar, é de natureza não linear. Combinações desta função também são não-lineares! Ótimo. Agora podemos empilhar camadas. E as ativações não binárias? Sim, isso também! Vai dar uma activação analógica ao contrário da função de passo. Tem um gradiente suave também.
E se você notar, entre os valores X -2 a 2, os valores Y são muito íngremes. O que significa que qualquer pequena alteração nos valores de X naquela região fará com que os valores de Y mudem significativamente. Ah, isso significa que essa função tem a tendência de trazer os valores de Y para ambos os extremos da curva.
Parece que é bom para um classificador considerando sua propriedade? Sim, de facto é. Ela tende a trazer as ativações para cada lado da curva (acima x = 2 e abaixo x = -2 por exemplo). Fazendo distinções claras na previsão.
Uma outra vantagem desta função de ativação é que, ao contrário da função linear, a saída da função de ativação estará sempre no intervalo (0,1) em comparação com (-inf, inf) da função linear. Portanto, temos as nossas activações ligadas num intervalo. Nice, não vai explodir as ativações então.
Isso é ótimo. As funções Sigmoid são uma das funções de ativação mais usadas hoje em dia. Então quais são os problemas com isso?
Se você notar, em ambos os lados da função sigmóide, os valores Y tendem a responder muito menos a mudanças no X. O que isso significa? O gradiente nessa região vai ser pequeno. Isso dá origem a um problema de “gradientes em fuga”. Hmm. Então o que acontece quando as ativações chegam perto da parte “quase horizontal” da curva em ambos os lados?
Gradiente é pequeno ou desapareceu ( não pode fazer mudanças significativas por causa do valor extremamente pequeno ). A rede se recusa a aprender mais ou é drasticamente lenta ( dependendo do caso de uso e até que o gradiente /computação seja atingido pelos limites do valor do ponto flutuante ). Existem formas de contornar este problema e o sigmóide ainda é muito popular em problemas de classificação.
Função Tanh
Outra função de ativação que é usada é a função tanh.
>
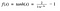
>
Hm. Isto parece muito semelhante ao sigmóide. Na verdade, é uma função sigmóide em escala!

Ok, agora isto tem características semelhantes à sigmóide que discutimos acima. É de natureza não-linear, tão grande que podemos empilhar camadas! Está vinculado ao intervalo (-1, 1) para que não haja preocupações de ativações que explodam. Um ponto a mencionar é que o gradiente é mais forte para o tanh do que o sigmóide (os derivados são mais íngremes). Decidir entre o sigmóide ou o tanh vai depender da sua exigência de força de gradiente. Tal como o sigmóide, tanh também tem o problema do gradiente de fuga.
Tanh também é uma função de ativação muito popular e amplamente utilizada.
ReLu
Later, vem a função ReLu,
A(x) = max(0,x) A função ReLu é como mostrado acima. Ela dá uma saída x se x for positivo e 0 caso contrário.
No primeiro olhar isto pareceria ter os mesmos problemas de função linear, pois ela é linear em eixo positivo. Primeiro de tudo, ReLu é não linear por natureza. E as combinações de ReLu também são não lineares! ( na verdade, é um bom aproximador. Qualquer função pode ser aproximada com combinações de ReLu). Ótimo, então isso significa que podemos empilhar camadas. No entanto, não está vinculado. O intervalo de ReLu é [0, inf). Isto significa que ele pode explodir a ativação.
Outro ponto que eu gostaria de discutir aqui é a sparsity da ativação. Imagine uma grande rede neural com muitos neurônios. Usar um sigmóide ou tanh fará com que quase todos os neurônios disparem de forma análoga ( lembra-se? ). Isso significa que quase todas as ativações serão processadas para descrever a saída de uma rede. Em outras palavras, a ativação é densa. Isto é caro. O ideal seria que alguns neurônios da rede não fossem ativados e assim tornar as ativações esparsas e eficientes.
ReLu nos dá este benefício. Imagine uma rede com pesos inicializados aleatórios ( ou normalizados ) e quase 50% da rede produz ativação 0 por causa da característica de ReLu ( output 0 para valores negativos de x ). Isto significa que menos neurônios estão disparando ( ativação esparsa ) e a rede é mais leve. Woah, legal! ReLu parece ser fantástico! Sim é, mas nada é impecável… Nem mesmo ReLu.
Por causa da linha horizontal em ReLu( para X negativo ), o gradiente pode ir para 0. Para ativações naquela região de ReLu, o gradiente será 0 por causa do qual os pesos não serão ajustados durante a descida. Isso significa que aqueles neurônios que entram nesse estado vão parar de responder às variações de erro/entrada ( simplesmente porque o gradiente é 0, nada muda ). Isto é chamado de problema ReLu moribundo. Este problema pode causar a morte de vários neurônios e não responder, tornando uma parte substancial da rede passiva. Existem variações no ReLu para mitigar este problema simplesmente tornando a linha horizontal em componente não-horizontal . por exemplo y = 0,01x para x<0 fará dela uma linha ligeiramente inclinada ao invés da linha horizontal. Isto é um vazamento em ReLu. Existem outras variações também. A idéia principal é deixar o gradiente não ser zero e eventualmente recuperar durante o treinamento.
ReLu é menos computacionalmente caro que Tanh e sigmóide porque envolve operações matemáticas mais simples. Esse é um bom ponto a considerar quando estamos desenhando redes neurais profundas.
Ok, agora qual delas usamos?
Agora, quais funções de ativação usar. Isso significa que usamos apenas ReLu para tudo o que fazemos? Ou sigmoid ou tanh? Bem, sim e não. Quando você sabe que a função que você está tentando aproximar tem certas características, você pode escolher uma função de ativação que irá aproximar a função mais rápido levando a um processo de treinamento mais rápido. Por exemplo, um sigmoid funciona bem para um classificador ( veja o gráfico do sigmoid, ele não mostra as propriedades de um classificador ideal? ) porque aproximar uma função de classificador como combinações de sigmoid é mais fácil do que talvez ReLu, por exemplo. O que levará a um processo de treinamento e convergência mais rápidos. Você pode usar suas próprias funções personalizadas também!… Se você não conhece a natureza da função que você está tentando aprender, então talvez eu sugira começar com ReLu, e depois trabalhar de trás para frente. ReLu funciona na maioria das vezes como um aproximador geral!
Neste artigo, eu tentei descrever algumas funções de ativação usadas comumente. Existem outras funções de ativação também, mas a idéia geral permanece a mesma. A pesquisa para melhores funções de ativação ainda está em andamento. Espero que você tenha tido a idéia por trás da função de ativação, porque elas são usadas e como decidimos qual delas usar.