As equações de Lotka-Volterra descrevem um modelo ecológico predador-presa (ou parasita-anfitrião) que assume isso, para um conjunto de constantes positivas fixas 
(a taxa de crescimento das presas), 
(a taxa à qual os predadores destroem as presas), 
(a taxa de mortalidade dos predadores), e 
(a taxa à qual os predadores aumentam ao consumirem presas), as seguintes condições se mantêm.
1. Uma população de presas 
aumenta a uma taxa 
(proporcional ao número de presas) mas é simultaneamente destruída por predadores a uma taxa 
(proporcional ao produto do número de presas e predadores).
2. Uma população de predadores 
diminui a uma taxa 
(proporcional ao número de predadores), mas aumenta a uma taxa 
(novamente proporcional ao produto do número de presas e predadores).
>
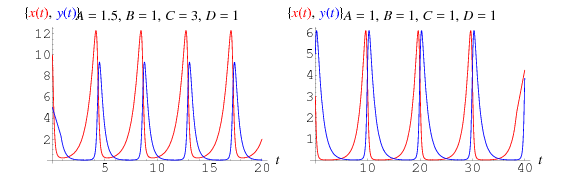
Esta dá as equações diferenciais acopladas
 |
 |
 |
(1)
|
 |
 |
(2)
|
soluções das quais estão plotadas acima, onde as presas são mostradas em vermelho, e os predadores em azul. Neste tipo de modelo, a curva da presa lidera sempre a curva do predador.
Os pontos críticos ocorrem quando 
, so
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
O único ponto estacionário está, portanto, localizado em 
.