Introdução
Esta página revisa a equação de continuidade, que obriga à conservação da massa em uma análise Euleriana. Isto não é estritamente uma descrição do comportamento material, mas a equação resultante é muitas vezes usada como uma identidade para manipular de forma criativa os modelos constitutivos que descrevem o comportamento material. Portanto, vale a pena rever. Ela também é central para a análise do fluxo de fluidos porque as análises clássicas de fluidos não podem ser Lagrangianas já que as posições de todas as partículas de fluidos em \(t = 0\) são desconhecidas.
Conservação de Massa
A equação de continuidade reflete o fato de que a massa é conservada em qualquer análise mecânica não-nuclear contínua. A equação é desenvolvida pela soma da taxa na qual a massa está fluindo para dentro e para fora de um volume de controle, e estabelecendo o fluxo líquido igual à taxa de variação de massa dentro dela. Isto é demonstrado na figura em baixo.
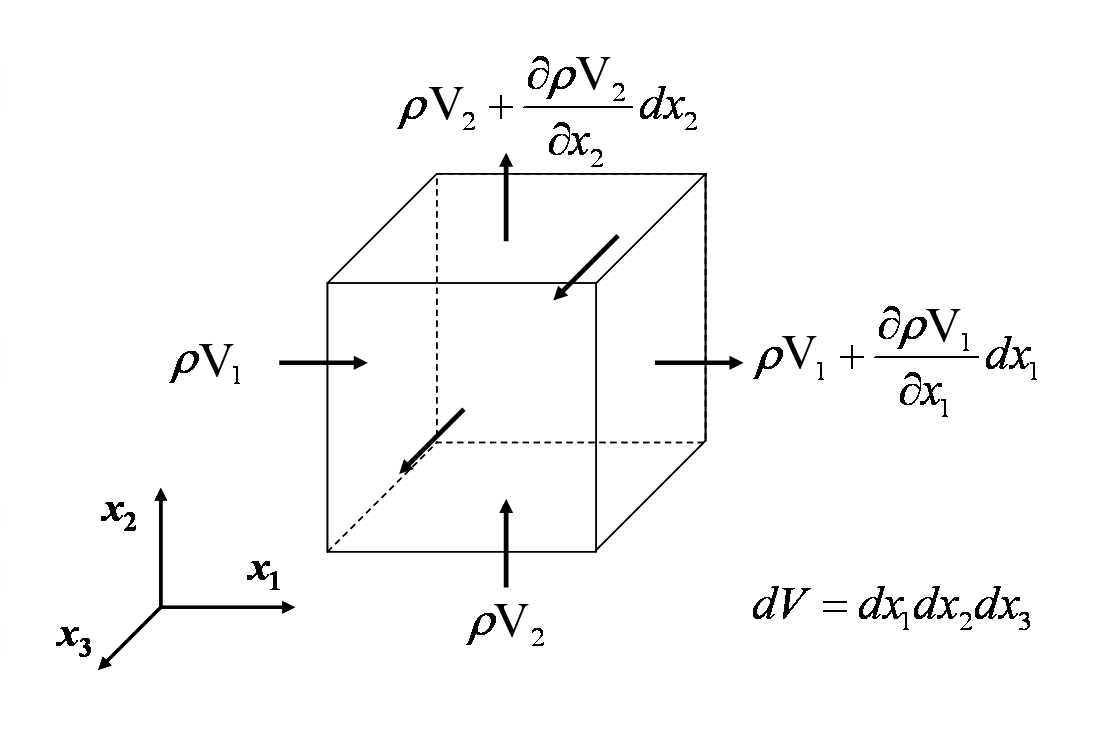
Equadrando todas as taxas de fluxo de massa para dentro e para fora do controlvolume diferencial dá
Cancelando termos e dividindo por \(dx_1 dx_2 dx_3\) dá
e o rearranjo dá
>Esta pode ser escrita concisamente como

Pontos Importantes
Estas são as finais, completas, e as formas mais gerais da sequenciação contínua que impõe a conservação da massa. Ela se aplica a todos os materiais, não apenas aos fluidos. Portanto, também se aplica aos sólidos. Note que é uma equação escalar única e é Euleriana por natureza porque os gradientterms são parciais x_i, não X_i parciais).
Uma pessoa poderia se perguntar se existe uma contraparte Lagrangiana para a forma Euleriana disto. E há. Isto diz simplesmente que o pedaço de massa diferencial no estado deformado deve ser igual ao seu valor original (rho_o dV_o) no estado não-formado.
O segundo caso especial é o da incompressibilidade, ou seja \Neste caso, a derivada em relação ao tempo é zero e a derivada em relação ao tempo pode ser excluída da equação, deixando apenas 75567556.
Note que isto nada mais é do que \\(\texto{tr}({\bf D}) = 0\) para o caso de materiais incompressíveis.

Material Derivado
Vale a pena salientar o seguinte porque permite separar o vector de densidade e velocidade. O primeiro passo é aplicar a regra do produto ao termo de divergência na equação de continuidade.
E depois repare que o (D rho parcial sobre D t) + bf v) cdot nabla rho)é apenas o material derivado da densidade,>(D rho sobre D t).
Então a equação de continuidade também pode ser escrita como
Se o material é incompressível, então o material não pode mudar, por isso (“D”) deve ser zero, deixando
e depois dividir por \rho (já que não é zero) para obter

Equação de Continuidade Exemplo
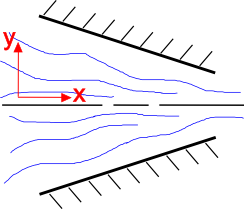
É intuitivo que o fluxo de fluido se acelera à medida que a secção transversal diminui, como se mostra à direita. A equação de continuidade explica isto. Considere um campo de fluxo em estado estacionário 2-D de um fluido incompressível. A equação de continuidade para esta situação é
Inicie olhando para o componente y do fluxo, \(v_2). A geometria do bico convergente força o componente {\i(v_2}) a fluir para cima quando o componente {\i(y {\i0}) e para baixo quando o componente {\i(y {\i0}). Assim, quando o componente (v_2) e (v_2) quando o componente (y).
O efeito líquido disto é que o bocal convergente.
Mas a equação de continuidade dita que a soma das duas derivadas parciais deve ser igual a zero. Portanto, se a segunda for menor que zero, então
E isto significa que o fluxo de fluido deve estar acelerando.