Concavo vs. convexo?

Qual é a diferença entre côncavo e convexo?

Se tivéssemos que descrever a diferença entre côncavo e convexo da forma mais geral possível, diríamos que qualquer objecto côncavo, semelhante a uma taça, é côncavo, enquanto qualquer objecto parecido com uma bola de rugby ou futebol tem uma forma convexa. Mas talvez a razão pela qual convexo e côncavo são tão comumente mal utilizados seja porque as duas palavras não são tão simples como gostaríamos que fossem.

A maior parte das fontes gramaticais insiste em como é possível usar a mnemónica para decifrar convexo e côncavo através da palavra caverna. Enquanto a noção de associar côncavo com o evento de algo “cavado” ajuda a aprender sobre características da superfície, é confuso relacionar esta idéia com assuntos envolvendo gráficos.

Para entender como côncavo e convexo são diferentes um do outro, precisamos aprender como cada termo é usado na capacidade da matemática, espelhos, lentes e, finalmente, dentro da escrita criativa. Uma vez decidido em que contexto você gostaria de usar palavras como côncavo e convexo, aprender sobre seus aspectos técnicos permitirá que você esteja mais confiante em usá-los na fala diária.

O que significa côncavo?

Concavo é usado como adjetivo ou substantivo para descrever a forma de um objeto ou superfície que é curvado para dentro ou oco para fora como uma tigela. Exemplos de côncavo em uma frase incluem,

“Ela retirou o sorvete do recipiente, deixando uma pegada côncava”,

De acordo com o The Oxford Dictionary of Word Histories, a palavra côncava deriva do inglês médio tardio. Concave e concave tornam o termo latino concavus (con- e cavus), que se traduz para ‘juntos’ e ‘ocos’ (“Concave,” 110).

Sinônimos de concave incluem:

Dentado, deprimido, côncavo, oco, recuado, encastrado e afundado.

Antónimos de côncavo incluem:

Bomba, arqueado, saliente, protuberante, saliente, protuberante.

O que significa convexo?

A palavra convexo, ou convexidade, é um adjetivo que descreve um objeto ou superfície que é arredondado ou curvo. Em relação aos objectos, a superfície média de um objecto convexo é mais larga do que o seu canto exterior. Exemplos de convexidade em uma frase incluem,

“Eu caí em hera venenosa e agora tenho saliências vermelhas e convexas em toda a minha pele”.

Sinónimos de convexidade incluem,

Arugado, dobrado, abaulado, em relevo.

Antónimos convexos incluem:

Depressão, afundamento.

Funções côncava vs convexa

Uma função convexa representa uma linha contínua em um gráfico onde o ponto médio, ou o inteiro mediano de um domínio, não excede a média do intervalo. Uma função côncava é exatamente o oposto de uma função convexa porque, para que f(x) seja côncava, f(x) deve ser negativa. Para tornar as diferenças mais claras, aqui está uma rápida análise de como os termos se comparam:

Concave para cima = convexa = convexa para baixo

Concave para baixo = convexa para cima

A diferença entre as funções côncava e convexa é mostrada mais claramente se olharmos para um gráfico. Observe como a função convexa abre para cima, enquanto a função côncava abre para baixo.

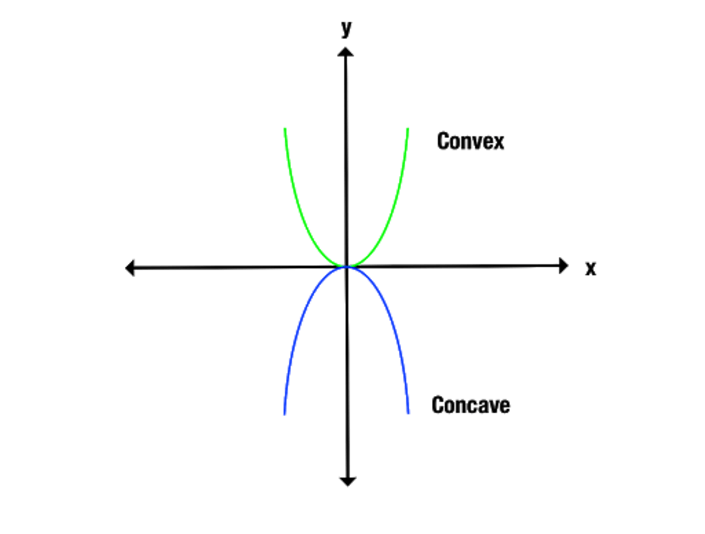
Outra forma de identificar as funções côncava e convexa é conectar pontos no gráfico ao longo do eixo x. Uma função côncava só conecta linhas abaixo do gráfico, enquanto uma função convexa só produz linhas acima do gráfico.

Podemos, adicionalmente, usar cálculo para decifrar se uma função é convexa ou côncava ou não. Se a segunda derivada de f(x) for maior que zero, então a função é convexa. Mas se a segunda derivada de f(x) for menor que zero, a função é côncava.

Polígonos convexo vs. polígonos côncavos

Não entre em pânico, mas as palavras convexo e côncavo também são usadas para geometria. As formas convexa e côncava são mais frequentemente discutidas em referência aos polígonos, que são formas com um mínimo de três lados e ângulos.

Pólígonos regulares existem com lados e ângulos iguais, mas polígonos convexos e côncavos são um pouco mais complicados. Os polígonos convexos contêm ângulos internos inferiores a 180 graus, enquanto os polígonos côncavos contêm um ou mais ângulos internos superiores a 180 graus.

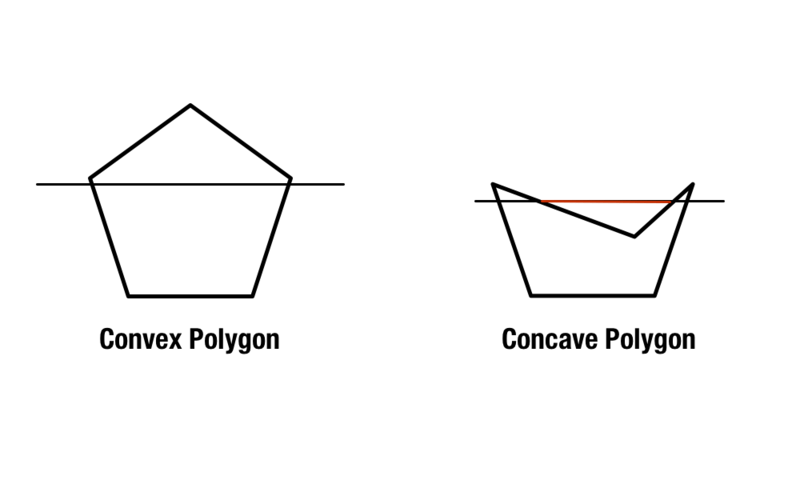
Um segundo método para identificar polígonos côncavos e convexos é desenhar duas linhas diagonais através da forma, a partir dos cantos da forma. Se cada linha existe dentro da forma, a forma é convexa. Se houver pelo menos uma linha que cruze fora da forma, ela é côncava.

Espelhos côncavos vs. convexos

As palavras côncavo e convexo são comumente usadas enquanto se discute objetos ópticos, como espelhos e lentes. Qualquer superfície convexa se projetará para fora, semelhante a uma bolha, o que dá o efeito de amplitude. Espelhos convexos são comumente encontrados dentro de garagens de estacionamento, onde os motoristas precisam de uma visão ampla em torno de cantos ou potenciais pontos cegos.

Em contraste, um espelho côncavo é curvo para dentro e produz uma reflexão ampliada que é de cabeça para baixo. Como mostra a Escola de Física da Universidade de Gales do Sul, qualquer pessoa com uma colher brilhante pode testar esta observação, olhando para o seu reflexo na colher. Na superfície côncava da colher, onde você pega sua comida, seu reflexo é distorcido de forma estreita, e você aparecerá de cabeça para baixo. Mas se você virar sua colher para o lado convexo, seu reflexo será vertical e menor.

Os reflexos variam tanto entre superfícies convexas e côncavas porque quer a superfície se curve ou não para fora ou para dentro, o espelho em si é parte de uma esfera. Como a superfície de uma esfera não é plana, a luz reflectida da sua superfície percorre distâncias diferentes antes de contactar o espelho.

Dependente da área da superfície em que a luz faz contacto, um raio de luz pode reflectir das superfícies próximas para produzir uma área mais focada de visibilidade. É por isso que, enquanto se olha para a superfície interna de uma colher, pode-se ver apenas o reflexo do que está mais próximo da superfície da colher – mesmo que ainda pareça menor. Além disso, se você colocar seu dedo dentro da colher, a superfície do espelho pode produzir dois ou três reflexos diferentes ao mesmo tempo.

Lente côncava vs. lente convexa

Lentes côncavas e convexas existem em objetos do cotidiano como óculos, contatos, binóculos e telescópios. De forma similar à ciência por trás da reflexão da luz em espelhos convexos e côncavos, existem também padrões de como a luz passa através de lentes côncavas e convexas para produzir uma imagem visível.

Lentes convexas

De acordo com a Manocha Academy, lentes convexas são chamadas lentes convergentes devido à sua capacidade de produzir imagens que são diminuídas, ampliadas ou introvertidas. A precisão com que uma imagem aparece através da lente convexa depende de quão próximo o objeto está do ponto focal da lente. Para qualquer lente convexa, existem pontos focais simétricos em ambos os lados da lente.

Como um objeto é produzido com precisão através de uma lente convexa é previsto com três princípios:

Princípio 1: Qualquer raio de luz que passa através de uma lente convexa é paralelo ao eixo principal, que é uma linha central que passa através do centro absoluto de uma lente esférica. Uma vez que a luz entra em contacto com a lente, a luz refracta e passa através do ponto focal do outro lado. Passando raios de luz que são paralelos ao eixo principal, o curso acima do objeto na frente da lente.

Princípio 2: Qualquer raio de luz que passa pelo centro de uma lente convexa continuará em uma linha reta do outro lado.
Princípio 3: Qualquer raio de luz que passe por um ponto focal do mesmo lado do objeto se refratará ao contatar a lente e se tornará paralelo ao eixo principal do outro lado.

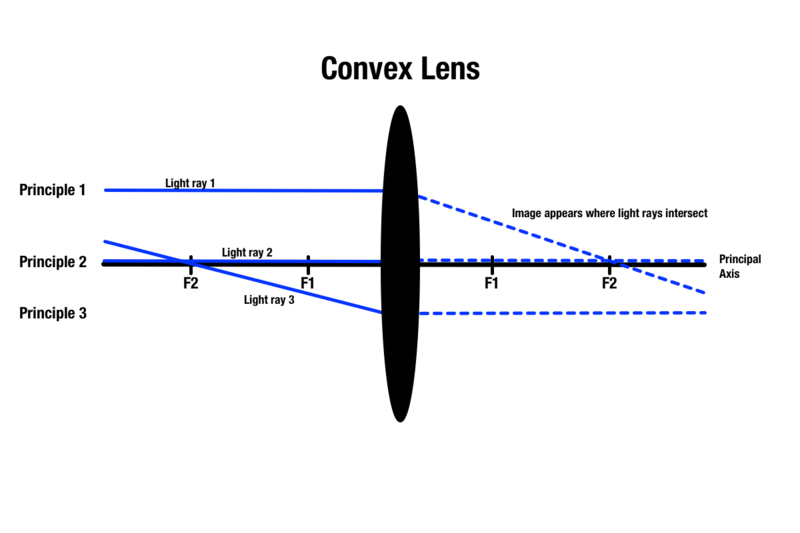
Embora existam três princípios para prever a qualidade da imagem através de uma lente convexa, apenas dois princípios podem ser aplicados a um objeto enquanto se desenha um diagrama de raios. Quaisquer dois princípios produzirão uma intersecção de luz no outro lado da lente, que indicará a área onde a imagem do objeto aparece.

Quanto mais afastado um objecto estiver de uma lente convexa, menor será a imagem do outro lado, e quanto mais próximo um objecto estiver da lente convexa, maior será o seu tamanho. Um objeto localizado depois do ponto focal mais próximo produz uma imagem maior atrás do objeto. Como aponta a Manocha Academy, este tipo de ampliação de lentes é usado para ferramentas ópticas como lupas.

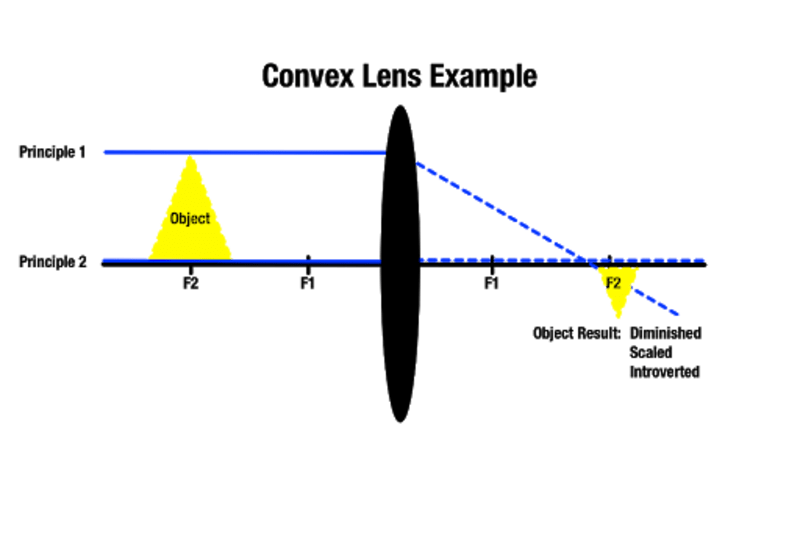
Dependente do ponto focal em que um objecto está localizado, é possível produzir uma imagem de tamanho aproximado. Também é possível criar imagens reais que não são visíveis se os raios de luz que passam nunca se cruzam porque são paralelos no outro lado. Neste caso, a imagem produzida existe a uma distância infinita.

Lentes côncavas

Ainda lente côncava terá um diâmetro mais espesso, e um centro mais fino uma vez que uma lente côncava é curvada para dentro. A forma das lentes côncavas permite que a luz se espalhe assim que entra em contacto com a lente, o que permite que os objectos virtuais apareçam mais pequenos. A capacidade da lente côncava de espalhar a luz faz dela uma lente ideal para ferramentas como lanternas, onde uma fonte central de luz pode ser usada sobre uma área maior da superfície.

Lentes côncavas produzem imagens com três princípios que são semelhantes às lentes convexas:

Princípio 1: Qualquer raio de luz que viaje acima do objeto e paralelo ao eixo principal se refratará ao contato com a lente e aparecerá como se estivesse vindo da direção do ponto focal mais próximo.

Princípio 2: Qualquer raio de luz que passe pelo centro da lente côncava passará sem refracção.
Princípio 3: Qualquer raio de luz dirigido para um ponto focal do outro lado da lente côncava irá refratar-se e tornar-se paralelo ao eixo principal.

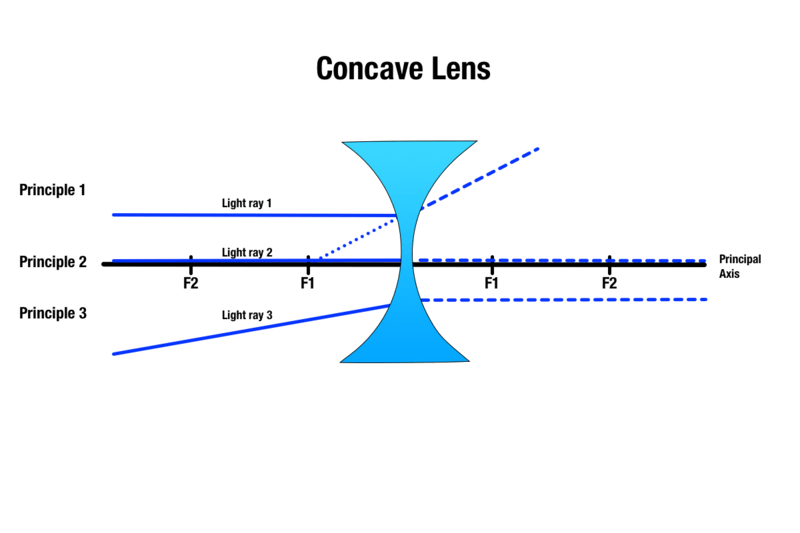
Embora o tamanho da imagem do objecto varie em função da distância do objecto a uma lente côncava, a imagem produzida é sempre virtual, vertical, mais pequena e aparece do mesmo lado da lente que o objecto.

Concave vs. convexa na escrita

As palavras côncava e convexa são opostas uma da outra, e descrevem essencialmente a forma dos objectos ou superfícies da mesma forma que nós contrastamos palavras como:

• Small vs. big
• Tall vs. short
• Slim vs. wide
• Round vs. flat

Porque palavras côncavas e convexas são palavras técnicas, usando-as de forma descritiva para prosa pode produzir uma interpretação mais metafórica ou abstracta para audiências casuais. O que isto significa é que se os escritores decidirem usar concava ou convexa fora do âmbito do seu uso típico, o escritor deve decidir o quão claro pretendem que a sua escrita seja.

Considerar o adjetivo

Um exemplo proeminente de uso côncavo ou convexo na literatura é considerar os escritos do autor americano David Foster Wallace (ou DFW para abreviar). O DFW é notório por seu estilo de escrita complexa e técnica – e sim, ele usou convexo e côncavo para descrever substantivos várias vezes. Wallace usa convexo e côncavo nos seguintes exemplos:

“Meu handeye estava bem, mas eu não era grande nem rápido, tinha um peito e pulsos quase côncavos tão finos que eu podia braceletá-los com um polegar e um dedo mindinho…”.

– “Ténis, Trigonometria, Tornados”: Um Menino do Meio-Oeste”, Revista Harper’s.

“…olhos de boneca que se abrem com o puxar de um cordão de coração, côncavo onde estou convexo.”

>

– “Ordem e Fluxo em Northampton”, Conjunções.

O ponto de usar exemplos DFW não é meramente para mostrar como os escritores têm usado convexo ou côncavo fora do contexto matemático, mas sim, para que os escritores considerem se o uso de termos técnicos ou abstratos é útil para comunicar claramente ao seu público.
No primeiro exemplo DFW, o uso de côncavo faz sentido porque ele está descrevendo a estrutura de algo. Mas, usar concavo e convexo para descrever substantivos não-objetivos, tais como sentimentos ou pensamentos, tende a obscurecer o significado do que estamos tentando explicar. O segundo exemplo do DFW caminha uma linha tênue enquanto usa convexo e côncavo porque seu uso é tanto literal quanto metafórico.

FAQ: Termos relacionados

O que é uma função?

Uma função é a equação de uma linha em um gráfico. Funções são diferentes para cada linha em um gráfico, mas elas tomam a forma geral de,

f(x) = x + 1

Com qualquer função de linha, a variável dependente é tipicamente f(x), enquanto qualquer variável desconhecida dentro da função é chamada de variável independente.

Qual é o domínio?

O domínio é um conjunto de variáveis independentes em um gráfico que corresponde à função de uma linha. Os domínios são importantes para entender porque eles localizam pontos específicos no gráfico que correspondem a qualquer saída real de uma equação.

Qual é o intervalo?

O intervalo de qualquer função representa qualquer valor possível ao longo dos eixos x ou y em um gráfico que produz um valor válido para a variável dependente. Todos os inteiros mínimos e máximos são identificados pela substituição de variáveis para os eixos x ou y.

O que é um intervalo?

Um intervalo é um conjunto de números que representam os números inteiros de uma linha, também conhecido como o domínio. Um intervalo fechado inclui dois pontos finitos de uma linha, onde a linha já não existe fora do intervalo de um número inteiro. Um intervalo aberto é um conjunto de números inteiros que não representam o fim absoluto do domínio de uma linha.

Test Yourself!

Veja quão bem você entende a diferença entre convexo e côncavo com as seguintes perguntas de múltipla escolha:

1. Enquanto olha para uma colher brilhante, você percebe que seu reflexo está de cabeça para baixo. A superfície da colher é uma superfície _________.
   a. Convexo
   b. Espelho
   c. Côncavo
   d. Metal
2. Em termos de funções gráficas, uma função convexa é por vezes chamada de convexa:
   a. Côncavo para cima
   b. Convexo para baixo
   c. Côncavo para baixo
   d. A e B
3. Qual das seguintes funções não descreve uma superfície côncava:
   a. Meia esfera côncava
   b. Lente do olho
   c. Tigela de cereais
   d. Hemisfério
4. Qual das seguintes não descreve uma superfície convexa:
   a. O personagem Stewie da Família Guy
   b. Esfera
   c. Espelho da garagem de estacionamento
   d. Futebol
5. Qual das seguintes formas não pode existir como um polígono côncavo:
   a. Pentágono
   b. Hexágono
   c. Triângulo
   d. Octógono

Respostas

1. C: Côncavo
2. D: A e B
3. D: Hemisfério
4. B: Esfera
5. C: Triângulo

Fontes:

1. Bourne, M. “Domínio e Alcance de uma Função”. Matemática Interativa, 4 de janeiro de 2019.
2. “Côncavo”. Merriam-Webster Dictionary, 2019.
3. “Côncavo.” The Oxford Dictionary of Word Histories, Ed. Chantrell, 2002, p. 110.
4. “Espelhos Côncavos e Convexos.” Manocha Academy, YouTube, 2019.
5. “Lente Côncava”: Definição &”Usos.” Study.com, 2019.
6. “Convex.” Merriam-Webster Dictionary, 2019.
7. “Lentes convexas e côncavas.” Manocha Academy, YouTube, 2019.
8. “Matemática / Entendendo Polígonos.” Learnhive Inc., 2018.
9. “Reflexão de um espelho côncavo.” UNSW Physics, YouTube, 2017.
10. Wallace, D.F. “Ténis, Trigonometria, Tornados”: Um Menino do Meio-Oeste.” Harper’s Magazine, 1991.
11. Wallace, D.F. “Ordem e Fluxo em Northampton.” Conjunctions, 1991.
12. Weisstein, Eric W. “Função Côncava”. MathWorld-A Wolfram Web Resource, n.d.
13. Weisstein, Eric W. “Função Convexa”. MathWorld-A Wolfram Web Resource, n.d.

O contador de palavras é uma ferramenta online dinâmica usada para contar palavras, caracteres, frases, parágrafos e páginas em tempo real, juntamente com a ortografia e verificação gramatical.