O Algoritmo Toom-Cook
>
Aqui aprendemos uma aplicação engenhosa de um algoritmo de dividir e conquistar combinado com álgebra linear para multiplicar grandes números, rapidamente. E uma introdução à notação big-O!
De facto este resultado é tão contra-intuitivo que o grande matemático Kolmogorov conjecturou um algoritmo tão rápido que não existia.
Parte 0: Multiplicação Longa é Multiplicação Lenta. (E uma Introdução à Notação Big-O)
Todos nós nos lembramos de aprender a multiplicar na escola. Na verdade, eu tenho uma confissão a fazer. Lembre-se, esta é uma zona sem julgamento 😉
Na escola, nós tivemos ‘brincadeiras molhadas’ quando estava chovendo muito difícil de brincar no playground. Enquanto outras crianças (normais/fun-loving/positivo-adjetivo-de-escolha) brincavam e brincavam, às vezes eu pegava uma folha de papel e multiplicava grandes números juntos, só para o inferno da coisa. A pura alegria da computação! Tivemos até uma competição de multiplicação, a ‘Super 144’, onde tivemos de multiplicar uma grade de 12 por 12 números (de 1 a 12) o mais rápido possível. Eu pratiquei isso religiosamente, na medida em que eu tinha minhas próprias fichas de prática pré-preparadas que eu fotocopiei, e depois usei em rotação. Eventualmente consegui reduzir meu tempo para 2 minutos e 1 segundo, no qual meu limite físico de rabiscos foi atingido.
Apesar dessa obsessão com a multiplicação, nunca me ocorreu que pudéssemos fazer melhor. Passei tantas horas multiplicando, mas nunca tentei melhorar o algoritmo.
Considerando multiplicar 103 por 222.
Calculamos 2 vezes 3 vezes 1 +2 vezes 0 vezes 10 + 2 vezes 1 vezes 100 + 20 vezes 3 vezes 1 + 20 vezes 0 vezes 10 + 20 vezes 1 vezes 100 = 22800
Em geral, para multiplicar para n dígitos, são necessárias operações de O(n²). A notação ‘big-O’ significa que, se fossemos representar graficamente o número de operações em função de n, o termo n² é realmente o que importa. A forma é essencialmente quadrática.
Hoje vamos realizar todos os nossos sonhos de infância e melhorar este algoritmo. Mas primeiro! Big-O espera-nos.
Big-O
Leia os dois gráficos abaixo
 >
>
>
Ask a mathematician, “are x² and x²+x^(1/3) the same?”, and they will probably vomit into their coffee cup and start crying, and mumbleble something about topology. Pelo menos, essa foi minha reação (no início), e eu mal sei nada sobre topologia.
Ok. Não são a mesma coisa. Mas o nosso computador não quer saber de topologia. Os computadores diferem no desempenho de tantas maneiras que nem consigo descrever porque não sei nada sobre computadores.
Mas não adianta afinar um rolo compressor. Se duas funções, para grandes valores de seus inputs, crescem na mesma ordem de grandeza, então para fins práticos que contém a maioria das informações relevantes.
No gráfico acima, vemos que as duas funções parecem bastante semelhantes para grandes inputs. Mas da mesma forma, x² e 2x² são semelhantes – o último é apenas duas vezes maior do que o primeiro. Em x = 100, um é 10.000 e um é 20.000. Isso significa que se podemos computar uma, provavelmente podemos computar a outra. Enquanto que uma função que cresce exponencialmente, digamos 10^x, a x = 100 já é muito maior do que o número de átomos no universo. (10¹⁰⁰ >>>>> 10⁸⁰ que é uma estimativa, o número Eddington, do número de átomos no universo de acordo com o meu Googling*).
*actualmente, eu usei DuckDuckGo.
Escrever inteiros como polinómios é muito natural e muito antinatural. Escrever 1342 = 1000 + 300 + 40 + 2 é muito natural. Escrevendo 1342 = x³+3x²+4x + 2, onde x = 10, é ligeiramente estranho.
Em geral, suponha que queremos multiplicar dois grandes números, escritos na base b, com n dígitos cada um. Escrevemos cada número de n dígitos como um polinômio. Se dividirmos o número de n dígitos em r peças, este polinômio tem termos n/r.
Por exemplo, vamos b = 10, r = 3, e nosso número é 142.122.912
Podemos transformar isto em
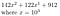
Isto funciona muito bem quando r = 3 e nosso número, escrito na base 10, tinha 9 dígitos. Se r não dividir perfeitamente n, então podemos simplesmente adicionar alguns zeros na frente. Novamente, isto é melhor ilustrado por um exemplo.
27134 = 27134 + 0*10⁵ = 027134, que representamos como
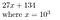
Por que isto pode ser útil? Para encontrar os coeficientes do polinômio P, se o polinômio é de ordem N, então, por amostragem em pontos N+1, podemos determinar seus coeficientes.
Por exemplo, se o polinômio x⁵ + 3x³ +4x-2, que é de ordem 5, for amostrado em 6 pontos, podemos então calcular o polinômio inteiro.
Intuitivamente, um polinômio de ordem 5 tem 6 coeficientes: o coeficiente de 1, x, x², x³, x⁴, x⁵. Dados 6 valores e 6 desconhecidos, podemos descobrir os valores.
(Se você conhece álgebra linear, você pode tratar as diferentes potências de x como vetores linearmente independentes, fazer uma matriz para representar a informação, inverter a matriz, e voila)
Polinômios de amostragem para determinar os coeficientes (Opcional)
Aqui olhamos com um pouco mais de profundidade para a lógica por trás da amostragem de um polinômio para deduzir seus coeficientes. Sinta-se livre para pular para a próxima seção.
O que vamos mostrar é que, se dois polinômios de grau N concordam em pontos N+1, então eles devem ser os mesmos. Ou seja, N+1 pontos especificam um polinômio de ordem N.
Considerar um polinômio de ordem 2. Isto é da forma P(z) = az² +bz + c. Pelo teorema fundamental da álgebra – sem vergonha, plug aqui, eu passei vários meses juntando uma prova disto, e depois escrevendo, aqui – este polinômio pode ser fatorizado. Isso significa que podemos escrevê-lo como A(z-r)(z-w)
Nota que em z = r, e em z = w, o polinômio avalia para 0. Dizemos que w e r são raízes do polinômio.
Agora mostramos que P(z) não pode ter mais do que duas raízes. Suponha que tivesse três raízes, a que chamamos w, r, s. Depois factorizamos o polinómio. P(z) = A(z-r)(z-w). Depois P(s) = A(s-r)(s-w). Isto não é igual a 0, pois a multiplicação de números não zero dá um número não zero. Isto é uma contradição porque nossa suposição original era que s era uma raiz do polinômio P.
Este argumento pode ser aplicado a um polinômio de ordem N de forma essencialmente idêntica.
Agora, suponha que dois polinômios P e Q de ordem N concordam em pontos N+1. Então, se eles forem diferentes, P-Q é um polinômio de ordem N que é 0 em pontos N+1. Pelo anterior, isto é impossível, pois um polinômio de ordem N tem no máximo N raízes. Assim, nossa suposição deve ter sido errada, e se P e Q concordam em pontos N+1 eles são o mesmo polinômio.
Vendo é acreditar: Exemplo trabalhado
Vejamos um número realmente enorme que chamamos p. Na base 10, p tem 24 dígitos (n=24), e nos dividiremos em 4 peças (r=4). n/r = 24/4 = 6
p = 292.103.243.859.143.157.364.152.
E deixe o polinômio representando-o ser chamado P,
P(x) = 292.103 x³ + 243.859 x² +143.157 x+ 364.152
com P(10⁶) = p.
>Como o grau deste polinômio é 3, podemos trabalhar todos os coeficientes a partir da amostragem em 4 lugares. Vamos sentir o que acontece quando o sampleamos em alguns pontos.
- P(0) = 364.152
- P(1) = 1.043.271
- P(-1) = 172.751
- P(2) = 3.962.726
Uma coisa impressionante é que todos estes têm 6 ou 7 dígitos. Isso é comparado com os 24 dígitos originalmente encontrados em p.
Multipliquemos p por q. Let q = 124.153.913.241.143.634.899.130, e
Q(x) = 124.153 x³ + 913.241 x²+143.634 x + 899.130
Calcular t=pq pode ser horrível. Mas em vez de o fazer directamente, tentamos calcular a representação polinomial de t, que rotulamos T. Como P é um polinómio de ordem r-1=3, e Q é um polinómio de ordem r-1 = 3, T é um polinómio de ordem 2r-2 = 6.
T(10⁶) = t = pq
T(10⁶) = P(10⁶)Q(10⁶)
O truque é que vamos trabalhar os coeficientes de T, em vez de multiplicarmos directamente p e q juntos. Então, calcular T(1⁰⁶) é fácil, porque para multiplicar por 1⁰⁶ basta colar 6 zeros na parte de trás. Somar todas as partes também é fácil porque a adição é uma ação de baixo custo para os computadores.
Para calcular os coeficientes de T, precisamos amostrar a 2r-1 = 7 pontos, porque é um polinômio de ordem 6. Nós provavelmente queremos escolher inteiros pequenos, por isso escolhemos
- T(0)=P(0)=P(0)= 364.152*899.130
- T(1)=P(1)Q(1)= 1.043.271*2.080.158
- T(2)=P(2)Q(2)= 3.962.726*5.832,586
- T(-1)=P(-1)Q(-1)= 172751*1544584
- T(-2)=P(-2)Q(-2)= -1.283.550*3.271,602
- T(3)=P(-3)Q(-3)= -5,757,369*5,335,266
Nota o tamanho de P(-3), Q(-3), P(2), Q(2) etc… Estes são todos números com aproximadamente n/r = 24/4 = 6 dígitos. Alguns são de 6 dígitos, outros de 7. Como n fica maior, esta aproximação fica cada vez mais razoável.
Até agora reduzimos o problema aos seguintes passos, ou algoritmo:
(1) Primeiro calcule P(0), Q(0), P(1), Q(1), etc (ação de baixo custo)
(2) Para obter nossos 2r-1= 7 valores de T(x), devemos agora multiplicar 2r-1 números de tamanho aproximado de n/r de comprimento de dígitos. Nomeadamente, devemos calcular P(0)Q(0), P(1)Q(1), P(-1)Q(-1), etc. (Ação de custo alto)
(3) Reconstruir T(x) a partir dos nossos pontos de dados. (Ação de baixo custo: mas será considerada mais tarde).
(4) Com a nossa T(x) reconstruída, avalie T(10⁶) neste caso
Isto leva a uma boa análise do tempo de execução desta abordagem.
Tempo de execução
Do acima, descobrimos que, ignorando temporariamente as ações de baixo custo (1) e (3), o custo de multiplicar dois n dígitos com o algoritmo do Toom obedecerá:
Foi o que vimos no exemplo trabalhado. Multiplicar cada P(0)Q(0), P(1)Q(1), etc. custa T(n/r) porque estamos a multiplicar dois números de comprimento aproximadamente n/r. Temos que fazer isso 2r-1 vezes, pois queremos amostrar T(x) – sendo um polinômio de ordem 2r-2 – em 2r-1 lugares.
Quão rápido é isso? Nós podemos resolver este tipo de equação explicitamente.

>
>
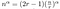
>>
>
>
Tudo o que resta agora é algum álgebra confusa
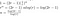 >
>>
>
Como houve alguns outros custos do processo de multiplicação da matriz (“remontagem”), e pela adição, não podemos realmente dizer que nossa solução é o tempo de execução exato, então concluímos que encontramos o big-O do tempo de execução
>
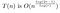
>>
>>
Optimização r
>
Este tempo de execução ainda depende de r. Fixar r, e estamos feitos. Mas a nossa curiosidade ainda não está satisfeita!
As n se tornam grandes, queremos encontrar um valor aproximadamente óptimo para a nossa escolha de r. Ou seja, queremos escolher um valor de r que muda para diferentes valores de n.
O fundamental aqui é que, com r variável, precisamos de prestar alguma atenção ao custo de remontagem – a matriz que realiza esta operação tem um custo de O(r²). Quando r foi fixo, não tivemos que olhar para isso, pois como n cresceu grande com r fixo, foram os termos envolvendo n que determinaram o crescimento em quanto cálculo foi necessário. Como a nossa escolha óptima de r vai ficar maior à medida que n fica maior, não podemos mais ignorar isto.
Esta distinção é crucial. Inicialmente a nossa análise escolheu um valor de r, talvez 3, talvez 3 bilhões, e depois olhou para o tamanho do big-O à medida que n crescia arbitrariamente grande. Agora, olhamos para o comportamento enquanto n cresce arbitrariamente grande e r cresce com n a algum ritmo que determinamos. Esta mudança de perspectiva olha para O(r²) como uma variável, enquanto que quando r foi mantido fixo, O(r²) era uma constante, embora não soubéssemos.
>
Então, atualizamos nossa análise de antes:
>
>
onde o O(r²) representa o custo da matriz de remontagem. Queremos agora escolher um valor de r para cada valor de n, o que minimiza aproximadamente esta expressão. Para minimizar, primeiro tentamos diferenciar com respeito a r. Isto dá a expressão de aspecto um pouco hediondo

Normalmente, para encontrar o ponto mínimo, definimos a derivada igual a 0. Mas esta expressão não tem um mínimo agradável. Em vez disso, encontramos uma solução ‘suficientemente boa’. Usamos r = r^(sqrt(logN)) como nosso valor de adivinhação. Graficamente, isto é muito próximo do mínimo. (No diagrama abaixo, o fator 1/1000 está lá para tornar o gráfico visível em uma escala razoável)
O gráfico abaixo mostra nossa função para T(N), escalada por uma constante, em vermelho. A linha verde está em x = 2^sqrt(logN) que foi o nosso valor estimado. ‘x’ toma o lugar de ‘r’, e em cada uma das três figuras, um valor diferente de N é usado.


>
 >
>>>
>
>
>
Esta é bastante convincente para mim que a nossa escolha foi uma boa escolha. Com esta escolha de r, podemos plugá-lo e ver como o nosso algoritmo final big-O:
 >
>>
>
onde simplesmente plugamos nosso valor para r, e usamos uma aproximação para log(2r-1)/log(r) que é muito precisa para grandes valores de r.
How Much of An Improvement?
Talvez eu não tenha visto este algoritmo quando eu era um rapazinho fazendo multiplicação era razoável. No gráfico abaixo, eu dou o coeficiente da nossa função big-O para ser 10 (para fins de demonstração) e o divido por x² (como a abordagem original da multiplicação era O(n²). Se a linha vermelha tende a 0, isso mostraria que nosso novo tempo de execução assimptóticamente faz melhor que O(n²).
E de fato, enquanto a forma da função mostra que nossa abordagem é eventualmente mais rápida, e eventualmente é muito mais rápida, temos que esperar até termos quase 400 números longos de dígitos para que isso seja o caso! Mesmo que o coeficiente fosse apenas 5, os números teriam de ter cerca de 50 dígitos para ver uma melhoria da velocidade.
>
 >
>>
>
Para o meu eu de 10 anos, multiplicar números de 400 dígitos seria um pouco exagerado! Manter um registo das várias chamadas recursivas da minha função também seria um pouco assustador. Mas para um computador fazendo uma tarefa em IA ou em física, este é um problema comum!
Quão profundo é este resultado?
O que eu adoro nesta técnica é que ela não é ciência de foguetes. Não é a matemática mais espantosa que há para ser descoberta. Em retrospectiva, talvez pareça óbvio!
Yet, este é o brilho e a beleza da matemática. Li que Kolmogorov conjecturou em um seminário que a multiplicação era fundamentalmente O(n²). Kolmogorov basicamente inventou muita teoria e análise de probabilidade moderna. Ele foi um dos grandes matemáticos do século XX. No entanto, quando se tratava deste campo não relacionado, revelou-se que havia todo um corpus de conhecimento à espera de ser descoberto, sentado mesmo debaixo do seu nariz e do de todos os outros!
De facto, os algoritmos Divide and Conquer vêm à mente bastante rapidamente hoje em dia, pois são tão vulgarmente utilizados. Mas eles são um produto da revolução informática, na medida em que é apenas com um vasto poder computacional que as mentes humanas têm focado especificamente na velocidade da computação como uma área da matemática digna de estudo por direito próprio.
É por isso que os matemáticos não estão apenas dispostos a aceitar a Hipótese de Riemann é verdadeira só porque parece que pode ser verdade, ou que P não é igual a NP só porque isso parece mais provável. O maravilhoso mundo da matemática sempre mantém uma capacidade de confundir nossas expectativas.
Na verdade, você pode encontrar maneiras ainda mais rápidas de se multiplicar. As melhores abordagens atuais usam transformadas rápidas de fourier. Mas vou guardar isso para outro dia 🙂
Deixe-me conhecer os seus pensamentos abaixo. Estou recentemente no Twitter como ethan_the_mathmo, você pode me seguir aqui.
Conheci este problema em um livro maravilhoso que estou usando chamado ‘The Nature of Computation’ pelos físicos Moore e Mertens, onde um dos problemas guia você através da análise do algoritmo do Toom.