Como ajudar alunos que lutam com problemas de palavras

“Eles conhecem a matemática. Eles simplesmente não conseguem fazer os problemas com a palavra. É a compreensão de leitura deles.”

Ms. Hartwell estava explicando porque seus alunos tinham lutado nos testes estaduais. Ela conhecia os seus alunos, e tinha feito uma ampla avaliação. Ela tinha certeza que as dificuldades deles eram um problema de alfabetização.

“Eu não entendo porque eles tornam a leitura tão difícil. As crianças já faziam um teste de artes linguísticas”.

Tinha sido combinado com a Sra. Hartwell (e outros em sua escola) como parte de um programa da cidade de Nova York para aumentar o desempenho em matemática. O objetivo era levar a matemática conceitual às escolas “Tier 1”. As escolas de nível 1 foram as que lideraram a cidade em três áreas. A renda mais baixa, as notas mais baixas nos testes e a maior porcentagem de alunos de cor.

Tinha ouvido a explicação de ‘alfabetização’ de outros professores do programa. E isso fazia sentido. Se os alunos sabiam a matemática, por que mais estavam lutando no teste, que tinha muitos problemas com palavras?

Mas havia um senão. Nos últimos três anos, a proficiência de alfabetização tinha passado de 30% para 40%, em toda a cidade. No mesmo período, as notas de matemática tinham permanecido, na sua maioria, planas.

Se isto fosse um problema de leitura, aumentos nos resultados de leitura deveriam desbloquear um crescimento explosivo em matemática. Além disso, a linguagem na palavra problemas simplesmente não parecia complicada o suficiente para causar problemas.

No período seguinte, eu estava programado para visitar a classe da Sra. Hartwell. Ela tinha planejado uma aula sobre problemas de palavras, para que eu pudesse ver o problema em primeira mão.

Problemas de Palavras em Andaimes

Os alunos se sentaram em mesas redondas, e ela ficou na frente. Ela e seus alunos tinham quadros brancos à mão.

Abriram os manuais na página 47 e ela leu um problema de palavras em voz alta. “Sarah tem 40 lbs. de cenouras para os seus cavalos. Se ela tem 100 cavalos, quantos quilos cada cavalo recebe?”

“OK classe, ela tem 40 libras que ela vai dar a cada cavalo. Então, de que operação precisamos?”

Apontou para um gráfico de âncora listando as ‘palavras-chave’ para cada operação. Cada’ estava no topo da lista de divisão.

“Divisão!” a classe respondeu.

“Certo. Então como dividimos um número pequeno por um número grande?”

“A classe estava quieta. A Sra. Hartwell desenhou um vinculum (casa de divisão longa) no seu quadro branco. Os alunos copiaram enquanto ela colocava 40 debaixo da casa e 100 fora.

“Agora 100 não cabe em 40, então precisamos adicionar uma casa decimal”. Ela mudou 40 para 40.0. “Quantas vezes 100 vai para 400?”

Alguns alunos chamaram “Quatro!”

“Exactamente. Agora, precisamos colocar uma casa decimal no nosso quociente também. Nossa resposta final é?”

A classe leu a resposta, “0.4”, fora de seu quadro branco.

A classe atribuiu um problema semelhante, e apontou para o cartaz “CUBES” na parede. “Lembre-se de fazer um círculo à volta dos números e encaixar as palavras-chave.”

Ela circulou enquanto os alunos trabalhavam. Alguns perguntaram onde colocar o decimal. Outros tiveram problemas para alinhar a parte da subtração da divisão longa. Alguns alunos trabalharam em pares, com um fazendo o cálculo, enquanto o outro copiou.

Ao final da aula, todos tinham a resposta correta em seu trabalho. “Vês?” A Sra. Hartwell comentou, “todos sabem a matemática”.

O que foi errado?

Embora este seja um exemplo extremo, muitos dos erros cometidos pela Sra. Hartwell são na verdade bastante comuns.

O excesso de andaimes ocorre quando damos demasiado apoio aos alunos. Enquanto é comum que os educadores se orgulhem de fornecer aos alunos “tanto apoio quanto eles precisam”, o excesso de andaimes é diferente.

O termo ‘andaime’ vem do trabalho de Lev Vygotsky. Ele cunhou o termo “Zona de Desenvolvimento Proximal”. O ZPD inclui coisas que estão apenas fora do alcance de um aprendiz. Eles não conseguem fazê-lo por si próprios, mas conseguem fazê-lo com apoio. Por ‘andaimes’, podemos mover estas habilidades para o conjunto de habilidades essenciais de um aprendiz.

O que muitas vezes é negligenciado é que andaimes só se aplicam a habilidades já no ZPD de um aprendiz. Há toda uma gama de competências que estão actualmente fora do alcance do aprendente. Quando tentamos scaffoldar estas competências, fazemos mais mal do que bem.

Um problema com o sobre andaime é que os alunos nunca internalizam as competências visadas. Quando ajudamos um aluno com algo fora do seu ZPD, ele sempre precisará da nossa ajuda. Pelo menos até identificarmos as habilidades intermediárias que estão no seu ZPD.

Outra questão é que o excesso de andaimes nos dá uma falsa sensação de sucesso. Neste caso, a Sra. Hartwell acreditava que seus alunos poderiam “fazer as contas” no problema da palavra. Na realidade, eles estavam apenas imitando suas ações. Não havia razão para acreditar que eles poderiam encontrar uma solução semelhante por si mesmos.

Ela também removeu todo o processo de ‘formulação’ do processo de solução de problemas. Muitos educadores pensam na compreensão e formulação como a mesma coisa, mas a formulação é uma competência matemática separada.

E pode ser apenas o ingrediente que falta na forma como você atualmente ensina problemas de palavras.

Recursos de sala de aula e aprendizagem profissional

>

Formulação: A chave para o sucesso com problemas de palavras

Formular problemas de palavras envolve compreendê-los. Mas isso vai além disso. Formulação é mais como tradução do que compreensão.

Quando um aluno lê um problema com uma palavra, primeiro tem de transformar letras em sons (descodificação). Depois, eles precisam entender o que as palavras significam (vocabulário). Eles precisam entender como as palavras se encaixam em uma frase (sintaxe). Finalmente, a compreensão vem da junção destas peças para fazer sentido.

Muitos alunos do 6º ano puderam ler o problema da Sra. Hartwell e facilmente entender que Sarah está distribuindo cenouras para os seus cavalos. Mas muito menos vai ligar a “partilha” de cenouras à divisão.

Esta é a parte que tropeça em muitos educadores. Parece tão óbvio para nós. “Ela está literalmente a dividir as cenouras. Como é que eles não viram que é a divisão.”

Não vêem. Se vissem, não se veriam gráficos de palavras-chave pendurados nas salas de aula de matemática. E tudo remonta a quando ensinamos operações pela primeira vez.

Porquê os alunos lutam com a Formulação

Muitos professores em muitas escolas ensinam aos alunos que a matemática é um assunto de fazer sentido. Mas em outras, a matemática é ensinada como uma disciplina de lembrar.

Um exemplo de ‘matemática como lembrança’ é quando os alunos memorizam fatos matemáticos. Mas os algoritmos também são sobre lembrar. Coloque 120 no topo de 47. Siga estes passos para adicionar, estes para subtrair subtrair e estes para multiplicar.

Os alunos podem repetir estes passos sem compreender o tamanho dos números ou mesmo o significado das operações.

Quando começamos com conceitos (usando modelos visuais ou sentenças numéricas), os alunos aprendem o significado das operações. Quando vamos directamente para um algoritmo, os alunos pensam nas operações como uma série de passos aleatórios.

Ano após ano, temos os alunos a lembrarem-se e a repetirem. Eles completam o mesmo algoritmo 30 vezes para os trabalhos de casa. Mude os números, e o processo permanece o mesmo. Mas dê-lhes um problema de palavras, e agora eles precisam fazer sentido.

O que os testes nos dizem sobre o Raciocínio

Podemos dar aos nossos alunos 10 problemas com o título “Divisão de Problemas de Palavras”, para facilitar. Eles não precisarão nem mesmo ler os problemas. Eles só precisam descobrir (ou adivinhar) qual número é o divisor e qual é o dividendo.

Mas quando os alunos fazem um teste de estado, o objetivo não é facilitar. O objetivo é avaliar o que eles podem fazer por conta própria.

Os fazedores de testes não querem dizer a eles qual operação usar. Eles até vão colocar palavras-chave para divisão e adição no mesmo problema. “Há 20 alunos na classe. Se cada criança tem três dólares, quanto é que eles têm no total?”

Então, quando os alunos lutam com problemas de palavras, não se trata apenas da palavra problemas. Geralmente significa que eles estão fazendo matemática pela memória. Precisamos ensiná-los que a matemática é sobre fazer sentido.

Os alunos precisam de estratégias e processos para resolver problemas de palavras

Uma parte do problema com um sistema como o CUBES é que ele se chama de estratégia, mas é realmente um processo.

Um processo é uma série de passos. Uma vez que você identifica um processo eficiente, você pode repeti-lo repetidamente sem pensar muito sobre ele. Algoritmos são um processo. Assim como é alinhado ‘o mais alto para o mais curto’ para a caminhada para o almoço.

Uma estratégia é diferente. As estratégias requerem uma compreensão profunda. E a capacidade de aplicar a compreensão em novas situações.

Não podemos preparar os alunos para cada cenário que eles vão encontrar em um problema de palavras. Alguns exigem que eles combinem diferentes habilidades matemáticas que eles nunca combinaram antes. Ou eles podem exigir que os alunos mudem a ordem dos passos para encontrar a solução correta.

Considere o seguinte:

Você tem 5 galões de suco para um evento escolar com 100 alunos. Se cada xícara contém 3 onças, quantos copos cada aluno pode beber? Quanto sobra.

Um processo de solução de problemas pode ajudar os alunos a começar a resolver este problema. “Identificar o que está a ser pedido.” “Considere que informação está sendo dada.”

Mas não há nenhum processo definido que possamos ensiná-los a realmente resolvê-lo. É aí que entra a estratégia. Eles precisam de converter unidades. Reconheça que estamos dividindo com restos, ao invés de dividir completamente. Eles também devem provavelmente reordenar as operações, dividindo o suco em copos antes de dividir pelo número de alunos.

Não há “truque” que leve os alunos até lá. Eles precisam entender o significado das operações. Eles precisam entender a matemática como um assunto de fazer sentido. E precisam de prática repetida aplicando pensamento estratégico a problemas de palavras.

O Processo Polya para Resolver Problemas de Palavras

George Pólya foi um influente matemático húngaro e professor de Stanford que encontrou um processo que poderia ser usado para resolver qualquer problema. Seu trabalho tocou inúmeros matemáticos e educadores, a maioria dos quais não sabe seu nome.

De fato, CUBES e outras chamadas estratégias de resolução de problemas são baseadas livremente em seu trabalho. O problema é que eles tentam simplificá-lo. No processo, eles removem qualquer coisa que se assemelhe a um pensamento profundo.

Polya acreditava que cada problema poderia ser resolvido em quatro passos: Compreender, Planear, Resolver e Reflectir. Eu acho que o processo original de quatro passos de Polya é muito bom para ser usado nas escolas.

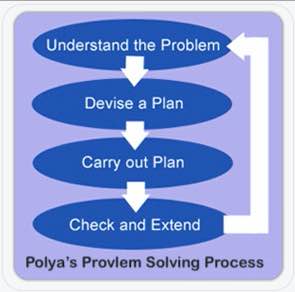Para entender o problema, identificamos quais informações são dadas e o que queremos encontrar. É daqui que vêm o ‘C’ e o ‘U’ em cubos. Se os alunos quiserem fazer um círculo à volta dos números e sublinhar a questão, tudo bem. Prefiro que eles os escrevam (com unidades) em um organizador gráfico, pelo menos no início. Isto ajuda-os a processar o que estão lendo. Também me ajuda, como professor, a avaliar a compreensão deles enquanto ando pela sala.

Próximo é a parte complicada. O ‘plano’ é onde nós formulamos o problema. Estamos pegando um cenário do mundo real e transformando-o em outra representação matemática.

O terceiro passo é Resolver. Se formulamos correctamente, é aqui que calculamos. Os alunos normalmente usam um algoritmo, mas eu encorajo o uso de equações e modelos visuais também.

Finalmente, os alunos olham para trás e verificam o seu trabalho. Eles também devem refletir sobre o seu processo. Se eu cometi um erro, porquê? Esta estratégia poderia ajudar-me a resolver problemas semelhantes no futuro?

Estratégias para resolver problemas de palavras

Ainda a um processo para abordar problemas de palavras é definitivamente útil. Mas não podemos fingir que a matemática significativa é aprendida apenas seguindo os passos seguintes. O objectivo dos problemas de palavras é expandir a matemática para além dos “factos matemáticos” e algoritmos.

Existem algumas estratégias úteis para ajudar os alunos na formulação. No início, eu ensino explicitamente uma série de estratégias diferentes.

Como ensino as estratégias, tenho alunos que resolvem problemas que vão bem com essa estratégia. Alguns tipos de problemas combinam muito bem com ‘Guess and Check’. Outros são mais adequados para ‘Tirar um Desenho’.

Eventualmente, eu lhes dou problemas de palavras desafiadoras que podem ser resolvidos de várias maneiras. Uma vez que eles têm as ferramentas em seus cintos de ferramentas, eles podem escolher qual é o melhor para a situação.

As estratégias de combinação também podem ser muito eficazes. Por exemplo, desenhar uma imagem pode muitas vezes ser útil para ajudar na formulação. Se um agricultor tem 18 fileiras de cenouras e 10 cenouras em cada fileira, um estudante pode começar desenhando o campo. Em algum momento, eles podem pensar “Uau, isto é um array”, e perceber que podem se multiplicar usando matemática mental, uma expressão, ou um algoritmo.

Outros tempos, os alunos podem usar modelos visuais para formular e resolver o problema.

Ajude seus alunos a resolver problemas de palavras desafiadoras

Se você é como muitos professores, você pode estar preocupado sobre como seus alunos vão lidar com tudo isso. Processos, estratégias, pensamento crítico… há muito envolvido.

Você pode até estar pensando que problemas de palavras pareciam mais fáceis antes deste artigo. Se assim for, peço desculpa.

A chave é não ficar sobrecarregado ao tentar fazer tudo de uma vez. Comece por resolver um simples problema de palavras usando o processo do Polya. Depois, introduza uma nova estratégia a cada semana. No final do ano, você ficará surpreso com o quão longe eles chegaram.

Talvez você esteja interessado em ir mais fundo na resolução criativa de problemas. Considere participar de um workshop prático de matemática ou trabalhar com um treinador online.

Se você estiver pronto para trazer algum Polya para sua sala de aula amanhã, este organizador gráfico é uma ótima maneira de começar. Ele irá percorrer os quatro passos do processo e ajudá-lo a identificar onde seus alunos estão saindo da pista.

Organizador de problemas de palavras livres

Sobre o Autor

Jeff Lisciandrello é o fundador da Room to Discover e um consultor educacional especializado em aprendizagem centrada no estudante. Seu projeto de 3 pontes para a aprendizagem ajuda as escolas a explorar práticas inovadoras dentro de ambientes tradicionais. Ele gosta de ajudar os educadores a abraçar abordagens baseadas em inquéritos e personalizadas para a instrução. Você pode se conectar com ele através do Twitter @EdTechJeff