Wanneer gegevens klaar zijn om te worden geanalyseerd, moet op basis van inspectie van de gegevens grondig worden beoordeeld of statistische methoden moeten worden gebruikt om ontbrekende gegevens te verwerken. Bell et al. wilden de omvang en behandeling van ontbrekende gegevens beoordelen in gerandomiseerde klinische onderzoeken die tussen juli en december 2013 zijn gepubliceerd in de BMJ, JAMA, Lancet, en New England Journal of Medicine . 95% van de 77 geïdentificeerde trials rapporteerden enige ontbrekende uitkomstgegevens. De meest gebruikte methode om ontbrekende gegevens in de primaire analyse te behandelen was complete case-analyse (45%), enkelvoudige imputatie (27%), modelgebaseerde methoden (bijvoorbeeld gemengde modellen of gegeneraliseerde schattingsvergelijkingen) (19%), en meervoudige imputatie (8%) .
Complete case-analyse
Complete case-analyse is statistische analyse op basis van deelnemers met een complete set uitkomstgegevens. Deelnemers met ontbrekende gegevens worden van de analyse uitgesloten. Zoals in de inleiding is beschreven, zal, als de ontbrekende gegevens MCAR zijn, de complete case-analyse een verminderde statistische power hebben vanwege de kleinere steekproefgrootte, maar de waargenomen gegevens zullen niet vertekend zijn. Wanneer de ontbrekende gegevens niet MCAR zijn, kan de schatting van het interventie-effect door de volledige gevalsanalyse gebaseerd zijn, d.w.z. dat er vaak een risico van overschatting van de baten en onderschatting van de schade zal zijn. Zie de paragraaf “Moet meervoudige toerekening worden gebruikt om ontbrekende gegevens te verwerken?” voor een meer gedetailleerde bespreking van de potentiële validiteit als de volledige gevalsanalyse wordt toegepast.
Enkelvoudige toerekening
Bij gebruik van enkelvoudige toerekening worden ontbrekende waarden vervangen door een waarde die volgens een bepaalde regel is gedefinieerd . Er zijn vele vormen van enkelvoudige toerekening, bijvoorbeeld laatste waarneming overgedragen (de ontbrekende waarden van een deelnemer worden vervangen door de laatst waargenomen waarde van de deelnemer), slechtste waarneming overgedragen (de ontbrekende waarden van een deelnemer worden vervangen door de slechtst waargenomen waarde van de deelnemer), en eenvoudige gemiddelde toerekening . Bij simple mean imputation worden ontbrekende waarden vervangen door het gemiddelde voor die variabele. Het gebruik van enkelvoudige toerekening leidt vaak tot een onderschatting van de variabiliteit omdat elke niet-waargenomen waarde in de analyse hetzelfde gewicht heeft als de bekende, waargenomen waarden . De geldigheid van enkelvoudige toerekening hangt niet af van de vraag of de gegevens MCAR zijn; enkelvoudige toerekening hangt veeleer af van specifieke veronderstellingen dat de ontbrekende waarden bijvoorbeeld identiek zijn aan de laatst waargenomen waarde . Deze aannames zijn vaak onrealistisch en single imputation is daarom vaak een potentieel vertekende methode en moet met grote voorzichtigheid worden gebruikt.
Multiple imputation
Multiple imputation is een valide algemene methode gebleken om ontbrekende gegevens in gerandomiseerd klinisch onderzoek te verwerken, en deze methode is beschikbaar voor de meeste soorten gegevens. In de volgende paragrafen beschrijven we wanneer en hoe meervoudige imputatie moet worden gebruikt.
Moet meervoudige imputatie worden gebruikt om ontbrekende gegevens te verwerken?
Redenen waarom meervoudige imputatie niet moet worden gebruikt om ontbrekende gegevens te verwerken
Is het geldig om ontbrekende gegevens te negeren?
Analyse van geobserveerde gegevens (volledige gevalsanalyse) waarbij de ontbrekende gegevens worden genegeerd, is in drie omstandigheden een geldige oplossing.
- a)
Complete case analysis kan als primaire analyse worden gebruikt als de percentages ontbrekende gegevens lager zijn dan ongeveer 5% (als vuistregel) en het onaannemelijk is dat bepaalde patiëntengroepen (bijvoorbeeld de zeer zieke of de zeer ‘gezonde’ deelnemers) specifiek in een van de vergeleken groepen voor follow-up verloren gaan . Met andere woorden, als het potentiële effect van de ontbrekende gegevens te verwaarlozen is, kunnen de ontbrekende gegevens in de analyse worden genegeerd . In geval van twijfel kunnen best-worst-case en worst-best-case gevoeligheidsanalyses worden gebruikt: eerst wordt een best-worst-case dataset gegenereerd waarbij wordt aangenomen dat alle deelnemers die in de ene groep (groep 1) voor follow-up verloren zijn gegaan, een gunstig resultaat hebben gehad (bijvoorbeeld geen ernstig ongewenst voorval hebben gehad); en dat alle deelnemers in de andere groep (groep 2) die ontbrekende resultaten hebben gehad, een schadelijk resultaat hebben gehad (bijvoorbeeld een ernstig ongewenst voorval hebben gehad) . Vervolgens wordt een “worst-best-case”-dataset gegenereerd waarbij wordt aangenomen dat alle deelnemers die in groep 1 voor follow-up verloren zijn gegaan, een schadelijk resultaat hebben gehad, en dat alle deelnemers die in groep 2 voor follow-up verloren zijn gegaan, een gunstig resultaat hebben gehad. Indien continue uitkomsten worden gebruikt, kan een “gunstig resultaat” het groepsgemiddelde plus 2 standaarddeviaties (of 1 standaarddeviatie) van het groepsgemiddelde zijn, en een “schadelijk resultaat” het groepsgemiddelde min 2 standaarddeviaties (of 1 standaarddeviatie) van het groepsgemiddelde. Voor gedichotomiseerde gegevens zullen deze best-worst en worst-best case gevoeligheidsanalyses dan het bereik van de onzekerheid als gevolg van ontbrekende gegevens laten zien, en als dit bereik geen kwalitatief tegenstrijdige resultaten oplevert, kunnen de ontbrekende gegevens worden genegeerd. Voor continue gegevens geeft imputatie met 2 SD een mogelijke bandbreedte van onzekerheid aan gegeven 95% van de waargenomen gegevens (indien normaal verdeeld).
- b)
Als alleen voor de afhankelijke variabele waarden ontbreken en er geen hulpvariabelen (variabelen die niet in de regressieanalyse zijn opgenomen, maar wel gecorreleerd zijn met een variabele met ontbrekende waarden en/of verband houden met de missingness daarvan) zijn geïdentificeerd, kan een volledige gevalsanalyse als primaire analyse worden gebruikt en hoeven er geen specifieke methoden te worden gebruikt om de ontbrekende gegevens te verwerken. Er wordt geen extra informatie verkregen door bijvoorbeeld meervoudige toerekening, maar de standaardfouten kunnen toenemen als gevolg van de onzekerheid die door de meervoudige toerekening wordt geïntroduceerd .
- c)
Zoals hierboven vermeld (zie Methoden voor de behandeling van ontbrekende gegevens), zou het ook geldig zijn alleen een volledige gevalsanalyse uit te voeren als het vrij zeker is dat de gegevens MCAR zijn (zie Inleiding). Het komt betrekkelijk zelden voor dat het zeker is dat de gegevens MCAR zijn. Het is mogelijk de hypothese dat de gegevens MCAR zijn te testen met de test van Little , maar het kan onverstandig zijn voort te bouwen op tests die niet significant bleken te zijn. Als er dus gerede twijfel is of de gegevens MCAR zijn, zelfs als Little’s test niet significant is (de nulhypothese dat de gegevens MCAR zijn niet verwerpen), dan mag niet van MCAR worden uitgegaan.
Zijn de percentages ontbrekende gegevens te groot?
Als grote percentages gegevens ontbreken, moet worden overwogen om gewoon de resultaten van de volledige case-analyse te rapporteren en dan duidelijk de daaruit voortvloeiende interpretatieve beperkingen van de proefresultaten te bespreken. Indien meervoudige imputaties of andere methoden worden gebruikt om ontbrekende gegevens te verwerken, zou dit erop kunnen wijzen dat de resultaten van de proef bevestigend zijn, wat niet het geval is indien het aantal ontbrekende gegevens aanzienlijk is. Als de percentages ontbrekende gegevens voor belangrijke variabelen zeer groot zijn (bijvoorbeeld meer dan 40%), mogen de resultaten van de proef alleen worden beschouwd als hypothesegenererende resultaten . Een zeldzame uitzondering is het geval waarin het onderliggende mechanisme achter de ontbrekende gegevens als MCAR kan worden omschreven (zie bovenstaande paragraaf).
Lijken zowel de MCAR- als de MAR-aanname ongeloofwaardig?
Als de MAR-aanname op grond van de kenmerken van de ontbrekende gegevens ongeloofwaardig lijkt, dan bestaat het risico dat de resultaten van de proef vertekend zijn als gevolg van “incomplete outcome data bias” en kan geen enkele statistische methode met zekerheid rekening houden met deze potentiële vertekening . De geldigheid van methoden die worden gebruikt om met MNAR-gegevens om te gaan, vereist bepaalde veronderstellingen die niet op basis van waargenomen gegevens kunnen worden getoetst. Gevoeligheidsanalyses van de “best worst case” en “worst best case” kunnen het volledige theoretische bereik van onzekerheid laten zien en conclusies moeten aan dit bereik van onzekerheid worden gerelateerd. De beperkingen van de analyses moeten grondig worden besproken en overwogen.
Is de uitkomstvariabele met ontbrekende waarden continu en is het analytische model gecompliceerd (bv. met interacties)?
In deze situatie kan worden overwogen de directe maximale-waarschijnlijkheidsmethode te gebruiken om de problemen van modelcompatibiliteit tussen het analytische model en het meervoudige-imputatiemodel te vermijden, wanneer het eerste algemener is dan het laatste. In het algemeen kunnen directe maximale-waarschijnlijkheidsmethoden worden gebruikt, maar voor zover wij weten zijn er momenteel alleen commercieel beschikbare methoden voor continue variabelen.
Wanneer en hoe meervoudige imputaties gebruiken
Als aan geen van de “Redenen waarom meervoudige imputatie niet mag worden gebruikt om ontbrekende gegevens te verwerken” van hierboven is voldaan, kan meervoudige imputatie worden gebruikt. In de literatuur zijn de laatste decennia verschillende procedures voorgesteld om met ontbrekende gegevens om te gaan. We hebben de bovengenoemde overwegingen van statistische methoden om met ontbrekende gegevens om te gaan, geschetst in fig. 1.
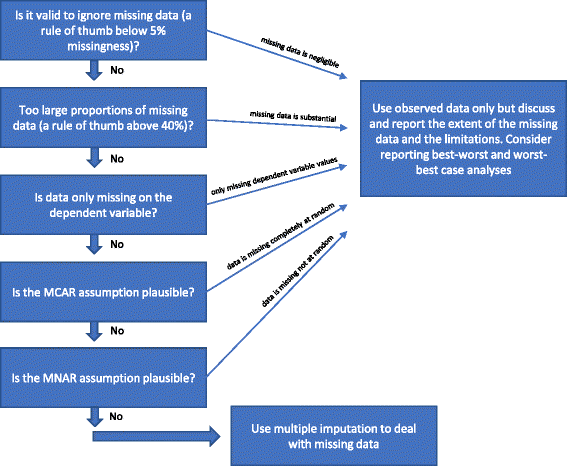
Flowchart: wanneer moet meervoudige toerekening worden gebruikt om ontbrekende gegevens te verwerken bij de analyse van resultaten van gerandomiseerde klinische onderzoeken
Meervoudige toerekening is ontstaan in het begin van de jaren zeventig en heeft in de loop der jaren aan populariteit gewonnen. Meervoudige toerekening is een statistische techniek op basis van simulatie voor het verwerken van ontbrekende gegevens. Meervoudige toerekening bestaat uit drie stappen:
-
Imputatiestap. Een “imputatie” vertegenwoordigt in het algemeen één reeks plausibele waarden voor ontbrekende gegevens – meervoudige imputatie vertegenwoordigt meerdere reeksen plausibele waarden . Bij meervoudige imputatie worden ontbrekende waarden geïdentificeerd en vervangen door een willekeurige steekproef van plausibele imputaties van waarden (voltooide datasets). Meervoudige volledige datasets worden gegenereerd via een gekozen imputatiemodel. Op theoretische gronden worden vijf geïmputeerde datasets traditioneel als voldoende beschouwd, maar 50 datasets (of meer) lijken de voorkeur te verdienen om de steekproefvariabiliteit van het imputatieproces te beperken. De gewenste analyse wordt afzonderlijk uitgevoerd voor elke dataset die tijdens de imputatiestap wordt gegenereerd. Hierbij worden bijvoorbeeld 50 analyseresultaten geconstrueerd.
-
Poolingstap. De resultaten van elke voltooide gegevensanalyse worden gecombineerd tot een enkel meervoudig imputatieresultaat . Het is niet nodig een gewogen meta-analyse uit te voeren, aangezien alle zeg 50 analyseresultaten worden geacht hetzelfde statistische gewicht te hebben.
Het is van groot belang dat er ofwel compatibiliteit is tussen het imputatiemodel en het analysemodel, ofwel dat het imputatiemodel algemener is dan het analysemodel (bijvoorbeeld dat het imputatiemodel meer onafhankelijke covariaten omvat dan het analysemodel) . Bijvoorbeeld, als het analysemodel significante interacties heeft, dan moet het imputatiemodel deze ook omvatten , als het analysemodel een getransformeerde versie van een variabele gebruikt, dan moet het imputatiemodel dezelfde transformatie gebruiken , enz.
Verschillende soorten meervoudige imputatie
Er bestaan verschillende soorten meervoudige imputatiemethoden. Wij zullen ze voorstellen volgens hun toenemende graad van complexiteit: 1) regressieanalyse met één waarde; 2) monotone imputatie; 3) geketende vergelijkingen of de Markov chain Monte Carlo (MCMC)-methode. In de volgende paragrafen zullen wij deze verschillende meervoudige imputatiemethoden beschrijven en aangeven hoe tussen deze methoden kan worden gekozen.
Een regressieanalyse met één variabele omvat een afhankelijke variabele en de stratificatievariabelen die bij de randomisatie worden gebruikt. De stratificatievariabelen omvatten vaak een centrumindicator als het om een multicentrisch onderzoek gaat en gewoonlijk een of meer aanpassingsvariabelen met prognostische informatie die gecorreleerd zijn met de uitkomst. Wanneer een continue afhankelijke variabele wordt gebruikt, kan ook een uitgangswaarde van de afhankelijke variabele worden opgenomen. Zoals vermeld onder “Redenen waarom geen statistische methoden mogen worden gebruikt om ontbrekende gegevens te verwerken”, moet, indien alleen voor de afhankelijke variabele waarden ontbreken en geen hulpvariabelen zijn geïdentificeerd, een volledige gevalsanalyse worden uitgevoerd en mogen geen specifieke methoden worden gebruikt om de ontbrekende gegevens te verwerken. Indien hulpvariabelen zijn geïdentificeerd, kan een imputatie van één variabele worden uitgevoerd. Als er significante missingness zijn op de uitgangsvariabele van een continue variabele, kan een volledige gevalsanalyse vertekende resultaten opleveren. Daarom wordt in alle gevallen een imputatie met één variabele (al dan niet met hulpvariabelen) uitgevoerd als alleen de uitgangsvariabele ontbreekt.
Als zowel de afhankelijke variabele als de uitgangsvariabele ontbreken en de missingness monotoon is, wordt een monotone imputatie uitgevoerd. Veronderstel een gegevensmatrix waarin patiënten worden voorgesteld door rijen en variabelen door kolommen. De missingness van een dergelijke gegevensmatrix wordt monotoon genoemd als de kolommen ervan zo kunnen worden geordend dat voor elke patiënt (a) als een waarde ontbreekt, alle waarden rechts van die positie ook ontbreken, en (b) als een waarde wordt waargenomen, alle waarden links van die waarde ook worden waargenomen. Als de missingness monotoon is, is de methode van meervoudige toerekening ook betrekkelijk eenvoudig, zelfs als meer dan één variabele ontbrekende waarden heeft. In dat geval is het relatief eenvoudig om de ontbrekende gegevens toe te rekenen met behulp van sequentiële regressie-imputatie, waarbij de ontbrekende waarden voor elke variabele tegelijk worden toegerekend. Veel statistische pakketten (bijvoorbeeld STATA) kunnen analyseren of de missingness monotoon is of niet.
Indien de missingness niet monotoon is, wordt een meervoudige imputatie uitgevoerd met behulp van de chained equations of de MCMC-methode. Hulpvariabelen worden in het model opgenomen als zij beschikbaar zijn. In fig. 2 is samengevat hoe tussen de verschillende meervoudige imputatiemethoden kan worden gekozen.
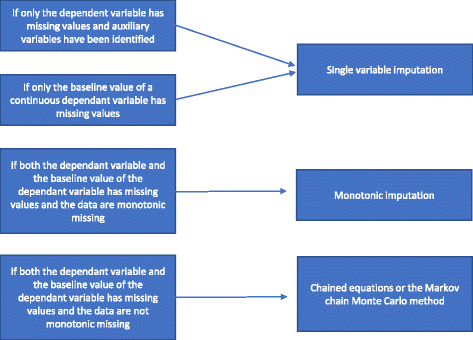
Flowchart van meervoudige imputatie
Volledige informatie maximale waarschijnlijkheid
Volledige informatie maximale waarschijnlijkheid is een alternatieve methode om met ontbrekende gegevens om te gaan. Het principe van de maximale waarschijnlijkheidsschatting is parameters van de gezamenlijke verdeling van uitkomst (Y) en covariaten (X1,…, Xk) te schatten die, indien waar, de kans op waarneming van de werkelijk waargenomen waarden zo groot mogelijk zouden maken. Indien bij een bepaalde patiënt waarden ontbreken, kan de waarschijnlijkheid worden verkregen door de gebruikelijke waarschijnlijkheid te sommeren over alle mogelijke waarden van de ontbrekende gegevens, op voorwaarde dat het mechanisme van de ontbrekende gegevens negeerbaar is. Deze methode wordt aangeduid als full information maximum likelihood .
Volledige informatie maximale waarschijnlijkheid heeft zowel sterke punten als beperkingen ten opzichte van meervoudige imputatie.
Sterke punten van volledige informatie maximale waarschijnlijkheid ten opzichte van meervoudige imputatie
- 1)
Het is eenvoudiger te implementeren, d.w.z. het is niet nodig om verschillende stappen te doorlopen zoals bij het gebruik van meervoudige imputatie.
- 2)
In tegenstelling tot meervoudige imputatie heeft volledige informatie maximale waarschijnlijkheid geen potentiële problemen met incompatibiliteit tussen het imputatiemodel en het analysemodel (zie ‘Meervoudige imputatie’). De geldigheid van de meervoudige imputatieresultaten zal twijfelachtig zijn indien er een incompatibiliteit bestaat tussen het imputatiemodel en het analysemodel, of indien het imputatiemodel minder algemeen is dan het analysemodel .
- 3)
Bij meervoudige imputatie worden alle ontbrekende waarden in elke gegenereerde dataset (imputatiestap) vervangen door een willekeurige steekproef van plausibele waarden. Tenzij “a random seed” is gespecificeerd, zullen bijgevolg telkens wanneer een meervoudige imputatieanalyse wordt uitgevoerd, andere resultaten worden getoond. Analyses waarbij gebruik wordt gemaakt van volledige informatie op basis van maximale waarschijnlijkheid op dezelfde gegevensreeks zullen telkens wanneer de analyse wordt uitgevoerd dezelfde resultaten opleveren, en de resultaten zijn dus niet afhankelijk van een “random number seed”. Indien de random seed waarde echter in het statistische analyseplan wordt gedefinieerd, kan dit probleem worden opgelost.
Beperkingen van full information maximum likelihood ten opzichte van meervoudige imputatie
De beperkingen van het gebruik van full information maximum likelihood ten opzichte van het gebruik van meervoudige imputatie, is dat het gebruik van full information maximum likelihood alleen mogelijk is met speciaal ontworpen software . Er is speciaal ontworpen voorbereidende software ontwikkeld, maar de meeste daarvan missen de mogelijkheden van commercieel ontworpen statistische software (bijvoorbeeld STATA, SAS, of SPSS). In STATA (met behulp van het SEM-commando) en SAS (met behulp van het PROC CALIS-commando) is het mogelijk gebruik te maken van full information maximum likelihood, maar alleen wanneer continue afhankelijke (uitkomst)variabelen worden gebruikt. Voor logistische regressie en Cox-regressie is Mplus het enige commerciële pakket dat maximale waarschijnlijkheid met volledige informatie voor ontbrekende gegevens biedt.
Een andere potentiële beperking bij het gebruik van maximale waarschijnlijkheid met volledige informatie is dat er een onderliggende aanname van multivariate normaliteit kan zijn. Niettemin kunnen schendingen van de multivariate normaliteitsveronderstelling niet zo belangrijk zijn, zodat het aanvaardbaar kan zijn om binaire onafhankelijke variabelen in de analyse op te nemen .
Wij hebben in Additional file 1 een programma (SAS) opgenomen dat een volledige speelgoed-dataset produceert met inbegrip van verschillende analyses van deze gegevens. Tabel 1 en tabel 2 tonen de output en hoe verschillende methoden die ontbrekende gegevens behandelen verschillende resultaten opleveren.
Panelwaarden regressieanalyse
Panelgegevens staan meestal in een zogenaamd breed databestand, waarbij de eerste rij de namen van de variabelen bevat, en de daaropvolgende rijen (een voor elke patiënt) de overeenkomstige waarden. De uitkomst wordt weergegeven door verschillende variabelen – één voor elke geplande, getimede meting van de uitkomst. Om de gegevens te analyseren, moet het bestand worden omgezet in een zogenaamd lang bestand met één record per geplande uitkomstmeting, met inbegrip van de uitkomstwaarde, het tijdstip van de meting en een kopie van alle andere variabelewaarden, met uitzondering van die van de uitkomstvariabele. Om de correlaties binnen de patiënt tussen de getimede uitkomstmetingen te behouden, is het gebruikelijk een meervoudige invoer van het gegevensbestand in zijn brede vorm uit te voeren, gevolgd door een analyse van het resulterende bestand nadat het naar zijn lange vorm is geconverteerd. Proc. mixed (SAS 9.4) kan worden gebruikt voor de analyse van continue uitkomstwaarden en proc. glimmix (SAS 9.4) voor andere soorten uitkomstwaarden. Omdat deze procedures de directe maximale waarschijnlijkheidsmethode toepassen op de uitkomstgegevens, maar gevallen met ontbrekende covariaatwaarden negeren, kunnen de procedures direct worden gebruikt wanneer alleen waarden van afhankelijke variabelen ontbreken en er geen goede hulpvariabelen beschikbaar zijn. Anders moet na een meervoudige berekening proc. mixed of proc. glimmix (afhankelijk van welke van beide geschikt is) worden gebruikt. Uiteraard is een soortgelijke aanpak mogelijk met andere statistische pakketten.
Gevoeligheidsanalyses
Gevoeligheidsanalyses kunnen worden gedefinieerd als een reeks analyses waarbij op een andere manier met de gegevens wordt omgegaan dan bij de primaire analyse. Gevoeligheidsanalyses kunnen laten zien hoe andere aannames dan die in de primaire analyse de verkregen resultaten beïnvloeden. Gevoeligheidsanalyses moeten van tevoren worden vastgesteld en beschreven in het plan voor de statistische analyse, maar aanvullende post hoc gevoeligheidsanalyses kunnen gerechtvaardigd en geldig zijn. Wanneer de mogelijke invloed van ontbrekende waarden onduidelijk is, bevelen wij de volgende gevoeligheidsanalyses aan:
-
Wij hebben reeds het gebruik van best-worst en worst-best case gevoeligheidsanalyses beschreven om de bandbreedte van de onzekerheid als gevolg van ontbrekende gegevens aan te geven (zie Beoordeling of methoden moeten worden gebruikt om ontbrekende gegevens te verwerken). Onze vorige beschrijving van de best-worst en worst-best case gevoeligheidsanalyses had betrekking op ontbrekende gegevens over een dichotome of een continue afhankelijke variabele, maar deze gevoeligheidsanalyses kunnen ook worden gebruikt wanneer gegevens ontbreken over stratificatievariabelen, basislijnwaarden, enz. De potentiële invloed van ontbrekende gegevens moet voor elke variabele afzonderlijk worden beoordeeld, d.w.z. dat er voor elke variabele (afhankelijke variabele, uitkomstindicator en stratificatievariabelen) met ontbrekende gegevens één best-worst en één worst-best case scenario moet zijn.
-
Als besloten wordt dat bijvoorbeeld meervoudige imputaties moeten worden gebruikt, dan moeten deze resultaten het primaire resultaat van de gegeven uitkomst zijn. Elke primaire regressieanalyse moet altijd worden aangevuld met een overeenkomstige analyse van waargenomen (of beschikbare) gevallen.
Wanneer mixed-effectmethoden worden gebruikt
Het gebruik van een multicentrische proefopzet zal vaak nodig zijn om binnen een redelijk tijdsbestek een voldoende aantal proefdeelnemers te werven. Een multicentrische proefopzet biedt ook een betere basis voor de latere generalisatie van de bevindingen . Gebleken is dat de meest gebruikte analysemethoden in gerandomiseerd klinisch onderzoek goed werken bij een klein aantal centra (waar binaire afhankelijke uitkomsten worden geanalyseerd) . Bij een relatief groot aantal centra (50 of meer) is het vaak optimaal om “centrum” als willekeurig effect te gebruiken en analysemethoden met gemengd effect toe te passen. Ook bij de analyse van longitudinale gegevens zal het vaak zinvol zijn gebruik te maken van analysemethoden met gemengde effecten. In sommige omstandigheden kan het geldig zijn om het “random effect”-covariaat (bijvoorbeeld “centrum”) tijdens de imputatiestap als een covariaat met een vast effect op te nemen en vervolgens tijdens de analysestap gebruik te maken van een gemengde-modelanalyse of gegeneraliseerde schattingsvergelijkingen (GEE). De toepassing van een mixed-effects model (met bijvoorbeeld “centrum” als willekeurig effect) houdt echter in dat bij de modellering van de meervoudige imputatie rekening moet worden gehouden met de gelaagde structuur van de gegevens. Nu is er niet direct commerciële software beschikbaar om dit te doen. Men kan echter gebruik maken van het REALCOME-pakket dat met STATA kan worden gekoppeld. De interface exporteert de gegevens met ontbrekende waarden van STATA naar REALCOM waar de imputatie wordt uitgevoerd rekening houdend met het multilevel-karakter van de gegevens en met gebruikmaking van een MCMC-methode die continue variabelen omvat en door gebruikmaking van een latent normaal model ook een goede behandeling van discrete gegevens mogelijk maakt. De geïmputeerde datasets kunnen vervolgens worden geanalyseerd met het STATA-commando “mi estimate:”, dat kan worden gecombineerd met het “mixed”-statement (voor een continue uitkomst) of het “meqrlogit”-statement voor een binaire of ordinale uitkomst in STATA . Bij de analyse van paneldata kan men echter gemakkelijk geconfronteerd worden met een situatie waarin de gegevens drie of meer niveaus omvatten, bijvoorbeeld metingen binnen dezelfde patiënt (niveau-1), patiënten binnen centra (niveau-2), en centra (niveau-3) . Om niet verwikkeld te raken in een nogal ingewikkeld model dat kan leiden tot gebrek aan convergentie of instabiele standaardfouten en waarvoor geen commerciële software beschikbaar is, wordt aanbevolen het centrumeffect als vast te behandelen (rechtstreeks of na samenvoeging van kleine centra tot één of meer centra van passende grootte, volgens een procedure die in het plan voor de statistische analyse moet worden voorgeschreven) of centrum als covariaat uit te sluiten. Indien de randomisatie naar centrum is gestratificeerd, zal deze laatste aanpak leiden tot een opwaartse vertekening van de standaardfouten, hetgeen resulteert in een enigszins conservatieve testprocedure.