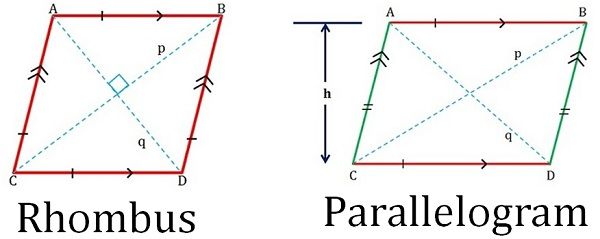
In de meetkunde zijn er vele soorten vierhoeken: parallellogram, ruit, vierkant, rechthoek, trapezium en vlieger, die gemeenschappelijke kenmerken hebben, waardoor mensen moeite hebben om deze figuren te begrijpen. Een ruit kan worden omschreven als een schuin vierkant, waarvan de aanliggende zijden gelijk zijn. Een parallellogram daarentegen is een schuine rechthoek met twee evenwijdige tegenover elkaar liggende zijden.
Het fundamentele verschil tussen ruit en parallellogram ligt in hun eigenschappen, d.w.z. dat alle zijden van een ruit even lang zijn, terwijl een parallellogram een rechtlijnige figuur is waarvan de tegenover elkaar liggende zijden evenwijdig zijn.
Inhoud: Rhombus Vs Parallelogram
- Vergelijkingsdiagram
- Definitie
- Key verschillen
- Conclusie
Vergelijkingsdiagram
| Grondstof voor vergelijking | Rhombus | Parallelogram |
|---|---|---|
| Betekenis | Rhombus verwijst naar een platvormige, vierzijdige figuur waarvan alle zijden congruent zijn. | Een parallellogram is een vierzijdige vlakke figuur, waarvan de tegenover elkaar liggende zijden evenwijdig aan elkaar zijn. |
| Gelijke zijden | Alle vier zijden zijn even lang. | Oppositieve zijden zijn even lang. |
| Diagonalen | De diagonalen snijden elkaar in rechte hoeken en vormen zo een schalen driehoek. | De diagonalen snijden elkaar in twee congruente driehoeken. |
| Area | (pq)/2, waarbij p en q de diagonalen zijn | bh, waarbij b = basis en h = hoogte |
| Perimeter | 4 a, waarbij a = zijde | 2 (a+b), waarbij a = zijde, b = basis |
Definitie van Rhombus
Een vierhoek waarvan de lengte van de zijden congruent zijn, wordt een rhombus genoemd. Hij is plat en heeft vier zijden; de tegenover elkaar liggende zijden zijn evenwijdig aan elkaar (zie onderstaande figuur).
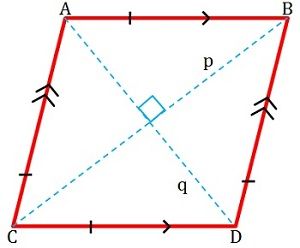De tegenover elkaar liggende hoeken van een ruit zijn gelijk, d.w.z. van dezelfde graad. De diagonalen staan op 90 graden (rechte hoek), dus loodrecht op elkaar en vormen twee gelijkzijdige driehoeken. De aanliggende zijden zijn supplementair, wat betekent dat de som van hun afmetingen gelijk is aan 180 graden. Het is ook bekend als een gelijkzijdige parallellogram.
Definitie van Parallellogram
Een parallellogram, zoals de naam al doet vermoeden, is een wordt beschreven als een platvormige figuur, met vier zijden waarvan de reeks tegenover elkaar liggende zijden evenwijdig en congruent zijn (zie onderstaande figuur).
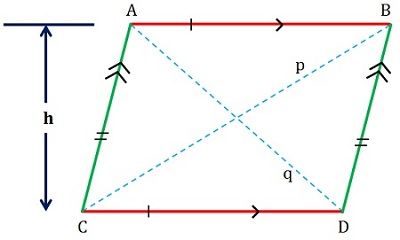De maat van de tegenover elkaar liggende hoeken is gelijk en de opeenvolgende hoeken zijn supplementair, d.w.z. dat de som van hun maat gelijk is aan 180 graden. De diagonalen snijden elkaar, zodat twee congruente driehoeken ontstaan.
Key verschillen tussen ruit en parallellogram
Het verschil tussen ruit en parallellogram kan duidelijk worden gemaakt op de volgende gronden:
- Wij definiëren ruit als een vierzijdige vierhoek waarvan de lengte van alle zijden congruent zijn. Een parallellogram is een vierzijdig platvormig figuur, waarvan de overstaande zijden evenwijdig aan elkaar zijn.
- Alle zijden van de ruit zijn even lang, terwijl alleen de overstaande zijden van een parallellogram gelijk zijn.
- De diagonalen van een ruit snijden elkaar in de rechte hoeken en vormen zo twee schalene-driehoeken. In tegenstelling tot een parallellogram waarvan de diagonalen elkaar snijden en zo twee congruente driehoeken vormen.
- De wiskundige formule voor de oppervlakte van een ruit is (pq)/2, waarbij p en q de diagonalen zijn. Omgekeerd kan de oppervlakte van het parallellogram worden berekend door basis en hoogte te vermenigvuldigen.
- De omtrek van ruit kan worden berekend met behulp van de volgende formule – 4 a, waarbij a = zijde van de ruit. Daarentegen kan de omtrek van het parallellogram worden berekend door – basis en hoogte op te tellen, en de som met 2 te vermenigvuldigen.
Conclusie
Zowel een parallellogram als een ruit zijn vierhoeken, waarvan de tegenoverliggende zijden evenwijdig zijn, de tegenoverliggende hoeken gelijk zijn, de som van de binnenhoeken is 360 graden. Een ruit zelf is een speciaal soort parallellogram. Daarom kan men zeggen dat elke ruit een parallellogram is, maar het omgekeerde is niet mogelijk.