Onlangs stelde een collega van mij een aantal vragen zoals “waarom hebben we zoveel activeringsfuncties?”waarom werkt de ene beter dan de andere, hoe weten we welke we moeten gebruiken, is het hardcore wiskunde, enzovoort. Dus ik dacht, waarom schrijf ik er geen artikel over voor diegenen die slechts op een basisniveau bekend zijn met neurale netwerken en zich daarom afvragen hoe het zit met activeringsfuncties en hun “waarom-hoe-wiskunde!”.
NOOT: Dit artikel gaat ervan uit dat je een basiskennis hebt van een kunstmatig “neuron”. Ik raad u aan eerst de basisprincipes van neurale netwerken te bestuderen voordat u dit artikel leest voor een beter begrip.
Activeringsfuncties
Dus wat doet een kunstmatig neuron? Simpel gezegd berekent het een “gewogen som” van zijn input, voegt daar een bias aan toe en beslist dan of het moet worden “afgevuurd” of niet ( yeah right, een activeringsfunctie doet dit, maar laten we even met de stroom meegaan ).
Beschouw dus een neuron.
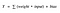
Nu, de waarde van Y kan van alles zijn, variërend van -inf tot +inf. Het neuron kent de grenzen van de waarde echt niet. Dus hoe beslissen we of het neuron moet vuren of niet (waarom dit vurenpatroon? Omdat we het uit de biologie hebben geleerd, dat is de manier waarop de hersenen werken en de hersenen zijn een werkend bewijs van een ontzagwekkend en intelligent systeem).
We hebben besloten om voor dit doel “activeringsfuncties” toe te voegen. Om de Y-waarde te controleren die door een neuron wordt geproduceerd en te beslissen of externe verbindingen dit neuron als “ontslagen” moeten beschouwen of niet. Of laten we zeggen – “geactiveerd” of niet.
Step functie
Het eerste wat in ons opkomt is wat te denken van een drempel-gebaseerde activeringsfunctie? Als de waarde van Y boven een bepaalde waarde ligt, wordt hij geactiveerd verklaard. Als het lager is dan de drempel, zeg je dat het niet zo is. Hmm geweldig. Dit zou kunnen werken!
Activeringsfunctie A = “geactiveerd” als Y > drempel anders niet
Alternatief, A = 1 als y> drempel, 0 anders
Wel, wat we net deden is een “stap functie”, zie de onderstaande figuur.
De uitgang ervan is 1 ( geactiveerd) als de waarde > 0 (drempel) is en geeft anders een 0 ( niet geactiveerd).
Geweldig. Dus dit maakt een activeringsfunctie voor een neuron. Geen verwarring. Er zijn echter bepaalde nadelen aan verbonden. Om het beter te begrijpen, denk aan het volgende.
Voorstel dat je een binaire classificator maakt. Iets dat een “ja” of “nee” moet zeggen ( activeren of niet activeren ). Een Step functie zou dat voor je kunnen doen! Dat is precies wat het doet, een 1 of 0 zeggen. Denk nu aan het gebruik waarbij je meerdere van zulke neuronen zou willen verbinden om meer klassen in te brengen. Klasse1, klasse2, klasse3 enz. Wat zal er gebeuren als meer dan 1 neuron wordt “geactiveerd”. Alle neuronen zullen een 1 uitvoeren (van de step-functie). Wat zou je nu beslissen? Welke klasse is het? Hmm moeilijk, ingewikkeld.
Je zou willen dat het netwerk slechts 1 neuron activeert en dat de anderen 0 zijn (alleen dan zou je kunnen zeggen dat het goed heeft geclassificeerd/ de klasse heeft geïdentificeerd). Ah! Dit is moeilijker te trainen en te convergeren op deze manier. Het zou beter zijn geweest als de activatie niet binair was en het in plaats daarvan zou zeggen “50% geactiveerd” of “20% geactiveerd” enzovoort. En als er dan meer dan 1 neuron activeert, zou je kunnen vinden welk neuron de “hoogste activatie” heeft enzovoort ( beter dan max, een softmax, maar dat laten we nu even achterwege ).
In dit geval ook, als er meer dan 1 neuron zegt “100% geactiveerd”, blijft het probleem nog steeds bestaan.Ik weet het! Maar..aangezien er intermediaire activeringswaarden voor de output zijn, kan het leren soepeler en gemakkelijker verlopen ( minder wiebelig ) en de kans dat meer dan 1 neuron 100% geactiveerd is, is kleiner in vergelijking met de stapfunctie tijdens het trainen ( ook afhankelijk van wat u traint en de gegevens ).
Ok, dus we willen iets om ons intermediaire ( analoge ) activeringswaarden te geven in plaats van te zeggen “geactiveerd” of niet ( binair ).
Het eerste wat in ons opkomt zou Lineaire functie zijn.
Lineaire functie
A = cx
Een rechte lijn functie waarbij de activering evenredig is met de input ( dat is de gewogen som van neuron ).
Op deze manier geeft het een bereik van activeringen, dus het is geen binaire activering. We kunnen zeker een paar neuronen met elkaar verbinden en als er meer dan 1 vuurt, kunnen we de max ( of softmax) nemen en op basis daarvan beslissen. Dus dat is ook ok. Wat is dan het probleem hiermee?
Als je bekend bent met gradient descent voor training, zou je merken dat voor deze functie, de afgeleide een constante is.
A = cx, afgeleide ten opzichte van x is c. Dat betekent, de gradient heeft geen relatie met X. Het is een constante gradient en de afdaling zal op constante gradient zijn. Als er een fout in de voorspelling zit, zijn de veranderingen die door back propagation worden gemaakt constant en niet afhankelijk van de verandering in input delta(x) !!!
Dit is niet zo goed! ( niet altijd, maar houd vol ). Er is ook nog een ander probleem. Denk aan geschakelde lagen. Elke laag wordt geactiveerd door een lineaire functie. Die activering gaat op zijn beurt naar het volgende niveau als input en de tweede laag berekent gewogen som op die input en die vuurt op zijn beurt weer op basis van een andere lineaire activeringsfunctie.
Hoe veel lagen we ook hebben, als ze allemaal lineair van aard zijn, is de uiteindelijke activeringsfunctie van de laatste laag niets anders dan gewoon een lineaire functie van de input van de eerste laag! Pauzeer even en denk er over na.
Dat betekent dat deze twee lagen ( of N lagen ) vervangen kunnen worden door één enkele laag. Ah! We hebben net de mogelijkheid verloren om op deze manier lagen te stapelen. Het maakt niet uit hoe we stapelen, het hele netwerk is nog steeds gelijk aan een enkele laag met lineaire activering ( een combinatie van lineaire functies op een lineaire manier is nog steeds een andere lineaire functie ).
Laten we verder gaan, zullen we?
Sigmoïde functie
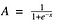
Wel, dit ziet er glad en “stapfunctie-achtig” uit. Wat zijn hier de voordelen van? Denk er eens even over na. Ten eerste is deze functie niet-lineair van aard. Combinaties van deze functie zijn ook niet-lineair! Geweldig. Nu kunnen we lagen stapelen. Hoe zit het met niet binaire activeringen? Ja, dat ook! Het zal een analoge activering geven in tegenstelling tot stap-functie. Het heeft ook een vloeiende gradiënt.
En als je ziet, tussen X waarden -2 tot 2, zijn Y waarden erg steil. Dat betekent dat kleine veranderingen in de waarden van X in dat gebied, de waarden van Y sterk doen veranderen. Ah, dat betekent dat deze functie de neiging heeft de Y-waarden naar beide uiteinden van de curve te brengen.
Het ziet er naar uit dat het goed is voor een classificator gezien zijn eigenschap? Ja, dat is het inderdaad. Het heeft de neiging de activeringen naar beide kanten van de curve te brengen ( boven x = 2 en onder x = -2 bijvoorbeeld). Een ander voordeel van deze activeringsfunctie is dat, in tegenstelling tot de lineaire functie, de output van de activeringsfunctie altijd in het bereik (0,1) zal liggen, in vergelijking met (-inf, inf) van de lineaire functie. Dus we hebben onze activeringen gebonden in een bereik. Mooi, dan worden de activeringen niet opgeblazen.
Dit is geweldig. Sigmoid functies zijn een van de meest gebruikte activeringsfuncties vandaag de dag. Wat zijn dan de problemen?
Als je kijkt, naar de uiteinden van de sigmoïde functie, reageren de Y waarden minder op veranderingen in X. Wat betekent dat? De gradiënt in dat gebied zal klein zijn. Het geeft aanleiding tot een probleem van “verdwijnende gradiënten”. Hmm. Dus wat gebeurt er als de activeringen in de buurt komen van het “bijna-horizontale” deel van de curve aan beide zijden?
Gradient is klein of verdwenen (kan geen significante verandering maken vanwege de extreem kleine waarde). Het netwerk weigert om verder te leren of is drastisch traag (afhankelijk van het gebruik en totdat de gradiënt / berekening wordt geraakt door floating point waarde limieten). Er zijn manieren om dit probleem te omzeilen en sigmoid is nog steeds erg populair in classificatie problemen.
Tanh Functie
Een andere activeringsfunctie die wordt gebruikt is de tanh functie.
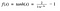
Hm. Dit lijkt erg op sigmoid. In feite is het een geschaalde sigmoïdefunctie!

Ok, nu heeft dit kenmerken die lijken op sigmoïde die we hierboven hebben besproken. Het is niet-lineair van aard, zo groot dat we lagen kunnen stapelen! Het is gebonden aan een bereik (-1, 1), dus geen zorgen over opgeblazen activeringen. Een punt om te vermelden is dat de gradiënt sterker is voor tanh dan voor sigmoid (de afgeleiden zijn steiler). De keuze tussen sigmoid of tanh hangt af van de vereiste sterkte van de gradiënt. Net als sigmoid, heeft tanh ook het verdwijnende gradient probleem.
Tanh is ook een zeer populaire en veel gebruikte activeringsfunctie.
ReLu
Later, komt de ReLu functie,
A(x) = max(0,x)
De ReLu functie is zoals hierboven getoond. Het geeft een uitvoer x als x positief is en anders 0.
Op het eerste gezicht lijkt dit dezelfde problemen te hebben als een lineaire functie, omdat deze lineair is in de positieve as. Allereerst is ReLu niet-lineair van aard. En combinaties van ReLu zijn ook niet lineair! ( in feite is het een goede benadering. Elke functie kan benaderd worden met combinaties van ReLu). Geweldig, dus dit betekent dat we lagen kunnen stapelen. Het is echter niet begrensd. Het bereik van ReLu is [0, inf). Dit betekent dat het de activering kan opblazen.
Een ander punt dat ik hier zou willen bespreken is de spaarzaamheid van de activering. Stel je een groot neuraal netwerk voor met heel veel neuronen. Als je een sigmoïde of tanh gebruikt, zullen bijna alle neuronen op een analoge manier vuren (weet je nog?). Dat betekent dat bijna alle activaties zullen worden verwerkt om de output van een netwerk te beschrijven. Met andere woorden, de activatie is dicht. Dit is kostbaar. Idealiter zouden we willen dat een paar neuronen in het netwerk niet geactiveerd worden, waardoor de activeringen spaarzaam en efficiënt worden.
ReLu geeft ons dit voordeel. Stel je een netwerk voor met willekeurig geïnitialiseerde gewichten ( of genormaliseerd ) en bijna 50% van het netwerk geeft 0 activering vanwege de karakteristiek van ReLu ( output 0 voor negatieve waarden van x ). Dit betekent dat er minder neuronen vuren ( sparse activatie ) en het netwerk lichter is. Woah, leuk! ReLu lijkt geweldig te zijn! Ja dat is het, maar niets is foutloos… Zelfs ReLu niet.
Omwille van de horizontale lijn in ReLu ( voor negatieve X ), kan de gradient naar 0 gaan. Voor activaties in dat gebied van ReLu, zal de gradient 0 zijn, waardoor de gewichten niet worden aangepast tijdens de afdaling. Dat betekent dat de neuronen die in die toestand komen, stoppen met reageren op variaties in de fout/input ( gewoon omdat de gradiënt 0 is, verandert er niets). Dit wordt het stervende ReLu probleem genoemd. Dit probleem kan ertoe leiden dat verschillende neuronen gewoon sterven en niet meer reageren, waardoor een aanzienlijk deel van het netwerk passief wordt. Er zijn variaties in ReLu om dit probleem op te lossen door simpelweg van de horizontale lijn een niet-horizontale component te maken. bijvoorbeeld y = 0.01x voor x<0 maakt er een licht hellende lijn van in plaats van een horizontale lijn. Dit is lekke ReLu. Er zijn ook andere variaties. Het belangrijkste idee is om de gradiënt niet nul te laten zijn en uiteindelijk tijdens de training te herstellen.
ReLu is minder rekenintensief dan tanh en sigmoid omdat er eenvoudiger wiskundige bewerkingen mee gemoeid zijn. Dat is een goed punt om te overwegen als we diepe neurale netten ontwerpen.
Ok, welke gebruiken we nu?
Nu, welke activeringsfuncties moeten we gebruiken. Betekent dat dat we gewoon ReLu gebruiken voor alles wat we doen? Of sigmoid of tanh? Nou, ja en nee. Als je weet dat de functie die je probeert te benaderen bepaalde kenmerken heeft, kun je een activeringsfunctie kiezen die de functie sneller benadert, wat leidt tot een sneller trainingsproces. Bijvoorbeeld, een sigmoïde werkt goed voor een classificator (zie de grafiek van sigmoïde, toont het niet de eigenschappen van een ideale classificator? ) omdat het benaderen van een classificatiefunctie als combinaties van sigmoïden eenvoudiger is dan bijvoorbeeld ReLu. Wat zal leiden tot een sneller trainingsproces en convergentie. Je kunt ook je eigen aangepaste functies gebruiken! Als je de aard van de functie die je probeert te leren niet kent, dan zou ik misschien voorstellen om met ReLu te beginnen, en dan achteruit te werken. ReLu werkt meestal als een algemene benadering!
In dit artikel heb ik geprobeerd een paar activeringsfuncties te beschrijven die vaak gebruikt worden. Er zijn ook andere activeringsfuncties, maar het algemene idee blijft hetzelfde. Onderzoek naar betere activeringsfuncties is nog gaande. Ik hoop dat je het idee achter activeringsfuncties hebt begrepen, waarom ze worden gebruikt en hoe we beslissen welke we moeten gebruiken.