De Lotka-Volterra vergelijkingen beschrijven een ecologisch predator-prooi (of parasiet-gastheer) model dat aanneemt dat, voor een reeks vaste positieve constanten 
(de groeisnelheid van de prooi), 
(de snelheid waarmee de roofdieren de prooi vernietigen), 
(de sterfte van de roofdieren), en 
(de snelheid waarmee de roofdieren toenemen door de prooi te consumeren), de volgende voorwaarden gelden.
1. Een prooipopulatie 
neemt toe met een snelheid 
(evenredig met het aantal prooien) maar wordt tegelijkertijd vernietigd door roofdieren met een snelheid 
(evenredig met het product van het aantal prooien en het aantal roofdieren).
2. Een roofdierenpopulatie 
neemt af met een snelheid 
(evenredig met het aantal roofdieren), maar neemt toe met een snelheid 
(weer evenredig met het product van het aantal prooien en het aantal roofdieren).
Dit levert de gekoppelde differentiaalvergelijkingen
 |
 |
 |
(1)
|
 |
 |
 |
(2)
|
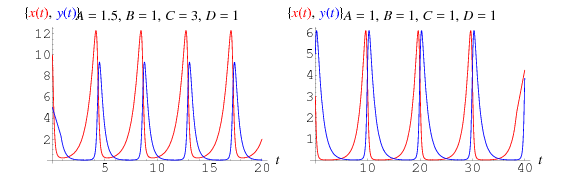
waarvan de oplossingen hierboven zijn geplot, waarbij de prooien in rood zijn weergegeven, en de roofdieren in blauw. In een dergelijk model ligt de curve van de prooi altijd voor op die van de predator.
Kritieke punten treden op wanneer 
, dus
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
Het enige stationaire punt bevindt zich dus op 
.