Inleidende bedrijfsstatistieken

Bekijk de volgende gegevensverzameling eens.
4; 5; 6; 6; 7; 7; 7; 7; 8; 8; 8; 9; 10

Deze gegevensverzameling kan worden weergegeven door het volgende histogram. Elk interval heeft breedte één, en elke waarde bevindt zich in het midden van een interval.

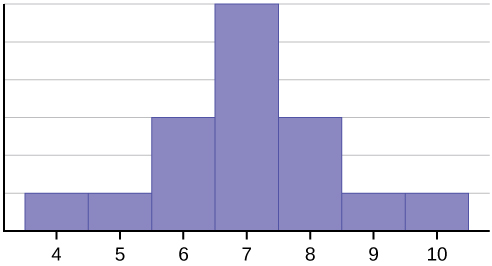
Het histogram geeft een symmetrische verdeling van gegevens weer. Een verdeling is symmetrisch als op een bepaald punt in het histogram een verticale lijn kan worden getrokken, zodanig dat de vorm links en rechts van de verticale lijn spiegelbeelden van elkaar zijn. Het gemiddelde, de mediaan en de modus zijn elk zeven voor deze gegevens. Bij een perfect symmetrische verdeling zijn het gemiddelde en de mediaan gelijk. Dit voorbeeld heeft één modus (unimodaal), en de modus is gelijk aan het gemiddelde en de mediaan. Bij een symmetrische verdeling met twee modi (bimodaal) zouden de twee modi verschillend zijn van het gemiddelde en de mediaan.

Het histogram voor de gegevens: 4566677778 is niet symmetrisch. De rechterkant lijkt “afgehakt” vergeleken met de linkerkant. Een dergelijke verdeling wordt scheef naar links genoemd omdat ze naar links wordt getrokken. We kunnen de scheefheid van een verdeling formeel meten, net zoals we mathematisch het middengewicht van de gegevens of de algemene “speadness” ervan kunnen meten. De wiskundige formule voor scheefheid is: . Hoe groter de afwijking van nul, hoe groter de mate van scheefheid. Als de scheefheid negatief is, is de verdeling naar links scheefgetrokken, zoals in (figuur). Een positieve maat voor de scheefheid wijst op een rechtse scheefheid, zoals in (Figuur).

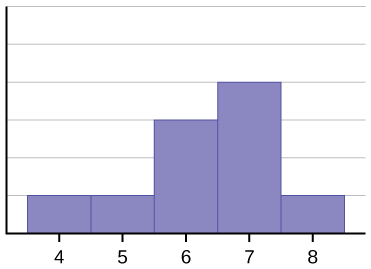
Het gemiddelde is 6,3, de mediaan is 6,5, en de modus is zeven. Merk op dat het gemiddelde kleiner is dan de mediaan, en dat ze allebei kleiner zijn dan de modus. Het gemiddelde en de mediaan geven beide de scheefheid weer, maar het gemiddelde meer.

Het histogram voor de gegevens: 67777888910, is ook niet symmetrisch. Het is scheef naar rechts.

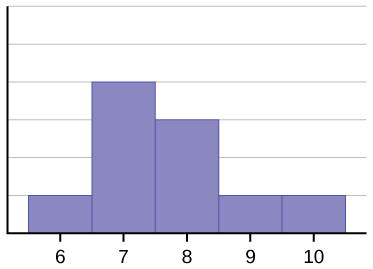
Het gemiddelde is 7,7, de mediaan is 7,5, en de modus is zeven. Van de drie statistieken is het gemiddelde het grootst, terwijl de modus het kleinst is. Ook hier weerspiegelt het gemiddelde de scheefheid het meest.

Om samen te vatten: als de verdeling van de gegevens naar links scheef is, is het gemiddelde over het algemeen kleiner dan de mediaan, die vaak kleiner is dan de modus. Als de verdeling van de gegevens naar rechts scheef is, is de modus vaak kleiner dan de mediaan, die weer kleiner is dan het gemiddelde.

Zoals voor het gemiddelde, de mediaan en de modus, en zoals we zo dadelijk zullen zien, de variantie, bestaan er wiskundige formules die ons precieze maatstaven geven voor deze kenmerken van de verdeling van de gegevens. Nogmaals kijkend naar de formule voor scheefheid zien we dat dit een relatie is tussen het gemiddelde van de gegevens en de individuele waarnemingen bij elkaar opgeteld.

waar de steekproefstandaardafwijking van de gegevens is, , en het rekenkundig gemiddelde en de steekproefgrootte.

Het rekenkundig gemiddelde staat bekend als het eerste moment van de verdeling. Het tweede moment is de variantie, en de scheefheid is het derde moment. De variantie meet de gekwadrateerde verschillen van de gegevens ten opzichte van het gemiddelde en de scheefheid meet de gekubde verschillen van de gegevens ten opzichte van het gemiddelde. Terwijl de variantie nooit negatief kan zijn, kan de scheefheid wel negatief zijn en zo bepalen we of de gegevens rechts of links scheef zijn. De scheefheid voor een normale verdeling is nul, en alle symmetrische gegevens zouden een scheefheid in de buurt van nul moeten hebben. Negatieve waarden voor de scheefheid wijzen op gegevens die naar links zijn gekeerd en positieve waarden voor de scheefheid wijzen op gegevens die naar rechts zijn gekeerd. Met scheefgetrokken links bedoelen we dat de linkerstaart lang is ten opzichte van de rechterstaart. Evenzo betekent scheef rechts dat de rechter staart lang is ten opzichte van de linker staart. De scheefheid karakteriseert de mate van asymmetrie van een verdeling rond het gemiddelde. Terwijl het gemiddelde en de standaardafwijking dimensionale grootheden zijn (daarom nemen wij de vierkantswortel van de variantie), d.w.z. dezelfde eenheden hebben als de gemeten grootheden , wordt de scheefheid conventioneel gedefinieerd op een wijze waardoor zij niet-dimensionaal is. Het is een zuiver getal dat alleen de vorm van de verdeling karakteriseert. Een positieve waarde van de scheefheid wijst op een verdeling met een asymmetrische staart die zich uitstrekt naar een positievere X en een negatieve waarde wijst op een verdeling waarvan de staart zich uitstrekt naar een negatievere X. Een scheefheid van nul wijst op een symmetrische verdeling.

Scheefheid en symmetrie worden belangrijk wanneer we in latere hoofdstukken kansverdelingen bespreken.