Het Toom-Cook Algoritme
Hier leren we een ingenieuze toepassing van een verdeel-en-heers algoritme gecombineerd met lineaire algebra om snel grote getallen te vermenigvuldigen. En een introductie tot de Big-O notatie!
In feite is dit resultaat zo contra-intuïtief dat de grote wiskundige Kolmogorov vermoedde dat zo’n snel algoritme niet bestond.
Deel 0: Lang vermenigvuldigen is langzaam vermenigvuldigen. (En een inleiding tot Big-O Notatie)
We weten allemaal nog dat we op school leerden vermenigvuldigen. Sterker nog, ik moet iets bekennen. Denk eraan, dit is een niet-veroordelende zone 😉
Op school hadden we ‘nat spelen’ als het te hard regende om op de speelplaats te spelen. Terwijl andere (normale/leuke/positieve-bijvoeglijk naamwoord-keuze) kinderen spelletjes deden en rommelden, pakte ik soms een vel papier en vermenigvuldigde grote getallen met elkaar, gewoon voor de lol. Het pure plezier van rekenen! We hadden zelfs een vermenigvuldigingswedstrijd, de ‘Super 144’, waarbij we een door elkaar gehusseld rooster van 12 bij 12 getallen (van 1 tot 12) zo snel mogelijk moesten vermenigvuldigen. Ik oefende dit religieus, in die mate dat ik mijn eigen vooraf voorbereide oefenbladen had, die ik fotokopieerde en dan bij toerbeurt gebruikte. Uiteindelijk kreeg ik mijn tijd terug tot 2 minuten en 1 seconde, waarbij mijn fysieke limiet van krabbelen was bereikt.
Ondanks deze obsessie met vermenigvuldigen, is het nooit bij me opgekomen dat we het beter konden doen. Ik heb zoveel uren besteed aan vermenigvuldigen, maar ik heb nooit geprobeerd het algoritme te verbeteren.
Neem eens 103 met 222.
We berekenen 2 maal 3 maal 1 +2 maal 0 maal 10 + 2 maal 1 maal 100 + 20 maal 3 maal 1 + 20 maal 0 maal 10 + 20 maal 1 maal 100 = 22800
In het algemeen zijn er voor het vermenigvuldigen met getallen van n cijfers O(n²) bewerkingen nodig. De ‘grote-O’-notatie betekent dat, als we het aantal bewerkingen als functie van n in een grafiek zouden zetten, het in feite om de term n² gaat. De vorm is in wezen kwadratisch.
Vandaag zullen we al onze kinderdromen vervullen en dit algoritme verbeteren. Maar eerst! Big-O wacht op ons.
Big-O
Kijk eens naar de twee grafieken hieronder

Vraag een wiskundige: “zijn x² en x²+x^(1/3) hetzelfde?”, en hij zal waarschijnlijk in zijn koffiekopje overgeven en beginnen te huilen, en iets mompelen over topologie. Tenminste, dat was mijn reactie (in het begin), en ik weet nauwelijks iets van topologie.
Ok. Ze zijn niet hetzelfde. Maar onze computer geeft niets om topologie. Computers verschillen in prestaties op zoveel manieren dat ik ze niet eens kan beschrijven omdat ik niets van computers weet.
Maar het heeft geen zin om een stoomwals te finetunen. Als twee functies, voor grote waarden van hun invoer, in dezelfde orde van grootte groeien, dan bevat dat voor praktische doeleinden de meeste relevante informatie.
In de grafiek hierboven zien we dat de twee functies voor grote invoer vrij gelijkaardig lijken. Maar ook x² en 2x² lijken op elkaar – de laatste is slechts tweemaal zo groot als de eerste. Bij x = 100 is de ene 10.000 en de andere 20.000. Dat betekent dat als we de ene kunnen berekenen, we waarschijnlijk ook de andere kunnen berekenen. Terwijl een functie die exponentieel groeit, zeg 10^x, bij x = 100 al veel groter is dan het aantal atomen in het heelal. (10¹⁰⁰ >>>> 10⁸⁰ wat een schatting is, het Eddington getal, op het aantal atomen in het universum volgens mijn Googlen*).
*inderdaad, ik gebruikte DuckDuckGo.
Het schrijven van gehele getallen als veeltermen is zowel heel natuurlijk als heel onnatuurlijk. 1342 = 1000 + 300 + 40 + 2 is heel natuurlijk. Schrijven 1342 = x³+3x²+4x + 2, waarbij x = 10, is enigszins vreemd.
In het algemeen, stel dat we twee grote getallen willen vermenigvuldigen, geschreven in basis b, met n cijfers per stuk. We schrijven elk getal van n cijfers als een polynoom. Als we het getal van n cijfers in r stukken splitsen, heeft dit veeltermgetal n/r termen.
Bijvoorbeeld, stel b = 10, r = 3, en ons getal is 142.122.912
We kunnen dit omzetten in
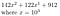
Dit werkt heel mooi als r = 3 en ons getal, geschreven in basis 10, 9 cijfers had. Als r n niet perfect deelt, dan kunnen we gewoon wat nullen vooraan toevoegen. Ook dit wordt het best geïllustreerd met een voorbeeld.
27134 = 27134 + 0*10⁵ = 027134, dat we voorstellen als
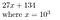
Waarom kan dit nuttig zijn? Om de coëfficiënten van de polynoom P te vinden, als de polynoom orde N heeft, kunnen we de coëfficiënten bepalen door hem op N+1 punten te bemonsteren.
Bijvoorbeeld, als de veelterm x⁵ + 3x³ +4x-2, die orde 5 is, op 6 punten wordt bemonsterd, dan kunnen we de gehele veelterm uitrekenen.
Intuïtief heeft een veelterm van orde 5 6 coëfficiënten: de coëfficiënt van 1, x, x², x³, x⁴, x⁵. Gegeven 6 waarden en 6 onbekenden, kunnen we de waarden achterhalen.
(Als je lineaire algebra kent, kun je de verschillende machten van x behandelen als lineair onafhankelijke vectoren, een matrix maken om de informatie weer te geven, de matrix inverteren, en voila)
Bemonstering van veeltermen om coëfficiënten te bepalen (Optioneel)
Hier gaan we wat dieper in op de logica achter het bemonsteren van een veelterm om de coëfficiënten af te leiden. Voel je vrij om naar de volgende sectie te gaan.
Wat we zullen laten zien is dat, als twee veeltermen van graad N overeenkomen op N+1 punten, dan moeten ze hetzelfde zijn. Dat wil zeggen dat N+1 punten een polynoom van orde N uniek specificeren.
Beschouw een polynoom van orde 2. Deze heeft de vorm P(z) = az² +bz + c. Door de fundamentele stelling van de algebra – schaamteloze plug hier, ik ben maanden bezig geweest om er een bewijs van te maken, en het vervolgens hier op te schrijven – kan deze polynoom in factoren worden ontbonden. Dat betekent dat we het kunnen schrijven als A(z-r)(z-w)
Merk op dat bij z = r, en bij z = w, de polynoom evalueert naar 0. We zeggen dat w en r wortels zijn van de polynoom.
Nu tonen we aan dat P(z) niet meer dan twee wortels kan hebben. Stel dat hij drie wortels heeft, die we w, r, s noemen. We ontbinden de polynoom dan in factoren. P(z) = A(z-r)(z-w). Dan is P(s) = A(s-r)(s-w). Dit is niet gelijk aan 0, want vermenigvuldiging van niet-nul getallen geeft een niet-nul getal. Dit is een tegenspraak omdat onze oorspronkelijke aanname was dat s een wortel was van de veelterm P.
Dit argument kan op een in wezen identieke manier worden toegepast op een veelterm van orde N.
Nu, stel dat twee veeltermen P en Q van orde N het eens zijn op N+1 punten. Als ze dan verschillend zijn, is P-Q een veelterm van orde N die op N+1 punten 0 is. Volgens het voorgaande is dit onmogelijk, want een veelterm van orde N heeft ten hoogste N wortels. Onze aanname moet dus fout zijn geweest, en als P en Q op N+1 punten overeenkomen zijn ze dezelfde veelterm.
Zien is geloven: A Worked Example
Laten we eens kijken naar een echt enorm getal dat we p noemen. In basis 10 is p 24 cijfers lang (n=24), en we zullen het in 4 stukken splitsen (r=4). n/r = 24/4 = 6
p = 292.103.243.859.143.157.364.152.
En laat de veelterm die dit voorstelt P heten,
P(x) = 292,103 x³ + 243,859 x² + 143,157 x+ 364,152
met P(10⁶) = p.
Omdat de graad van deze veelterm 3 is, kunnen we alle coëfficiënten uitwerken door op 4 plaatsen te bemonsteren. Laten we eens voelen wat er gebeurt als we het op een paar punten bemonsteren.
- P(0) = 364.152
- P(1) = 1.043.271
- P(-1) = 172.751
- P(2) = 3.962.726
Het opvallende is dat deze allemaal 6 of 7 cijfers hebben. Dat is vergeleken met de 24 cijfers die oorspronkelijk in p zaten.
Laten we p vermenigvuldigen met q. Stel q = 124,153,913,241,143,634,899,130, en
Q(x) = 124,153 x³ + 913,241 x²+143,634 x + 899,130
Het uitrekenen van t=pq zou afschuwelijk kunnen zijn. Maar in plaats van het rechtstreeks te doen, proberen we de veeltermvoorstelling van t te berekenen, die we bestempelen als T. Daar P een veelterm is van orde r-1=3, en Q een veelterm van orde r-1 = 3, is T een veelterm van orde 2r-2 = 6.
T(10⁶) = t = pq
T(10⁶) = P(10⁶)Q(10⁶)
De truc is dat we de coëfficiënten van T gaan uitrekenen, in plaats van p en q direct met elkaar te vermenigvuldigen. Dan is het berekenen van T(1⁰⁶) eenvoudig, want om te vermenigvuldigen met 1⁰⁶ plakken we gewoon 6 nullen achteraan. Alle delen optellen is ook gemakkelijk, want optellen is een zeer goedkope handeling voor computers om te doen.
Om de coëfficiënten van T te berekenen, moeten we hem bemonsteren op 2r-1 = 7 punten, want het is een polynoom van orde 6. We willen waarschijnlijk kleine gehele getallen kiezen, dus kiezen we
- T(0)=P(0)Q(0)= 364.152*899.130
- T(1)=P(1)Q(1)= 1.043.271*2.080.158
- T(2)=P(2)Q(2)= 3.962.726*5.832,586
- T(-1)=P(-1)Q(-1)= 172751*1544584
- T(-2)=P(-2)Q(-2)= -1.283.550*3.271,602
- T(3)=P(-3)Q(-3)= -5.757.369*5.335.266
Noteer de grootte van P(-3), Q(-3), P(2), Q(2) etc… Dit zijn allemaal getallen met ongeveer n/r = 24/4 = 6 cijfers. Sommige zijn 6 cijfers, sommige zijn 7 cijfers. Naarmate n groter wordt, wordt deze benadering steeds redelijker.
Tot nu toe hebben we het probleem teruggebracht tot de volgende stappen, of algoritme:
(1) Bereken eerst P(0), Q(0), P(1), Q(1), etc (goedkope actie)
(2) Om onze 2r-1= 7 waarden van T(x) te krijgen, moeten we nu 2r-1 getallen van benaderende grootte n/r cijfers lang vermenigvuldigen. We moeten namelijk P(0)Q(0), P(1)Q(1), P(-1)Q(-1), enz. berekenen. (Hoge kosten actie)
(3) Reconstrueer T(x) uit onze datapunten. (Lage kosten actie: maar komt later aan de orde).
(4) Met onze gereconstrueerde T(x), evalueer T(10⁶) in dit geval
Dit leidt mooi tot een analyse van de draaitijd van deze aanpak.
Looptijd
Uit het bovenstaande hebben we afgeleid dat, als we de handelingen met lage kosten (1) en (3) tijdelijk buiten beschouwing laten, de kosten van het vermenigvuldigen van twee n-cijferige getallen met het algoritme van Toom als volgt zullen zijn:
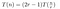
Dit is wat we in het uitgewerkte voorbeeld hebben gezien. Het vermenigvuldigen van P(0)Q(0), P(1)Q(1), enz kost T(n/r) omdat we twee getallen van lengte ongeveer n/r vermenigvuldigen. We moeten dit 2r-1 keer doen, want we willen T(x) – zijnde een veelterm van orde 2r-2 – op 2r-1 plaatsen bemonsteren.
Hoe snel is dit? We kunnen dit soort vergelijkingen expliciet oplossen.

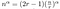
Het enige wat nu overblijft is wat rommelige algebra
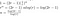
Omdat er nog wat andere kosten waren van het matrixvermenigvuldigingsproces (‘opnieuw in elkaar zetten’), en van de optelling, kunnen we niet echt zeggen dat onze oplossing de exacte runtime is, dus concluderen we in plaats daarvan dat we de big-O van de runtime hebben gevonden
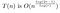
Optimaliseren van r
Deze runtime hangt nog steeds af van r. Repareer r, en we zijn klaar. Maar onze nieuwsgierigheid is nog niet bevredigd!
Als n groot wordt, willen we een ongeveer optimale waarde vinden voor onze keuze van r. Dat wil zeggen dat we een waarde van r willen kiezen die verandert voor verschillende waarden van n.
Het belangrijkste hier is dat we, met r variërend, enige aandacht moeten besteden aan de hermontagekosten – de matrix die deze operatie uitvoert heeft een kostprijs van O(r²). Toen r vast was, hoefden we daar niet naar te kijken, want toen n groter werd met r vast, waren het de termen waarbij n betrokken was die de groei bepaalden van hoeveel rekenwerk er nodig was. Aangezien onze optimale keuze van r groter zal worden naarmate n groter wordt, kunnen we dit niet langer negeren.
Dit onderscheid is cruciaal. Aanvankelijk koos onze analyse een waarde van r, misschien 3, misschien 3 miljard, en keek dan naar de big-O grootte als n willekeurig groot werd. Nu kijken we naar het gedrag als n willekeurig groot wordt en r groeit met n mee met een door ons te bepalen snelheid. Deze verandering van perspectief beschouwt O(r²) als een variabele, terwijl toen r vast werd gehouden, O(r²) een constante was, zij het een die we niet kenden.
Dus updaten we onze analyse van voorheen:
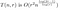
waar de O(r²) de kosten van de hermontagematrix voorstelt. We willen nu voor elke waarde van n een waarde van r kiezen, die deze uitdrukking bij benadering minimaliseert. Om te minimaliseren proberen we eerst te differentiëren ten opzichte van r. Dit geeft de ietwat afschuwelijk uitziende uitdrukking

Normaal gezien stellen we, om het minimumpunt te vinden, de afgeleide gelijk aan 0. Maar deze uitdrukking heeft geen mooi minimum. In plaats daarvan zoeken we een ‘goed genoeg’ oplossing. We gebruiken r = r^(sqrt(logN)) als onze geschatte waarde. Grafisch is dit vrij dicht bij het minimum. (In de grafiek hieronder is de factor 1/1000 er om de grafiek op redelijke schaal zichtbaar te maken)
De grafiek hieronder toont onze functie voor T(N), geschaald met een constante, in rood. De groene lijn is bij x = 2^sqrt(logN) wat onze geschatte waarde was. x’ neemt de plaats in van ‘r’, en in elk van de drie afbeeldingen wordt een andere waarde van N gebruikt.



Dit is voor mij behoorlijk overtuigend dat onze keuze een goede was. Met deze keuze van r, kunnen we het inpluggen en zien hoe ons algoritme uiteindelijk big-O:

waar we gewoon onze waarde voor r inplugden, en een benadering voor log(2r-1)/log(r) gebruikten die zeer accuraat is voor grote waarden van r.
Hoe groot is de verbetering?
Misschien was het redelijk dat ik dit algoritme niet opmerkte toen ik nog een kleine jongen was die vermenigvuldigde. In de grafiek hieronder geef ik de coëfficiënt van onze big-O functie 10 (ter demonstratie) en deel die door x² (omdat de oorspronkelijke aanpak van vermenigvuldigen O(n²) was). Als de rode lijn naar 0 neigt, zou dat laten zien dat onze nieuwe looptijd het asymptotisch beter doet dan O(n²).
En inderdaad, hoewel de vorm van de functie laat zien dat onze aanpak uiteindelijk sneller is, en uiteindelijk is hij veel sneller, moeten we wachten tot we bijna 400 cijfer lange getallen hebben om dit te laten zien! Zelfs als de coëfficiënt slechts 5 zou zijn, zouden de getallen ongeveer 50 cijfers lang moeten zijn om een snelheidsverbetering te zien.

Voor mijn 10 jaar oude zelf zou het vermenigvuldigen van getallen van 400 cijfers een beetje veel werk zijn! Het bijhouden van de verschillende recursieve aanroepen van mijn functie zou ook een beetje ontmoedigend zijn. Maar voor een computer die een taak in AI of natuurkunde uitvoert, is dit een veel voorkomend probleem!
Hoe diepgaand is dit resultaat?
Wat ik zo leuk vind aan deze techniek, is dat het geen raketwetenschap is. Het is niet de meest verbijsterende wiskunde die ooit ontdekt is. Achteraf lijkt het misschien voor de hand liggend. Toch is dit de briljantheid en schoonheid van wiskunde. Ik las dat Kolmogorov in een seminar vermoedde dat vermenigvuldiging fundamenteel O(n²) was. Kolmogorov heeft in principe veel van de moderne waarschijnlijkheidstheorie en analyse uitgevonden. Hij was een van de wiskundige grootheden van de 20e eeuw. Maar op dit ongerelateerde gebied bleek dat er een heel corpus van kennis lag te wachten om ontdekt te worden, recht onder zijn en andermans neus!
In feite komen Verdeel en heers algoritmen vandaag de dag vrij snel bij me op, omdat ze zo algemeen worden gebruikt. Maar zij zijn een product van de computerrevolutie, in die zin dat de menselijke geest zich pas met de enorme rekenkracht specifiek is gaan richten op de snelheid van het rekenen als een gebied van de wiskunde dat op zichzelf de moeite van het bestuderen waard is.
Daarom zijn wiskundigen niet zomaar bereid te accepteren dat de Riemann Hypothese waar is, alleen omdat het erop lijkt dat het waar zou kunnen zijn, of dat P niet gelijk is aan NP, alleen omdat dat het meest waarschijnlijk lijkt. De wondere wereld van de wiskunde behoudt altijd een vermogen om onze verwachtingen in de war te sturen.
In feite kun je nog snellere manieren vinden om te vermenigvuldigen. De huidige beste benaderingen gebruiken snelle fourier transformaties. Maar dat bewaar ik voor een andere dag 🙂
Laat me je gedachten hieronder weten. Ik ben nieuw op Twitter als ethan_the_mathmo, je kunt me hier volgen.
Ik kwam dit probleem tegen in een prachtig boek dat ik gebruik genaamd ‘The Nature of Computation’ van de natuurkundigen Moore en Mertens, waar een van de problemen je leidt door het analyseren van Toom’s algoritme.