Hoe help je leerlingen die moeite hebben met woordproblemen

“Ze kennen de wiskunde. Ze kunnen alleen de woordproblemen niet maken. Het is hun leesvaardigheid.”

Mw. Hartwell legde uit waarom haar leerlingen moeite hadden met de staatstoetsen. Ze kende haar studenten, en had voldoende beoordelingen gedaan. Ze was er zeker van dat hun problemen te maken hadden met lezen en schrijven.

“Ik begrijp niet waarom ze het lezen zo moeilijk maken. De kinderen doen al een taaltoets.”

Ik was aan mevrouw Hartwell (en anderen op haar school) gekoppeld als onderdeel van een New York City programma om de wiskundeprestaties te verbeteren. Het doel was om conceptuele wiskunde naar “Tier 1” scholen te brengen. Tier 1 scholen waren diegene die de stad aanvoerden op drie gebieden. Het laagste inkomen, de laagste testscores en het hoogste percentage gekleurde leerlingen.

Ik had de ‘geletterdheid’ uitleg gehoord van andere leraren in het programma. En het klonk logisch. Als de leerlingen de wiskunde kenden, waarom hadden ze het anders moeilijk op de toets, die veel woordproblemen bevatte?

Maar er zat een addertje onder het gras. In de afgelopen drie jaar, was de leesvaardigheid van 30%-40%, in de hele stad gestegen. In dezelfde periode zijn de scores voor wiskunde vrijwel gelijk gebleven.

Als dit een leesprobleem was, zou een stijging van de leesscores een explosieve groei in wiskunde moeten teweegbrengen. Bovendien leek de taal in de woordproblemen niet ingewikkeld genoeg om problemen te veroorzaken.

De volgende periode was ik ingepland om de klas van mevrouw Hartwell te bezoeken. Ze had een les over woordproblemen gepland, dus ik kon het probleem uit de eerste hand zien.

Over-Scaffolding Word Problems

De leerlingen zaten aan ronde tafels, en zij stond vooraan. Zij en haar leerlingen hadden allemaal een handheld whiteboard.

Ze openden hun tekstboek op bladzijde 47 en zij las een woordprobleem hardop voor. “Sarah heeft 40 pond wortels voor haar paarden. Als ze 100 paarden heeft, hoeveel pond krijgt elk paard dan?”

“OK klas, ze heeft 40 pond die ze aan elk paard zal geven. Dus welke operatie hebben we nodig?”

Ze wees op een ankergrafiek met de ‘sleutelwoorden’ voor elke bewerking. Elk’ stond bovenaan de delingslijst.

“Delen!” antwoordde de klas.

“Juist. Dus hoe delen we een klein getal door een groot getal?”

De klas was stil. Ms. Hartwell tekende een vinculum (huis voor lange delingen) op haar whiteboard. De leerlingen kopieerden terwijl ze 40 onder het huis zette en 100 erbuiten.

“Nu past 100 niet in 40, dus moeten we een decimaal toevoegen.” Ze veranderde 40 in 40,0. “Hoeveel keer gaat 100 in 400?”

Een paar leerlingen riepen: “Vier!”

“Precies. Nu moeten we ook nog een decimaal in ons quotiënt zetten. Ons uiteindelijke antwoord is?”

De klas las het antwoord, “0,4”, van haar whiteboard.

Ze gaf een soortgelijk probleem en wees op de “CUBES”-poster aan de muur. “Vergeet niet de getallen te omcirkelen en de sleutelwoorden in te vullen.’

Ze liep rond terwijl de leerlingen werkten. Sommigen vroegen waar ze de decimalen moesten zetten. Anderen hadden moeite met het aftrekken van de lange deling. Sommige leerlingen werkten in tweetallen, waarbij de een het rekenwerk deed, terwijl de ander kopieerde.

Aan het eind van de les had iedereen het juiste antwoord op zijn papier. “Zie je?” Ms. Hartwell merkte op, “ze kennen allemaal de wiskunde.”

What Went Wrong?

Hoewel dit een extreem voorbeeld is, zijn veel van de fouten die Ms. Hartwell maakte eigenlijk heel gewoon.

Over-scaffolding treedt op wanneer we leerlingen te veel ondersteuning geven. Terwijl het gebruikelijk is voor opvoeders om trots te zijn op het geven van leerlingen ‘zoveel steun als ze nodig hebben’, is over-scaffolding iets anders.

De term ‘scaffolding’ komt uit het werk van Lev Vygotsky. Hij bedacht de term “Zone van Proximale Ontwikkeling.” De ZPD omvat dingen die net buiten het bereik van een leerling liggen. Ze kunnen het niet helemaal alleen, maar ze kunnen het wel met ondersteuning. Door ‘steigers’ te plaatsen, kunnen we deze vaardigheden in de kernvaardigheden van een leerling plaatsen.

Wat vaak over het hoofd wordt gezien, is dat steigers alleen van toepassing zijn op vaardigheden die zich al in de ZPD van een leerling bevinden. Er zijn een hele reeks vaardigheden die momenteel buiten het bereik van een leerling liggen. Als we proberen deze vaardigheden te steigeren, doen we meer kwaad dan goed.

Eén probleem met over-scaffolding is dat leerlingen de beoogde vaardigheden nooit internaliseren. Als we een leerling helpen met iets dat buiten zijn ZPD ligt, zal hij altijd onze hulp nodig hebben. Tenminste totdat we de tussenliggende vaardigheden identificeren die wel in hun ZPD liggen.

Een ander probleem is dat over-scaffolding ons een vals gevoel van succes geeft. In dit geval dacht mevrouw Hartwell dat haar leerlingen konden ‘rekenen’ met het woordprobleem. In werkelijkheid deden ze alleen haar handelingen na. Er was geen reden om aan te nemen dat ze zelf een vergelijkbare oplossing konden vinden.

Ze verwijderde ook het hele proces van ‘formuleren’ uit het probleemoplossingsproces. Veel opvoeders zien begrip en formulering als hetzelfde, maar formulering is een aparte wiskundige competentie.

En het kan net het ontbrekende ingrediënt zijn in de manier waarop u momenteel woordproblemen onderwijst.

Classroom Resources and Professional Learning

Formulation: The Key to Success with Word Problems

Het formuleren van woordproblemen houdt in dat je ze begrijpt. Maar het gaat verder dan dat. Formuleren lijkt meer op vertalen dan op begrijpen.

Wanneer een leerling een woordprobleem leest, moet hij eerst letters omzetten in klanken (decoderen). Dan moeten ze begrijpen wat de woorden betekenen (vocabulaire). Ze moeten begrijpen hoe de woorden in elkaar passen in een zin (zinsbouw). Tot slot komt begrip voort uit het samenvoegen van deze stukjes tot een betekenis.

De meeste leerlingen uit de zesde klas kunnen het probleem van mevrouw Hartwell lezen en gemakkelijk begrijpen dat Sarah wortels uitdeelt aan haar paarden. Maar veel minder leerlingen zullen het “delen” van wortels met deling in verband brengen.

Dit is het deel waar veel docenten van balen. Het lijkt zo vanzelfsprekend voor ons. “Ze verdeelt letterlijk de wortels. Hoe kunnen ze niet zien dat het een verdeling is.”

Dat zien ze gewoon niet. Als dat zo was, zou je geen woordgrafieken zien hangen in de wiskundelokalen. En het gaat allemaal terug tot toen we voor het eerst bewerkingen leerden.

Waarom leerlingen moeite hebben met formuleren

Veel leraren op veel scholen leren leerlingen dat wiskunde een vak is van zingeving. Maar op andere scholen wordt wiskunde onderwezen als een vak van onthouden.

Een voorbeeld van ‘wiskunde als onthouden’ is wanneer leerlingen wiskundefeiten uit het hoofd leren. Maar algoritmen gaan ook over onthouden. Zet 120 boven op 47. Volg deze stappen om op te tellen, deze om af te trekken, en deze om te vermenigvuldigen.

Studenten kunnen deze stappen herhalen zonder te begrijpen hoe groot de getallen zijn of zelfs wat de bewerkingen betekenen.

Wanneer we beginnen met concepten (door visuele modellen of getalzinnen te gebruiken), leren studenten wat de bewerkingen betekenen. Wanneer we direct naar een algoritme gaan, denken leerlingen aan bewerkingen als een reeks willekeurige stappen.

Jaar na jaar laten we leerlingen onthouden en herhalen. Ze maken hetzelfde algoritme 30 keer voor huiswerk. Verander de getallen, en het proces blijft hetzelfde. Maar geef ze een woordprobleem, en nu moeten ze het begrijpen.

Wat de tests ons vertellen over redeneren

We kunnen onze leerlingen 10 problemen geven met de titel “Division Word Problems,” om het makkelijker te maken. Ze hoeven de problemen niet eens te lezen. Ze hoeven alleen maar uit te zoeken (of te raden) welk getal de deler is en welk getal de deling.

Maar als leerlingen een staatstoets maken, is het doel niet om het makkelijker te maken. Het doel is om te beoordelen wat ze zelf kunnen.

De toetsmakers willen hen niet vertellen welke bewerking ze moeten gebruiken. Ze zullen zelfs sleutelwoorden voor deling en optelling in dezelfde opgave zetten. “Er zitten 20 leerlingen in de klas. Als elk kind drie dollar heeft, hoeveel hebben ze dan in totaal?”

Dus als leerlingen moeite hebben met woordproblemen, gaat het niet alleen om de woordproblemen. Het betekent meestal dat ze wiskunde uit hun hoofd doen.

Studenten hebben strategieën en processen nodig om woordproblemen op te lossen

Een deel van het probleem met een systeem als CUBES is dat het zichzelf een strategie noemt, maar dat het eigenlijk een proces is.

Een proces is een reeks stappen. Als je eenmaal een efficiënt proces hebt gevonden, kun je het steeds herhalen zonder er al te veel bij na te denken. Algoritmen zijn een proces. Net als het op een rij zetten van ‘langste naar kortste’ voor de wandeling naar de lunch.

Een strategie is anders. Strategieën vereisen diepgaand inzicht. En het vermogen om begrip toe te passen in nieuwe situaties.

We kunnen leerlingen niet voorbereiden op elk scenario dat ze in een woordprobleem tegenkomen. Sommige vereisen dat ze verschillende wiskundige vaardigheden combineren die ze nog nooit hebben gecombineerd. Of ze kunnen vereisen dat leerlingen de volgorde van de stappen veranderen om tot de juiste oplossing te komen.

Bedenk het volgende:

Je hebt 5 liter sap voor een schoolfeest met 100 leerlingen. Als in elk bekertje 3 oz past, hoeveel bekertjes kan elke leerling dan drinken? Hoeveel blijft er over?

Een probleemoplossend proces kan leerlingen helpen dit probleem aan te pakken. “Stel vast wat er gevraagd wordt.” “Bedenk welke informatie wordt gegeven.”

Maar er is geen vast proces dat we ze kunnen leren om het daadwerkelijk op te lossen. Dat is waar strategie om de hoek komt kijken. Ze moeten eenheden omrekenen. Erkennen dat we delen met resten, in plaats van volledig te delen. Ze moeten waarschijnlijk ook de volgorde van de bewerkingen veranderen, door het sap eerst in bekers te verdelen en dan pas door het aantal leerlingen.

Er is geen “trucje” dat leerlingen zo ver krijgt. Ze moeten de betekenis van bewerkingen begrijpen. Ze moeten wiskunde begrijpen als een onderwerp van zingeving. En ze moeten herhaaldelijk oefenen in het toepassen van strategisch denken op woordproblemen.

Het Polya-proces voor het oplossen van woordproblemen

George Pólya was een invloedrijke Hongaarse wiskundige en Stanford-professor die een proces vond dat kon worden gebruikt om elk probleem op te lossen. Zijn werk heeft talloze wiskundigen en onderwijzers geraakt, van wie de meesten zijn naam niet kennen.

In feite zijn CUBES en andere zogenaamde probleemoplossingsstrategieën losjes gebaseerd op zijn werk. Het probleem is dat ze het proberen te vereenvoudigen. In het proces, verwijderen ze alles wat lijkt op diep denken.

Polya geloofde dat elk probleem in vier stappen kon worden opgelost: Begrijpen, Plannen, Oplossen, en Reflecteren. Ik denk dat Polya’s oorspronkelijke vier-stappen-proces prima geschikt is voor gebruik op scholen.

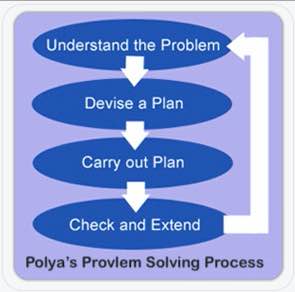Om het probleem te begrijpen, stellen we vast welke informatie wordt gegeven en wat we willen vinden. Dit is waar de ‘C’ en ‘U’ in blokjes vandaan komen. Als leerlingen de getallen willen omcirkelen en de vraag willen onderstrepen, prima. Ik heb liever dat ze ze (met eenheden) opschrijven in een grafisch schema, althans in het begin. Dit helpt hen te verwerken wat ze lezen. Het helpt mij ook, als leraar, om hun begrip te beoordelen terwijl ik door de kamer loop.

Volgende is het lastige deel. Het ‘plan’ is waar we het probleem formuleren. We nemen een scenario uit de echte wereld en zetten dat om in een wiskundige voorstelling.

De derde stap is het oplossen. Als we goed geformuleerd hebben, gaan we nu rekenen. Leerlingen gebruiken meestal een algoritme, maar ik moedig het gebruik van vergelijkingen en visuele modellen ook aan.

Ten slotte kijken leerlingen terug en controleren hun werk. Ze moeten ook nadenken over hun proces. Als ik een fout heb gemaakt, waarom? Zou deze strategie me kunnen helpen om in de toekomst soortgelijke problemen op te lossen?

Strategieën voor het oplossen van woordproblemen

Het hebben van een proces om woordproblemen te benaderen is zeker nuttig. Maar we kunnen niet doen alsof je betekenisvolle wiskunde leert door alleen maar stappen te volgen. Het hele punt van woordproblemen is om wiskunde uit te breiden voorbij “wiskundefeiten” en algoritmen.

Er zijn enkele nuttige strategieën om leerlingen te helpen met formuleren. In het begin leer ik expliciet een aantal verschillende strategieën.

Terwijl ik de strategieën aanleer, laat ik leerlingen problemen oplossen die goed bij die strategie passen. Sommige soorten problemen passen heel goed bij ‘Raden en controleren’. Andere zijn meer geschikt voor ‘Teken een plaatje’.

Eindelijk geef ik ze uitdagende woordproblemen die op verschillende manieren kunnen worden opgelost. Als ze de gereedschappen eenmaal in hun gereedschapsgordel hebben, kunnen ze kiezen welke het beste is voor de situatie.

Het combineren van strategieën kan ook heel effectief zijn. Het maken van een tekening kan bijvoorbeeld vaak helpen bij het formuleren. Als een boer 18 rijen wortels heeft met 10 wortels in elke rij, kan een leerling beginnen met het tekenen van het veld. Op een gegeven moment kunnen ze denken: “Wow, dit is een matrix”, en beseffen dat ze kunnen vermenigvuldigen met behulp van mentale wiskunde, een uitdrukking of een algoritme.

Andere keren kunnen leerlingen visuele modellen gebruiken om het probleem te formuleren en op te lossen.

Help uw leerlingen om uitdagende woordproblemen aan te pakken

Als u zoals veel leraren bent, maakt u zich misschien zorgen over hoe uw leerlingen dit allemaal zullen aanpakken. Processen, strategieën, kritisch denken… er komt heel wat bij kijken.

Misschien denkt u zelfs dat woordproblemen vóór dit artikel gemakkelijker leken. Als dat zo is, mijn excuses.

De sleutel is om niet overweldigd te raken door alles tegelijk te doen. Begin met het oplossen van een eenvoudig woordprobleem met behulp van Polya’s proces. Introduceer dan elke week een nieuwe strategie. Aan het eind van het jaar zult u verbaasd zijn over hoe ver ze zijn gekomen.

Misschien wilt u dieper ingaan op creatief problemen oplossen. Overweeg het volgen van een praktische wiskundeworkshop of het werken met een online coach.

Als u klaar bent om morgen Polya in de klas te brengen, is dit grafische schema een geweldige manier om te beginnen. Het zal het vier-stappen-proces ondersteunen en u helpen vast te stellen waar uw leerlingen ontsporen.

Free Word Problem Organizer

Over de auteur

Jeff Lisciandrello is de oprichter van Room to Discover en een onderwijsconsultant die zich specialiseert in student-gecentreerd leren. Zijn 3-Bridges Design for Learning helpt scholen bij het verkennen van innovatieve praktijken binnen traditionele omgevingen. Hij geniet van het helpen van docenten bij het omarmen van onderzoekende en gepersonaliseerde benaderingen van instructie. U kunt met hem in contact komen via Twitter @EdTechJeff