Posted on 29th November 2018 by Maximilian Siebert
Heterogeniteit is niet iets om bang voor te zijn, het betekent alleen dat er variabiliteit in je gegevens zit. Als men dus verschillende studies samenbrengt om ze te analyseren of een meta-analyse uit te voeren, is het duidelijk dat er verschillen zullen worden gevonden. Het tegenovergestelde van heterogeniteit is homogeniteit, wat betekent dat alle studies hetzelfde effect laten zien.
Het is belangrijk op te merken dat er verschillende soorten heterogeniteit zijn:
- Klinisch: Verschillen in deelnemers, interventies of uitkomsten
- Methodologisch: Verschillen in studieopzet, risico van bias
- Statistisch: Variatie in interventie-effecten of resultaten
We zijn geïnteresseerd in deze verschillen omdat ze erop kunnen wijzen dat onze interventie misschien niet elke keer dat deze wordt gebruikt op dezelfde manier werkt. Door deze verschillen te onderzoeken, kunt u tot een veel beter begrip komen van welke factoren van invloed zijn op de interventie, en welk resultaat u de volgende keer dat de interventie wordt toegepast, kunt verwachten.
Hoewel klinische en methodologische heterogeniteit belangrijk zijn, zal deze blog zich richten op statistische heterogeniteit.
Hoe heterogeniteit te identificeren en te meten
Eyeball test
Kijk in uw forest plot naar overlappende betrouwbaarheidsintervallen, en niet zozeer aan welke kant uw effectschattingen liggen. Of de resultaten aan weerszijden van de lijn van geen effect liggen, is misschien niet van invloed op uw beoordeling van de vraag of er sprake is van heterogeniteit, maar het kan wel van invloed zijn op uw beoordeling van de vraag of de heterogeniteit ertoe doet.
Met dit in gedachten bekijkt u de onderstaande grafiek en beslist u welke plot homogener is.
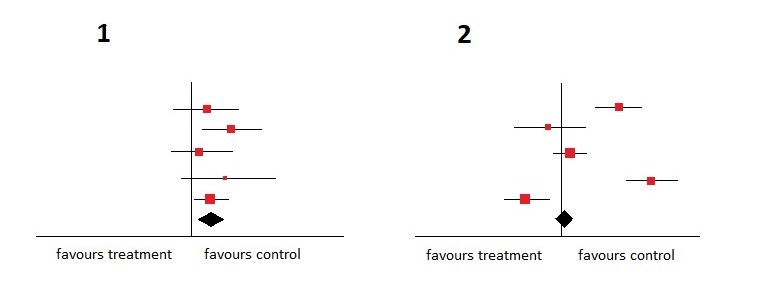
De homogenere plot is natuurlijk plot nummer 1 . De betrouwbaarheidsintervallen overlappen elkaar allemaal en bovendien geven alle studies de voorkeur aan de controle-interventie.
Voor de mensen die graag dingen meten in plaats van er alleen maar naar te kijken, geen zorgen, er zijn nog statistische methoden om u te helpen het concept van heterogeniteit te doorgronden.
Chi-kwadraat (χ²)-test
Deze test gaat uit van de nulhypothese dat alle studies homogeen zijn, of dat elke studie een identiek effect meet, en geeft ons een p-waarde om deze hypothese te testen. Als de p-waarde van de test laag is, kunnen we de hypothese verwerpen en is er sprake van heterogeniteit.
Omdat de test vaak niet gevoelig genoeg is en het ten onrechte uitsluiten van heterogeniteit snel gebeurt, gebruiken veel wetenschappers een p-waarde van < 0,1 in plaats van < 0,05 als afkapwaarde.
I²
Deze test is ontwikkeld door professor Julian Higgins en heeft een theorie om de mate van heterogeniteit te meten in plaats van aan te geven of deze al dan niet aanwezig is.
Drempels voor de interpretatie van I² kunnen misleidend zijn, omdat het belang van inconsistentie van verschillende factoren afhangt. Een ruwe leidraad voor de interpretatie is als volgt:
- 0% tot 40%: misschien niet belangrijk
- 30% tot 60%: matige heterogeniteit
- 50% tot 90%: substantiële heterogeniteit
- 75% tot 100%: aanzienlijke heterogeniteit
Om bovenstaande theorie te begrijpen, bekijk het volgende voorbeeld eens.
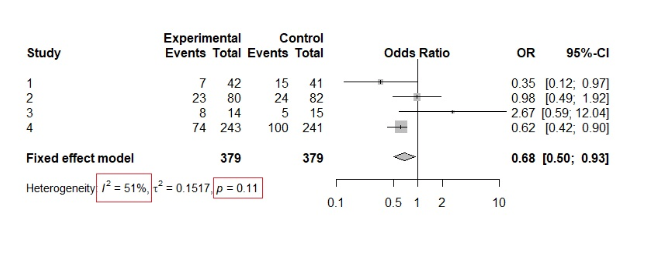
We zien dat de p-waarde van de chi-kwadraattoets 0,11 is, waarmee de nulhypothese wordt bevestigd en dus homogeniteit wordt gesuggereerd. Als we echter naar de interventies kijken, zien we al enige heterogeniteit in de resultaten. Bovendien is de I²-waarde 51%, wat wijst op een matige tot aanzienlijke heterogeniteit.
Dit is een goed voorbeeld van hoe de χ²-test misleidend kan zijn wanneer er slechts enkele studies in de meta-analyse zijn.
Hoe ga je om met heterogeniteit?
Als je eenmaal variabiliteit in je resultaten hebt ontdekt, moet je er iets aan doen. Hier volgen enkele stappen over hoe u dit probleem kunt aanpakken:
- Controleer je gegevens op fouten – Ga terug en kijk of je misschien iets verkeerd hebt ingetypt
- Doe geen meta-analyse als de heterogeniteit te hoog is – Niet elke systematische review heeft een meta-analyse nodig
- Explore heterogeniteit – Dit kan worden gedaan door subgroepanalyse of meta-regressie
- Uitvoeren van een random effects meta-analyse – Bedenk dat deze aanpak bedoeld is voor heterogeniteit die niet verklaard kan worden omdat het aan toeval te wijten is
- Het veranderen van de effectmaten – Stel dat u het Risicoverschil gebruikt en een hoge heterogeniteit heeft, probeer dan eens Risk Ratio of Odds Ratio
(1) Fletcher, J. Wat is heterogeniteit en is het belangrijk? BMJ 2007; 334 :94
(2) Deeks JJ, Higgins JPT, Altman DG (editors). Hoofdstuk 9: Analyseren van gegevens en uitvoeren van meta-analyses. In: Higgins JPT, Green S (editors). Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 . The Cochrane Collaboration, 2011. Beschikbaar via www.cochrane-handbook.org.
(3) https://www.mathsisfun.com/data/chi-square-test.html