Er zijn verschillende soorten grafieken, afhankelijk van het aantal hoekpunten, het aantal ribben, de onderlinge verbondenheid en de algemene structuur. We zullen in dit hoofdstuk slechts enkele belangrijke typen grafieken bespreken.
Nulgrafiek
Een grafiek zonder ribben wordt een Nulgrafiek genoemd.
Voorbeeld

In de bovenstaande grafiek zijn er drie hoekpunten genaamd ‘a’, ‘b’ en ‘c’, maar er zijn geen ribben tussen hen. Het is dus een Null Graph.
Trivial Graph
Een grafiek met slechts één hoekpunt heet een Trivial Graph.
Example
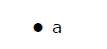
In de hierboven getoonde grafiek is er slechts één hoekpunt ‘a’ met geen andere ribben. Het is dus een triviale grafiek.
Non-Directed Graph
Een non-directed graph bevat wel ribben, maar het zijn geen gerichte ribben.
Voorbeeld
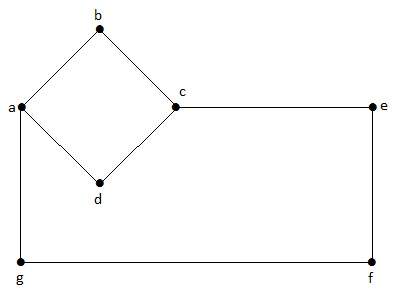
In deze grafiek zijn ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’ de hoekpunten, en ‘ab’, ‘bc’, ‘cd’, ‘da’, ‘ag’, ‘gf’, ‘ef’ de randen van de grafiek. Omdat het een niet-gerichte grafiek is, zijn de ribben ‘ab’ en ‘ba’ hetzelfde. Ook andere randen worden op dezelfde manier beschouwd.
Gerichte grafiek
In een gerichte grafiek heeft elke rand een richting.
Voorbeeld
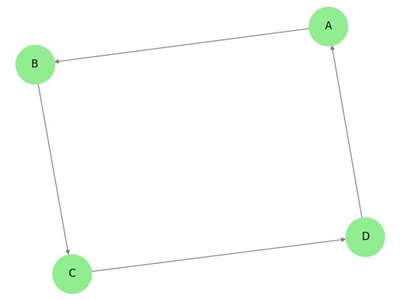
In de bovenstaande grafiek hebben we zeven hoekpunten ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’ en ‘g’, en acht ribben ‘ab’, ‘cb’, ‘dc’, ‘ad’, ‘ec’, ‘fe’, ‘gf’, en ‘ga’. Aangezien het een gerichte grafiek is, is elke rand voorzien van een pijl die de richting aangeeft. Merk op dat in een gerichte grafiek ‘ab’ verschilt van ‘ba’.
Eenvoudige grafiek
Een grafiek zonder lussen en zonder parallelle ribben wordt een eenvoudige grafiek genoemd.
-
Het maximum aantal ribben dat mogelijk is in een enkele grafiek met ‘n’ hoekpunten is nC2 waarbij nC2 = n(n – 1)/2.
-
Het aantal mogelijke eenvoudige grafieken met ‘n’ hoekpunten = 2nc2 = 2n(n-1)/2.
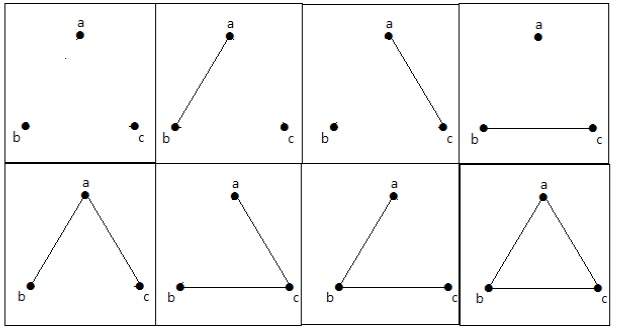
Voorbeeld
In de volgende grafiek zijn er 3 hoekpunten met 3 ribben, wat het maximum is zonder de parallelle ribben en lussen. Dit kan bewezen worden met bovenstaande formules.
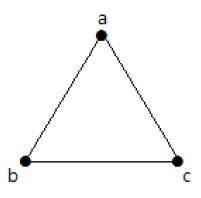
Het maximum aantal ribben met n=3 hoekpunten –
nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
Het maximum aantal eenvoudige grafieken met n=3 hoekpunten –
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
Deze 8 grafieken zijn zoals hieronder weergegeven –
Gesloten grafiek
Een grafiek G wordt verbonden genoemd als er een pad bestaat tussen elk paar hoekpunten. Voor elk hoekpunt in de grafiek moet er ten minste één rand zijn. Zodat we kunnen zeggen dat het verbonden is met een ander hoekpunt aan de andere kant van de rand.
Voorbeeld
In de volgende grafiek heeft elk hoekpunt zijn eigen rand die verbonden is met een andere rand. Het is dus een verbonden grafiek.
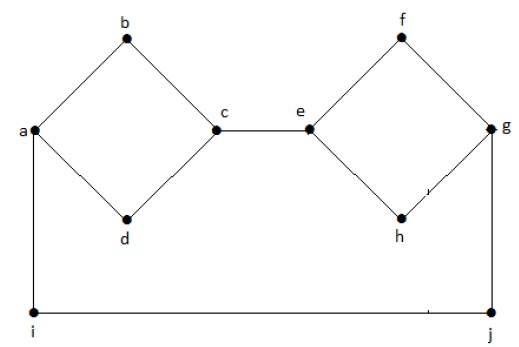
Grafiek zonder verbindingen
Een grafiek G is niet verbonden als hij niet ten minste twee verbonden hoekpunten bevat.
Voorbeeld 1
De volgende grafiek is een voorbeeld van een ontkoppelde grafiek, waarbij er twee componenten zijn, een met ‘a’, ‘b’, ‘c’, ‘d’ hoekpunten en een andere met ‘e’, ‘f’, ‘g’, ‘h’ hoekpunten.
De twee componenten zijn onafhankelijk van elkaar en niet met elkaar verbonden. Daarom wordt dit een ontkoppelde grafiek genoemd.
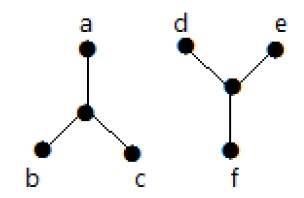
Voorbeeld 2
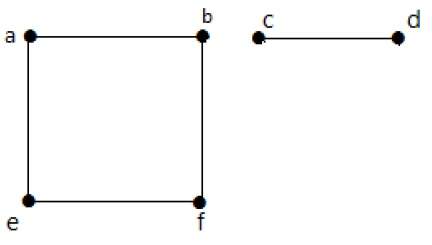
In dit voorbeeld zijn er twee onafhankelijke componenten, a-b-f-e en c-d, die niet met elkaar verbonden zijn. Dit is dus een ontkoppelde grafiek.
Reguliere grafiek
Een grafiek G wordt regelmatig genoemd als alle hoekpunten dezelfde graad hebben. Als in een grafiek de graad van elk hoekpunt ‘k’ is, dan wordt de grafiek een ‘k-reguliere grafiek’ genoemd.
Voorbeeld
In de volgende grafieken hebben alle hoekpunten dezelfde graad. Deze grafieken worden dus regelmatige grafieken genoemd.
In beide grafieken hebben alle hoekpunten graad 2. Ze worden 2-Reguliere Grafieken genoemd.
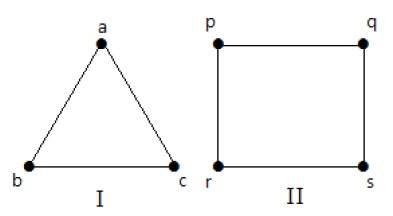
Volledige Grafiek
Een eenvoudige grafiek met ‘n’ onderlinge hoekpunten wordt een volledige grafiek genoemd en wordt aangeduid met ‘Kn’. In de grafiek moet een hoekpunt randen hebben met alle andere hoekpunten, dan heet het een complete grafiek.
Met andere woorden, als een hoekpunt verbonden is met alle andere hoekpunten in een grafiek, dan heet het een complete grafiek.
Voorbeeld
In de volgende grafieken is elk hoekpunt in de grafiek verbonden met alle overige hoekpunten in de grafiek, behalve met zichzelf.
In grafiek I,
| a | b | c | |
|---|---|---|---|
| a | Niet verbonden | Gesloten | Gesloten |
| b | Geconnecteerd | Niet geconnecteerd | Geconnecteerd |
| c | Geconnecteerd | Geconnecteerd | Niet geconnecteerd |
In grafiek II,
| p | q | r | s | |
|---|---|---|---|---|
| p | Niet aangesloten | Gesloten | Gesloten | Connected |
| q | Connected | Not Connected | Connected | Connected |
| r | Connected | Gesloten | Niet aangesloten | Gesloten |
| s | Gesloten | Gesloten | Niet aangesloten | Niet Aangesloten |
Cyclusgrafiek
Een eenvoudige grafiek met ‘n’ hoekpunten (n >= 3) en ‘n’ ribben wordt een cyclusgrafiek genoemd als alle ribben een cyclus van lengte ‘n’ vormen.
Als de graad van elk hoekpunt in de grafiek twee is, dan heet het een cyclusgrafiek.
Notatie – Cn
Voorbeeld
Kijk eens naar de volgende grafieken –
-
Grafiek I heeft 3 hoekpunten met 3 ribben die samen een cyclus ‘ab-bc-ca’ vormen.
-
Grafiek II heeft 4 hoekpunten met 4 ribben die samen een cyclus ‘pq-qs-sr-rp’ vormen.
-
Grafiek III heeft 5 hoekpunten met 5 ribben die samen een cyclus ‘ik-km-ml-lj-ji’ vormen.
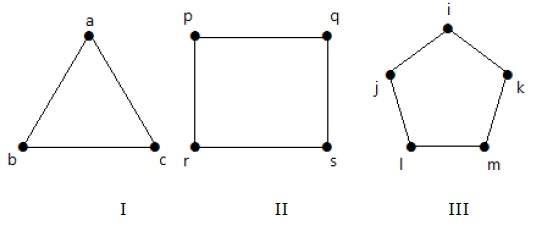
Dus alle gegeven grafieken zijn cyclusgrafieken.
Wielgrafiek
Een wielgrafiek wordt verkregen uit een cyclusgrafiek Cn-1 door een nieuw hoekpunt toe te voegen. Dat nieuwe hoekpunt heet een Hub die verbonden is met alle hoekpunten van Cn.
Notatie – Wn
No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)
Voorbeeld
Kijk eens naar de volgende grafieken. Het zijn allemaal wielgrafieken.
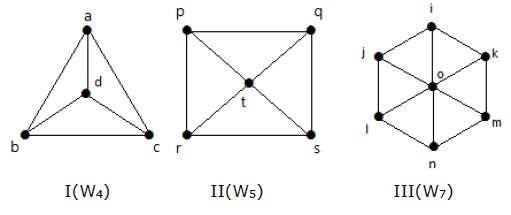
In grafiek I wordt deze verkregen uit C3 door een hoekpunt in het midden toe te voegen met de naam ‘d’. Het wordt aangeduid als W4.
Number of edges in W4 = 2(n-1) = 2(3) = 6
In grafiek II wordt het verkregen uit C4 door in het midden een hoekpunt toe te voegen met de naam ’t’. Het wordt aangeduid als W5.
Number of edges in W5 = 2(n-1) = 2(4) = 8
In grafiek III wordt het verkregen uit C6 door in het midden een hoekpunt toe te voegen met de naam ‘o’. Deze wordt aangeduid als W7.
Number of edges in W4 = 2(n-1) = 2(6) = 12
Cyclische grafiek
Een grafiek met ten minste één cyclus wordt een cyclische grafiek genoemd.
Voorbeeld
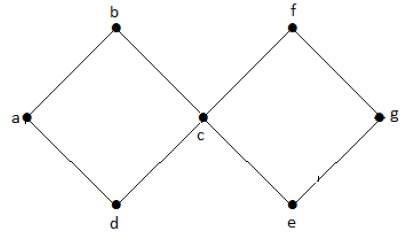
In de bovenstaande voorbeeldgrafiek hebben we twee cycli a-b-c-d-a en c-f-g-e-c. Daarom heet het een cyclische grafiek.
Acyclische grafiek
Een grafiek zonder cycli heet een acyclische grafiek.
Voorbeeld
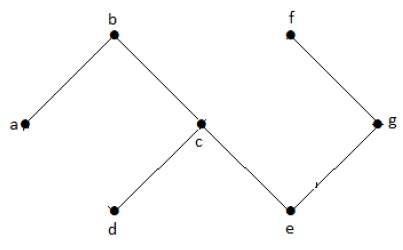
In de bovenstaande voorbeeldgrafiek hebben we geen cycli. Het is dus een niet-cyclische grafiek.
Bipartiete grafiek
Een eenvoudige grafiek G = (V, E) met vertexpartitie V = {V1, V2} wordt een bipartiete grafiek genoemd als elke rand van E een vertex in V1 verbindt met een vertex in V2.
In het algemeen heeft een bipartiete grafiek twee verzamelingen hoekpunten, laten we zeggen, V1 en V2, en als er een rand wordt getekend, moet die een willekeurig hoekpunt in verzameling V1 verbinden met een willekeurig hoekpunt in verzameling V2.
Voorbeeld
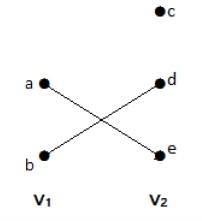
In deze grafiek ziet u twee verzamelingen hoekpunten – V1 en V2. Hier verbinden twee ribben, genaamd ‘ae’ en ‘bd’, de hoekpunten van twee verzamelingen V1 en V2.
Volledige bipartiete grafiek
Een bipartiete grafiek ‘G’, G = (V, E) met partitie V = {V1, V2} wordt een volledige bipartiete grafiek genoemd als elk hoekpunt in V1 verbonden is met elk hoekpunt van V2.
In het algemeen verbindt een volledige bipartiete grafiek elk hoekpunt uit verzameling V1 met elk hoekpunt uit verzameling V2.
Voorbeeld
De volgende grafiek is een volledige bipartiete grafiek omdat zij ribben heeft die elk hoekpunt uit verzameling V1 met elk hoekpunt uit verzameling V2 verbinden.
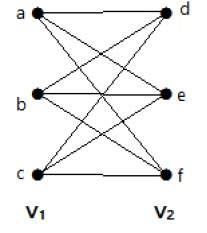
Als |V1| = m en |V2| = n, dan wordt de volledige bipartiete grafiek aangeduid met Km, n.
-
Km,n heeft (m+n) hoekpunten en (mn) ribben.
-
Km,n is een regelmatige grafiek als m=n.
In het algemeen is een volledige tweepartiete grafiek geen volledige grafiek.
Km,n is een volledige grafiek als m=n=1.
Het maximale aantal ribben in een bipartiete grafiek met n hoekpunten is
Als n=10, k5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25
Zo ook K6, 4=24
K7, 3=21
K8, 2=16
K9, 1=9
Als n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20
Zo ook K6, 3=18
K7, 2=14
K8, 1=8
‘G’ is een bipartiete grafiek als ‘G’ geen cycli van oneven lengte heeft. Een speciaal geval van een bipartiete grafiek is een stergrafiek.
Stergrafiek
Een volledige bipartiete grafiek van de vorm K1, n-1 is een stergrafiek met n-vertices. Een stergrafiek is een volledige bipartiete grafiek als een enkel hoekpunt tot de ene groep behoort en alle overige hoekpunten tot de andere groep.
Voorbeeld
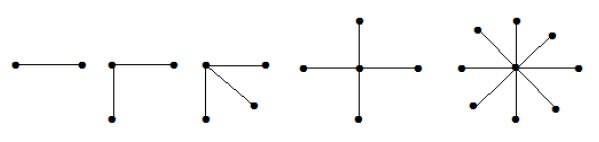
In de bovenstaande grafieken zijn van de ‘n’ hoekpunten alle ‘n-1’ hoekpunten met een enkel hoekpunt verbonden. Het zijn dus stergrafieken in de vorm K1, n-1.
Volledig van een grafiek
Laat ‘G-‘ een eenvoudige grafiek zijn met enkele hoekpunten als die van ‘G’ en een rand {U, V} is aanwezig in ‘G-‘, als de rand niet aanwezig is in G. Dit betekent dat twee hoekpunten in ‘G-‘ aangrenzend zijn als de twee hoekpunten niet aangrenzend zijn in G.
Als de ribben die in grafiek I bestaan, afwezig zijn in een andere grafiek II, en als zowel grafiek I als grafiek II worden gecombineerd om een volledige grafiek te vormen, dan worden grafiek I en grafiek II complementen van elkaar genoemd.
Voorbeeld
In het volgende voorbeeld heeft grafiek-I twee ribben ‘cd’ en ‘bd’. Het complement van grafiek-II heeft vier ribben.
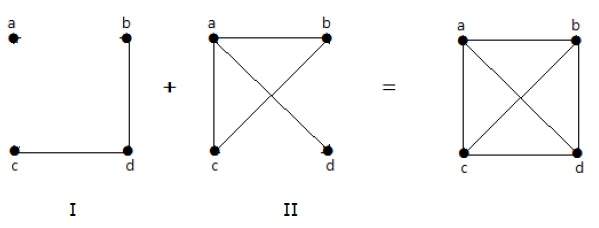
Merk op dat de ribben in grafiek-I niet voorkomen in grafiek-II en vice versa. De combinatie van beide grafieken geeft dus een volledige grafiek van ‘n’ hoekpunten.
Noot – Een combinatie van twee complementaire grafieken geeft een volledige grafiek.
Als ‘G’ een eenvoudige grafiek is, dan
|E(G)| + |E(‘G-‘)| = |E(Kn)|, waarbij n = aantal hoekpunten in de grafiek.
Voorbeeld
Laat ‘G’ een eenvoudige grafiek zijn met negen hoekpunten en twaalf ribben, vind het aantal ribben in ‘G-‘.
U hebt, |E(G)| + |E(‘G-‘)| = |E(Kn)|
12 + |E(‘G-‘)| =