Net als bij cake kun je 2 kleine stukjes hebben of 1 stuk dat twee keer zo groot is en het is toch evenveel. Daarom zijn veel breuken gelijkwaardig, zoals 2/5 en 4/10.


Elk getal kan als breuk worden geschreven
Elk geheel getal boven de 1 kan als breuk worden geschreven, omdat het totaal aantal delen in elk ongedeeld geheel één is.
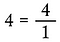
Vermenigvuldig breuken recht over
Vermenigvuldig breuken eenvoudig, gewoon recht over elkaar vermenigvuldigen.
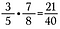
Note: Gemengde getallen moeten eerst worden omgezet in oneigenlijke breuken, lees verder voor meer hierover.
Multiply By Any Form of One Anytime
Het getal 1 wordt de vermenigvuldigingsidentiteit genoemd omdat we het met elk getal kunnen vermenigvuldigen en het getal hetzelfde blijft. Dit is belangrijk voor breuken, omdat we vaak het uiterlijk van een breuk moeten veranderen zonder de waarde ervan te veranderen.
Zo kan ik bijvoorbeeld 1/3 veranderen in de equivalente breuk 3/9 door te vermenigvuldigen met 3/3.
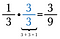
Add and Subtract Equal Sized Parts
Bij het optellen en aftrekken van breuken moeten de noemers gelijk zijn. Dat is logisch. Als we delen willen samenvoegen of weghalen, moeten we het over delen van gelijke grootte hebben, anders zou het verwarrend worden.
Wat doe je dan als je breuken niet dezelfde grootte hebben?
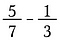
Multiply by a form of one to change the denominators into a common size. In wezen verdelen we de breuken in kleinere stukken tot ze even groot zijn. Dit wordt het vinden van een gemeenschappelijke noemer genoemd.
Eerlijk gezegd is elke gemeenschappelijke noemer goed, maar mensen geven er de voorkeur aan de kleinste te vinden. In dit geval is 21 het kleinste getal waar 7 en 3 in gaan zonder rest. Dus vermenigvuldig de eerste breuk met 3/3 en de tweede met 7/7.
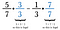
Als je de kleinste gemene deler niet kunt bedenken, kun je altijd elke breuk vermenigvuldigen met de tegenovergestelde noemer. Soms, zoals in dit geval, blijkt dat de kleinste gemene deler te zijn.
Als de noemers overeenkomen, trek je de tellers van elkaar af om 8/21 te krijgen.
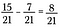
Dit werkt zoals je zou verwachten. Picturaal, begin met 15 stukken van 21 in totaal.

Verwijder de kleuring van 7 van de 15 blauwe blokken.

Waardoor 8/21 overblijft zoals verwacht.
Wissel eerst gemengde getallen uit
Een gemengd getal is de combinatie van een geheel getal en een breuk.
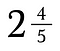
Gemengde getallen gaan niet goed samen met andere breuken. Het is een goed idee om ze eerst om te zetten in oneigenlijke breuken.
Note: een oneigenlijke breuk is een breuk waarvan de teller groter is dan de noemer en dus een waarde groter dan één heeft.
Een gemengd getal omzetten is echt optellen
Om 2 en 4/5 om te zetten in een oneigenlijke breuk tel je 2 + 4/5.
Stap 1: Begin met 2 te herschrijven als 2/1.
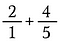
Stap 2: Vermenigvuldig 2/1 met 5/5 om een gelijkwaardige breuk van 10/5 te maken die de gewenste gemene deler van 5 heeft.
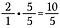
Stap 3: Tel 10/5 + 4/5 bij elkaar op.
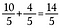
Onze uitkomst is de equivalente oneigenlijke breuk 14/5.
Om terug te converteren naar een gemengd getal voer je de deling uit. Bijvoorbeeld, 5 gaat twee keer in 14 (aangezien 5 x 2 = 10) met 4 stukjes over.
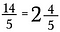
Vergelijk breuken met behulp van het kruisproduct
Stel dat we willen bepalen welke groter is: 5/12 of 6/13.
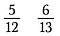
Stap één: Vermenigvuldig een diagonaal en schrijf het product boven de teller.
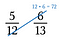
Stap twee: Vermenigvuldig de andere diagonaal en schrijf het product ervan boven de teller.
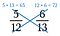
Stap drie: Vergelijk de producten. De kant met het grootste product is de grootste breuk. Dus in dit geval is 5/12 kleiner dan 6/13.
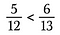
We kunnen ook bepalen of breuken gelijk zijn met behulp van kruisproducten.
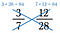
Het kruisproduct van 3/7 en 12/28 is beide 84, dus 3/7 = 12/28.
Alles annuleren wat deelt tot één
Het beste van breuken is dat je veel mogelijkheden kunt vinden om te annuleren. Dat maakt ze snel en gemakkelijk te hanteren.
Stel dat ik de breuk 8/10 heb. Zowel 8 als 10 kunnen herschreven worden met 2 als factor.
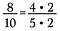
Omdat 2/2 = 1, kan ik de 2’s wegstrepen zodat 4/5 overblijft als de verkleinde breuk.
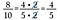
Gebruik deze strategie om ook het vermenigvuldigen van breuken eenvoudiger te maken.
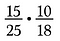
Begin met het herschrijven van elk getal in factoren.
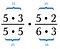
Verwijder alle getallenparen die delen tot 1. Bijvoorbeeld, 5/5 = 1.
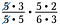
Ik heb nog een paar 5’s en een paar 3’s die ook delen door 1.
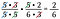
Oeps! Ik had 6 kunnen herschrijven als 2 x 3 en een paar 2’en kunnen schrappen. Het is niet erg als je een factor mist, ga gewoon door tot je ze allemaal hebt.
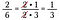
Als ik 15/25 maal 10/18 rechtstreeks had vermenigvuldigd, zou dat een hoop rekenwerk zijn geweest; met behulp van opzeggen verklein ik de breuken en wordt het eenvoudiger om te vermenigvuldigen.
Vermenigvuldiging gebruiken om breuken te delen
Het concept van het delen van breuken is eenvoudig met eenvoudige voorbeelden zoals:

Er zijn twee helften in een geheel, daarom zijn er 10 helften in 5 gehelen.
Maar het concept wordt lastig met meer ingewikkelde breuken.
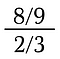
Om dit probleem op te lossen maken we gebruik van twee feiten:
- We kunnen vermenigvuldigen met elke vorm van één (d.w.z.d.w.z. alles over zichzelf)
- Vermenigvuldigen met het reciproke van 3/2, dat is 2/3, levert 1 op door te annuleren
Stap één: Begin met vermenigvuldigen met de reciproke over zichzelf.
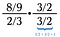
Nu hebben we twee kleinere problemen op te lossen (blauw en groen).
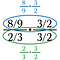
Step twee: Annuleer alles wat deelt tot 1 in de onderste (groene) breuk. Dit moet altijd 1 opleveren.

Nu houden we het bovenste probleem over om op te lossen.
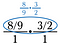
Step drie: Gebruik opzeggen om de breuk vooraf te verkleinen. Nadat u deze verminderingen hebt gemaakt, vermenigvuldigt u ze met elkaar om 4/3 te verkrijgen.

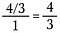
Shortcut
Dit is de lange hand-mechanica van “omdraaien en vermenigvuldigen.”
We kunnen het vermenigvuldigen met de reciproke onderaan overslaan, omdat die altijd opheft tot 1. Daarom hoef je alleen maar de teller te vermenigvuldigen met de reciproke van de noemer.

Bonus: Theorie, voor het geval je geïnteresseerd bent…
Grote vraag! Maak, om te veralgemenen, twee breuken met de letters a, b, c en d om vier verschillende getallen weer te geven.
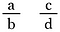
Vermenigvuldig beide breuken met b-d (zo kunnen we de noemers opheffen).
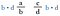
Nu heffen we de b’s links en de d’s rechts op, omdat ze delen tot 1. We hebben geen breuken meer, alleen de producten d-a en c-b.
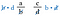
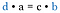
Kijk terug naar de oorspronkelijke breuken. Dit zijn dezelfde producten als wanneer we de diagonalen hadden vermenigvuldigd. Daarom is de kortere weg de vergelijking van het kruisproduct.
❤ STAY CONNECTED ❤
Blijf op de hoogte van alles waar Math Hacks mee bezig is!