Inleiding
Deze pagina behandelt de continuïteitsvergelijking, die massabehoud afdwingt in een Euleriaanse analyse. Dit is strikt genomen geen beschrijving van materiaalgedrag, maar de resulterende vergelijking wordt vaak gebruikt als een identiteit om constitutieve modellen die materiaalgedrag beschrijven, algebraïsch te manipuleren. Het is dus de moeite van het bestuderen waard. Zij staat ook centraal in de analyse van vloeistofstromingen, omdat klassieke vloeistofanalyses niet Lagrangiaans kunnen zijn, omdat de posities van alle vloeistofdeeltjes op t = 0 onbekend zijn.
Behoud van massa
De continuïteitsvergelijking weerspiegelt het feit dat massa behouden blijft in elke niet-nucleaire continuummechanische analyse. De vergelijking wordt opgesteld door de snelheid waarmee de massa in en uit een controlevolume stroomt bij elkaar op te tellen, en de netto-instroom gelijk te stellen aan de snelheid van de verandering van de massa daarin. Dit wordt geïllustreerd in de onderstaande figuur.
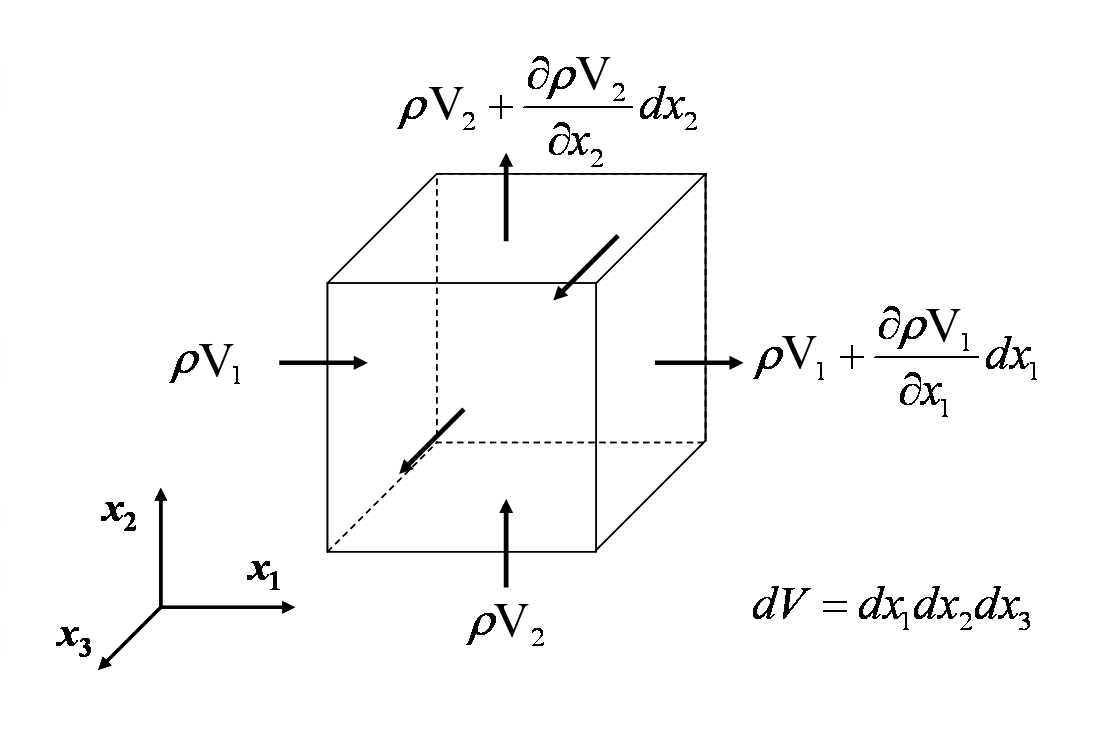
Uitrekening van alle massastromen in en uit het differentiële regelvolume geeft
Cancellering van de termen en deling door \(dx_1 dx_2 dx_3) geeft
en herschikken geeft
Dit kan beknopt geschreven worden als

Belangrijke punten
Dit zijn de laatste, volledige, en meest algemene vormen van de continuïteitsvergelijking die het behoud van massa afdwingt. Ze geldt voor alle materialen, niet alleen voor vloeistoffen. Dus ook voor vaste stoffen. Merk op dat het een enkele scalaire vergelijking is en Euleriaans van aard is omdat de gradiënttermen ({partieel x_i}) zijn, en niet ({partieel x_i}). Men kan zich afvragen of er een Lagrangiaanse tegenhanger is van de Euleriaanse vorm hiervan. Die is er. Deze wordt meestal geschreven als
Dit stelt eenvoudig dat de differentiële massakomp in de vervormde toestand gelijk moet zijn aan zijn oorspronkelijke waarde(\rho_o dV_o\) in de onvervormde toestand.
Er zijn verschillende speciale gevallen van de continuïteitsvergelijking.De eerste doet zich voor als de stroming in een stationaire toestand is. In dit geval is de afgeleide ten opzichte van de tijd nul, zodat.
Het tweede speciale geval is dat van incompressibiliteit, d.w.z, \In dit geval is de afgeleide ten opzichte van de tijd nul en kan de afgeleide uit de vergelijking worden weggelaten, zodat er slechts
overblijft.
Merk op dat dit niets anders is dan \(\bf D}) = 0) voor het geval van onsamendrukbare materialen.

Materiaalafgeleide
Het volgende is de moeite van het vermelden waard omdat hiermee de dichtheid en de snelheidsvector gescheiden kunnen worden. De eerste stap is om de productregel toe te passen op de divergentieterm in de continuïteitsvergelijking.
En merk dan op dat({D \rho \over \partial t} + {\bf v} \cdot \nabla \rho) gewoon de materiële afgeleide van de dichtheid is.
\Als het materiaal onsamendrukbaar is, dan kan \(\rho) niet veranderen, dus moet \( {D \rho \over D t} \) nul zijn, en dan delen door (\rho) (omdat het niet nul is) om te krijgen

Continuïteitsvergelijking Voorbeeld
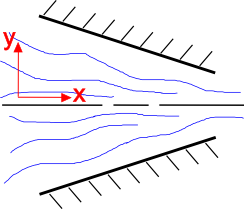
Het is intuïtief dat de vloeistofstroming sneller wordt naarmate de doorsnede kleiner wordt, zoals hiernaast te zien is. De continuïteitsvergelijking verklaart dit. Beschouw een 2-D, stationair stromingsveld van een onsamendrukbare vloeistof. De continuïteitsvergelijking voor deze situatie is
Begin met het bekijken van de y-component van de stroming, \(v_2\). De geometrie van de convergerende straalpijp dwingt de (v_2) component omhoog te stromen als \(y \lt 0) en omlaag te stromen als \(y \gt 0). Dus \(v_2 \gt 0) als \(y \lt 0) en \(v_2 \lt 0) als \(y \gt 0).
En dat betekent dat de vloeistofstroom versnelt.