Concaaf vs. convex?

Wat is het verschil tussen concaaf en convex?

Als we het verschil tussen concaaf en convex op de meest algemene manier zouden beschrijven, zouden we zeggen dat elk hol, komvormig voorwerp concaaf is, terwijl elk voorwerp dat lijkt op een rugbybal of voetbal een convexe vorm heeft. Maar misschien is de reden waarom convex en concaaf zo vaak verkeerd worden gebruikt, dat de twee woorden niet zo eenvoudig zijn als we zouden willen.

De meeste grammaticabronnen benadrukken hoe het gebruik van mnemonics mogelijk is voor het ontcijferen van convex en concaaf door de woordgrot. Terwijl de notie van het associëren van concave met de gebeurtenis van iets “caving-in” helpt leren over oppervlakte-eigenschappen, is het verwarrend om dit idee te relateren aan onderwerpen waarbij grafieken betrokken zijn.

Om te begrijpen hoe concave en convex van elkaar verschillen, moeten we leren hoe elke term wordt gebruikt in de hoedanigheid van wiskunde, spiegels, lenzen, en, ten slotte, binnen creatief schrijven. Als je eenmaal hebt besloten in welke context je woorden als concaaf en convex wilt gebruiken, zal het leren van hun technische aspecten je meer vertrouwen geven over het gebruik ervan in het dagelijks spraakgebruik.

Wat betekent concaaf?

Concaaf wordt gebruikt als een bijvoeglijk naamwoord of zelfstandig naamwoord om de vorm van een voorwerp of oppervlak te beschrijven dat naar binnen is gebogen of hol is, zoals een kom. Voorbeelden van concave in een zin zijn,

“Ze schepte het ijs uit de kom, een holle voetafdruk achterlatend.”

Volgens The Oxford Dictionary of Word Histories stamt het woord concave uit het laat-Middeleeuws Engels. Concave en concavity vormen de Latijnse term concavus (con- en cavus), wat vertaalt naar ‘samen’ en ‘hol’ (“Concave,” 110).

Synoniemen van concaaf zijn onder meer:

Gedeukt, ingedrukt, afgeplat, hol, ingesprongen, verzonken en verzonken.

Antoniemen van concaaf zijn onder andere:

bollend, gewelfd, uitpuilend, uitpuilend, uitpuilend.

Wat betekent convex?

Het woord convex, of convexiteit, is een bijvoeglijk naamwoord dat een voorwerp of oppervlak beschrijft dat rond of gebogen is. Met betrekking tot voorwerpen, het midden oppervlak van een convexe object is breder dan de buitenste hoek. Voorbeelden van convexiteit in een zin zijn,

“Ik ben in de gifsumak gevallen en heb nu rode, convexe bulten over mijn hele huid.”

Synoniemen van convex zijn onder andere:

gebogen, gebogen, uitpuilend, verheven.

Antoniemen van convex zijn onder andere:

Depressed, sinking.

Concave vs convexe functies

Een convexe functie stelt een ononderbroken lijn op een grafiek voor waar het middelpunt, of mediaan geheel getal van een domein, niet hoger is dan het gemiddelde van het interval. Een concave functie is precies het tegenovergestelde van een convexe functie, omdat f(x) alleen concaaf is als f(x) negatief is. Om de verschillen duidelijker te maken, volgt hier een korte opsomming van hoe de termen zich tot elkaar verhouden:

Concaaf naar boven = convex = convex naar beneden

Concaaf naar beneden = concaaf = convex naar boven

Het verschil tussen concave en convexe functies komt duidelijker naar voren als we naar een grafiek kijken. Merk op hoe de convexe functie zich naar boven opent, terwijl de concave functie zich naar beneden opent.

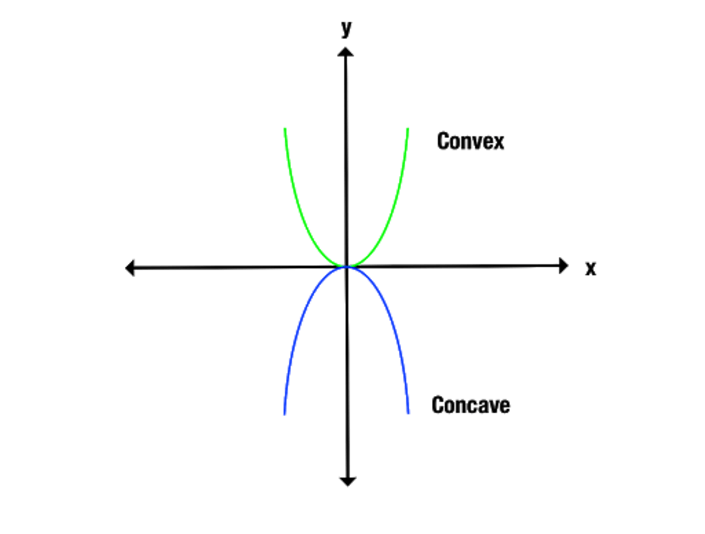
Een andere manier om concave en convexe functies te onderscheiden is door punten op de grafiek langs de x-as met elkaar te verbinden. Een concave functie verbindt alleen lijnen onder de grafiek, terwijl een convexe functie alleen lijnen boven de grafiek oplevert.

We kunnen bovendien calculus gebruiken om te bepalen of een functie al dan niet convex of concaaf is. Als de tweede afgeleide van f(x) groter is dan nul, dan is de functie convex. Maar als de tweede afgeleide van f(x) kleiner is dan nul, dan is de functie concaaf.

Convexe vs. holle veelhoeken

Geen paniek, maar de woorden convex en concaaf worden ook voor meetkunde gebruikt. Over convexe en concave vormen wordt het vaakst gesproken in verband met veelhoeken, dat zijn vormen met minimaal drie zijden en hoeken.

Reguliere veelhoeken bestaan met gelijke zijden en hoeken, maar convexe en concave veelhoeken zijn iets gecompliceerder. Convexe veelhoeken bevatten binnenhoeken die kleiner zijn dan 180 graden, terwijl concave veelhoeken een of meer binnenhoeken bevatten die groter zijn dan 180 graden.

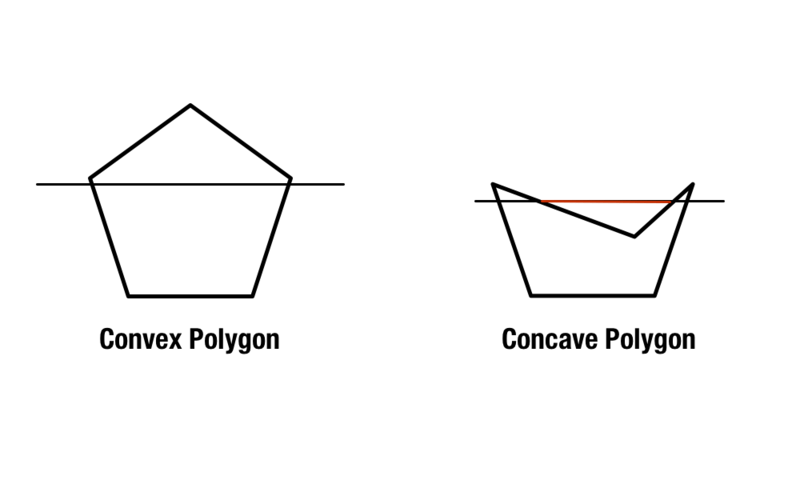
Een tweede methode om concave en convexe veelhoeken te identificeren is door twee diagonale lijnen over de vorm te trekken, beginnend bij de hoeken van de vorm. Als elke lijn binnen de vorm bestaat, is de vorm convex. Als er ten minste één lijn buiten de vorm loopt, is hij concaaf.

Concave vs. convexe spiegels

De woorden concaaf en convex worden vaak gebruikt bij de bespreking van optische voorwerpen, zoals spiegels en lenzen. Elk convex oppervlak zal naar buiten uitsteken, net als een luchtbel, wat het effect van breedheid geeft. Convexe spiegels worden vaak aangetroffen in parkeergarages, waar bestuurders een breed zicht rond hoeken of potentiële dode hoeken nodig hebben.

Een concave spiegel daarentegen is naar binnen gebogen en geeft een uitvergrote reflectie die op zijn kop staat. Zoals de School of Physics van de University of South Wales heeft aangetoond, kan iedereen met een glimmende lepel deze waarneming testen door naar zijn spiegelbeeld in de lepel te kijken. Op het holle oppervlak van de lepel, waar je je eten oppakt, wordt je weerkaatsing eng vervormd, en lijk je ondersteboven te staan. Maar als je de lepel omdraait naar de bolle kant, zal je spiegelbeeld rechtop staan en kleiner zijn.

Reflecties verschillen zo sterk tussen convexe en concave oppervlakken omdat, of het oppervlak nu naar buiten of naar binnen buigt, de spiegel zelf deel uitmaakt van een bol. Omdat het oppervlak van een bol niet vlak is, zal het licht dat door het oppervlak wordt weerkaatst verschillende afstanden afleggen voordat het de spiegel raakt.

Afhankelijk van met welk deel van het oppervlak het licht in aanraking komt, kan een lichtstraal weerkaatsen op nabijgelegen oppervlakken, zodat een meer geconcentreerd zichtbaar gebied ontstaat. Dit is de reden waarom, als men naar de binnenkant van een lepel kijkt, men misschien alleen de weerkaatsing ziet van wat het dichtst bij het oppervlak van de lepel is – ook al lijkt het nog kleiner. Bovendien, als u uw vinger in de lepel zou plaatsen, kan het oppervlak van de spiegel twee of drie verschillende weerkaatsingen op hetzelfde moment produceren.

Concave lens vs. convexe lens

Concave en convexe lenzen komen voor in alledaagse voorwerpen zoals brillen, contactlenzen, verrekijkers en telescopen. Net als de wetenschap achter de weerkaatsing van licht op convexe en concave spiegels, bestaan er ook patronen voor de manier waarop licht door concave en convexe lenzen valt om een zichtbaar beeld te produceren.

Convexe lenzen

Volgens Manocha Academy worden convexe lenzen convergerende lenzen genoemd vanwege hun vermogen om beelden te produceren die worden verkleind, vergroot, of naar binnen gekeerd. Hoe nauwkeurig een beeld door de bolle lens verschijnt, hangt af van hoe dicht het voorwerp zich bij het brandpunt van de lens bevindt. Voor elke bolle lens zijn er symmetrische brandpunten aan weerszijden van de lens.

Hoe nauwkeurig een voorwerp door een bolle lens wordt weergegeven, wordt voorspeld met drie principes:

Principe 1: Elke lichtstraal die door een bolle lens gaat, is evenwijdig aan de hoofdas, die een centrale lijn is die door het absolute middelpunt van een bolvormige lens gaat. Zodra het licht de lens raakt, breekt het licht en gaat het door het brandpunt aan de andere kant. Passerende lichtstralen die evenwijdig zijn aan de hoofdas reizen boven het voorwerp voor de lens.

Principe 2: Elke lichtstraal die door het middelpunt van een bolle lens gaat, zal aan de andere kant in een rechte lijn verder gaan.
Beginsel 3: Elke lichtstraal die door een brandpunt aan dezelfde kant als het voorwerp valt, zal bij contact met de lens breken en aan de andere kant evenwijdig worden aan de hoofdas.

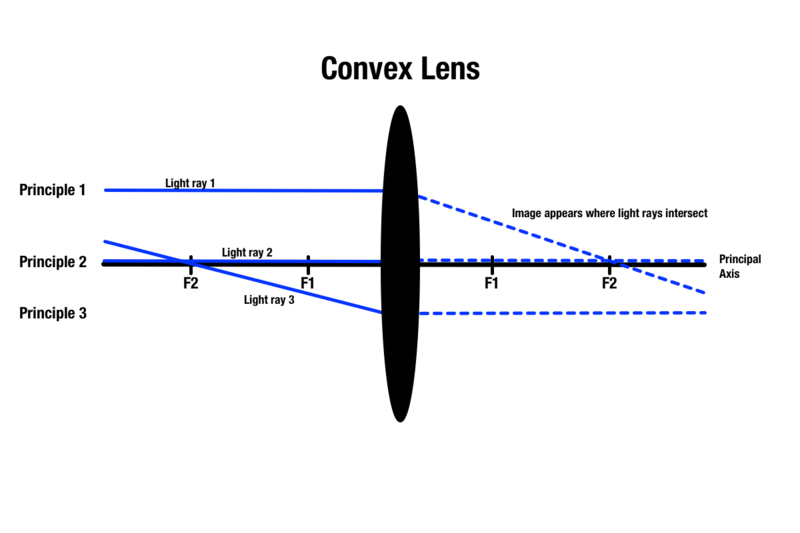
Hoewel er drie beginselen zijn voor het voorspellen van de beeldkwaliteit door een bolle lens, kunnen slechts twee beginselen op een voorwerp worden toegepast bij het tekenen van een straaldiagram. Elke twee principes zullen een snijpunt van licht aan de andere kant van de lens opleveren, dat het gebied aangeeft waar het beeld van het voorwerp verschijnt.

Hoe verder een voorwerp zich van een bolle lens bevindt, hoe kleiner het beeld aan de andere zijde zal zijn, en hoe dichter een voorwerp zich bij de bolle lens bevindt, hoe groter het zal lijken. Een voorwerp dat zich voorbij het dichtstbijzijnde brandpunt bevindt, geeft een groter beeld achter het voorwerp. Zoals Manocha Academy opmerkt, wordt dit type lensvergroting gebruikt voor optische instrumenten zoals vergrootglazen.

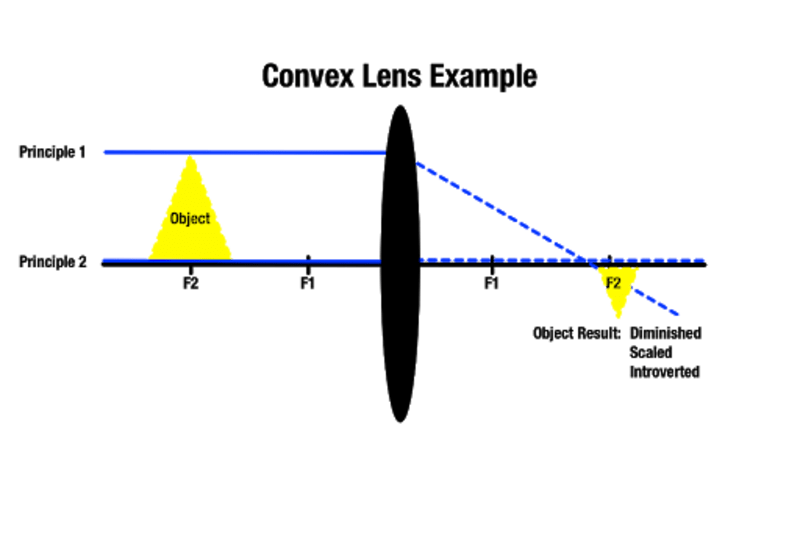
Afhankelijk van het brandpunt waar een voorwerp zich bevindt, is het mogelijk een beeld te produceren dat bij benadering groter is. Het is ook mogelijk om echte beelden te maken die niet zichtbaar zijn als de passerende lichtstralen elkaar nooit snijden omdat ze aan de andere kant evenwijdig zijn. In dit geval bestaat het geproduceerde beeld op een oneindige afstand.

Concave lenzen

Een concave lens zal een dikkere diameter hebben, en een dunner centrum omdat een concave lens naar binnen is gebogen. De vorm van holle lenzen zorgt ervoor dat het licht zich verspreidt zodra het contact maakt met de lens, waardoor virtuele voorwerpen kleiner lijken. Het vermogen van de concave lens om licht te verspreiden maakt het een ideale lens voor hulpmiddelen zoals zaklampen, waar een centrale lichtbron over een groter oppervlak kan worden gebruikt.

Concave lenzen produceren beelden met drie principes die vergelijkbaar zijn met convexe lenzen:

Principe 1: Elke lichtstraal die zich boven het object en evenwijdig aan de hoofdas beweegt, zal bij contact met de lens breken en verschijnen alsof hij afkomstig is uit de richting van het dichtstbijzijnde brandpunt.

Beginsel 2: Elke lichtstraal die door het midden van de holle lens gaat, gaat erdoor zonder breking.
Beginsel 3: Elke lichtstraal die naar een brandpunt aan de andere kant van de holle lens wordt gericht, zal breken en evenwijdig worden aan de hoofdas.

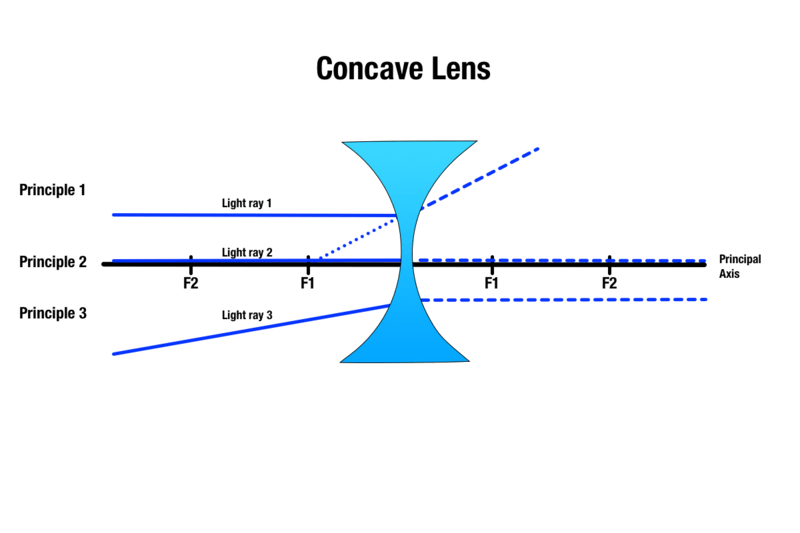
Hoewel de grootte van het beeld van het voorwerp varieert afhankelijk van de afstand van het voorwerp tot een holle lens, is het geproduceerde beeld altijd virtueel, rechtopstaand en kleiner, en verschijnt het aan dezelfde kant van de lens als het voorwerp.

Concaaf vs. convex in schrift

De woorden concaaf en convex zijn tegengesteld aan elkaar, en ze beschrijven in wezen de vorm van voorwerpen of oppervlakken op dezelfde manier waarop we woorden contrasteren als:

• klein vs. groot
• Tall vs. short
• Slim vs. wide
• Round vs. flat

Omdat concave en convexe technische woorden zijn, kan het gebruik ervan beschrijvend voor proza een meer metaforische of abstracte interpretatie opleveren voor een gewoon publiek. Wat dit betekent is dat als schrijvers besluiten om concaaf of convex te gebruiken buiten het gebied van hun typische gebruik, de schrijver moet beslissen hoe duidelijk ze willen dat hun schrijven is.

Kijk naar het bijvoeglijk naamwoord

Een prominent voorbeeld van het gebruik van concaaf of convex in de literatuur zijn de geschriften van de Amerikaanse auteur David Foster Wallace (of kortweg DFW). DFW is berucht om zijn complexe en technische schrijfstijl – en ja, hij gebruikte convex en concaaf om zelfstandige naamwoorden meerdere malen te beschrijven. Wallace gebruikt concaaf en convex in de volgende voorbeelden:

“Mijn handoog was in orde, maar ik was noch groot noch snel, had een bijna holle borst en polsen die zo dun waren dat ik ze met duim en pink kon buigen…”

– “Tennis, Trigonometrie, Tornados: A Midwestern Boyhood,” Harper’s Magazine.

“…poppenogen die opengaan met de trekkracht van een hartkoord, hol waar ik bol ben.”

– “Order and Flux in Northampton,” Conjunctions.

Het punt van het gebruik van DFW-voorbeelden is niet alleen om te laten zien hoe schrijvers convex of concaaf hebben gebruikt buiten de wiskundige context, maar eerder om schrijvers te laten overwegen of het gebruik van technische of abstracte termen nuttig is om duidelijk te communiceren met hun publiek.
In het eerste voorbeeld van DFW is het gebruik van concaaf zinvol omdat hij de structuur van iets beschrijft. Maar het gebruik van concaaf en convex om niet-objectieve zelfstandige naamwoorden te beschrijven, zoals gevoelens of gedachten, heeft de neiging de betekenis te vertroebelen van wat we proberen uit te leggen. Het tweede DFW voorbeeld bewandelt een dunne lijn bij het gebruik van convex en concaaf, omdat hun gebruik zowel letterlijk als metaforisch is.

FAQ: Verwante termen

Wat is een functie?

Een functie is de vergelijking van een lijn op een grafiek. Functies zijn verschillend voor elke lijn op een grafiek, maar ze hebben de algemene vorm,

f(x) = x + 1

Bij elke lijnfunctie is de afhankelijke variabele meestal f(x), terwijl elke onbekende variabele binnen de functie een onafhankelijke variabele wordt genoemd.

Wat is het domein?

Het domein is een verzameling onafhankelijke variabelen op een grafiek die overeenkomt met de functie van een lijn. Domeinen zijn belangrijk om te begrijpen, omdat zij specifieke punten op de grafiek lokaliseren die overeenkomen met elke reële uitvoer van een vergelijking.

Wat is het bereik?

Het bereik van een functie vertegenwoordigt elke mogelijke waarde langs de x- of y-as op een grafiek die een geldige waarde voor de afhankelijke variabele oplevert. Alle minimale en maximale gehele getallen worden geïdentificeerd door variabelen voor de x- of y-as te substitueren.

Wat is een interval?

Een interval is een verzameling getallen die de gehele getallen van een lijn voorstellen, ook wel het domein genoemd. Een gesloten interval omvat twee eindige punten van een lijn, waarbij de lijn niet meer bestaat buiten het bereik van een geheel getal. Een open interval is een verzameling gehele getallen die niet het absolute einde van het domein van een lijn vertegenwoordigen.

Test jezelf!

Zie hoe goed je het verschil tussen convex en concaaf begrijpt met de volgende meerkeuzevragen:

1. Terwijl je naar een glimmende lepel kijkt, merk je dat je spiegelbeeld ondersteboven is. Het oppervlak van de lepel is een _________ oppervlak.
   a. Convex
   b. Spiegel
   c. Concaaf
   d. Metaal
2. In termen van grafische functies, wordt een convexe functie soms genoemd:
   a. Concaaf naar boven
   b. Convex naar beneden
   c. Concaaf naar beneden
   d. A en B
3. Welke van de volgende beschrijft niet een concaaf oppervlak:
   a. Holle halve bol
   b. Ooglens
   c. Graankom
   d. Hemisfeer
4. Welke van de volgende beschrijft niet een convex oppervlak:
   a. Het personage Stewie uit Family Guy
   b. Bol
   c. Parkeergaragespiegel
   d. Voetbal
5. Welke van de volgende vormen kan niet bestaan als een concave veelhoek:
   a. Vijfhoek
   b. Zeshoek
   c. Driehoek
   d. Achthoek

Antwoorden

1. C: Concave
2. D: A en B
3. D: Hemisphere
4. B: Sphere
5. C: Triangle

Bronnen:

1. Bourne, M. “Domain and Range of a Function.” Interactive Mathematics, Jan. 4, 2019.
2. “Concave.” Merriam-Webster Woordenboek, 2019.
3. “Concave.” The Oxford Dictionary of Word Histories, Ed. Chantrell, 2002, p. 110.
4. “Concave and Convex Mirrors.” Manocha Academie, YouTube, 2019.
5. “Concave Lens: Definition & Uses.” Study.com, 2019.
6. “Convex.” Merriam-Webster Dictionary, 2019.
7. “Convexe en Concave Lenzen.” Manocha Academie, YouTube, 2019.
8. “Wiskunde / Inzicht in veelhoeken.” Learnhive Inc., 2018.
9. “Reflectie van een holle spiegel.” UNSW Physics, YouTube, 2017.
10. Wallace, D.F. “Tennis, Trigonometrie, Tornado’s: A Midwestern Boyhood.” Harper’s Magazine, 1991.
11. Wallace, D.F. “Order and Flux in Northampton.” Conjunctions, 1991.
12. Weisstein, Eric W. “Concave Function.” MathWorld-A Wolfram Web Resource, n.d.
13. Weisstein, Eric W. “Convexe Functie.” MathWorld-A Wolfram Web Resource, n.d.

De Word Counter is een dynamische online tool gebruikt voor het tellen van woorden, tekens, zinnen, alinea’s en pagina’s in real time, samen met spelling en grammatica controle.