 |
 |
| HYDROFOILS | ||
| VRAGEN OF OPMERKINGEN | ||
|
|
AUTOR: | Tina Rosado |
| E-MAIL: | [email protected] | |
| COURSE: | 2 | |
| KLAS/JAAR: | 2 | |
BELANGRIJKSTE FUNCTIE-EIS: De romp van de boot buiten het water tillen.
ONTWERP PARAMETER: Draagvleugelboot (het is een folie of vleugel onder water die wordt gebruikt om de romp van de boot op te tillen tot hij helemaal buiten het water is.
GEOMETRIE/STRUCTUUR:
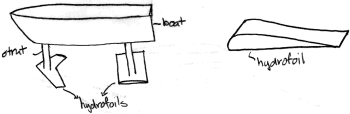
Detail van Hydrofoil Geometrie
UitLEG VAN HOE HET WERKT/ WORDT GEBRUIKT:
1. Bij lage snelheden ligt de romp (de romp van het schip) in het water en zijn de draagvleugels volledig ondergedompeld in het water.
2. Naarmate de snelheid van de boot toeneemt, creëren de draagvleugels lift.
3. Bij een bepaalde snelheid is de door de draagvleugels geproduceerde lift gelijk aan de som van het gewicht van de boot en de lading. Daardoor komt de romp uit het water.
4. In plaats van een toename van de weerstand bij toenemende snelheid, omdat de romp uit het water wordt getild (in tegenstelling tot wat gebeurt in traditionele boten als gevolg van drukweerstand), zorgen de draagvleugels voor een efficiëntere manier van varen. Vermindering van de weerstand draagt bij tot een betere benutting van het voor de voortbeweging van de boot benodigde vermogen.
DOMINANTE FYSICA:
Hoe wordt de lift geproduceerd – Fluid Dynamics.
Voor het doel van dit project zullen twee verklaringen op een algemene en basale manier worden gepresenteerd. Deze theorieën zijn de toepassing van Bernoullis Vergelijking enEulers Vergelijking voor Stroomlijnkrommingseffect.
Bernoullis Vergelijking: Po = P1 + ½
rv1² + rgy1 = P2 + ½rv2² + rgy2
| Variabelen | Eenheden |
| Po Stagnatiedruk | of |
| P Druk | of |
| r Dichtheid | of |
| V Snelheid | of |
| g Gravitatieconstante | of |
| y Hoogte | of |
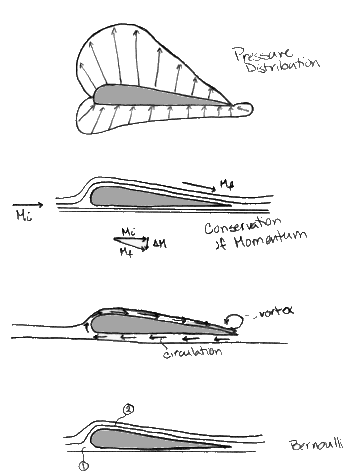
Detail van draagvleugelboot: a) Drukprofiel b) Impulsoverdracht c) Circulatie d) Stroomlijnen
Deze vergelijking is van toepassing op stromingen langs een stroomlijn die kunnen worden gemodelleerd als: inviscide, onsamendrukbaar, stationair, irrotatie en waarvoor de lichaamskrachten conservatief zijn. Ook het verschil in hoogte van de folie (de afstand van de onderste sectie tot de bovenste) is klein genoeg zodat het verschil rgy2 – rgy1 verwaarloosbaar is vergeleken met het verschil van de rest van de termen. Wat overblijft is dat de druk plus de helft van de dichtheid maal de snelheid in het kwadraat gelijk is aan een constante (de stagnatiedruk).
Als de snelheid langs deze stroomlijnen toeneemt, daalt de druk (dit wordt zo belangrijk). De vloeistof die over het bovenste oppervlak van de folie beweegt, beweegt sneller dan de vloeistof op de bodem. Om het impulsmoment te behouden dat veroorzaakt wordt door de rotatie van de wervelingen tegen de wijzers van de klok in, moet er een gelijke maar tegengestelde uitwisseling van impulsmoment zijn met de werveling aan de achterrand van de folie. Dit leidt tot circulatie van de vloeistof rond de folie. De vectortelling van de snelheden resulteert in een hogere snelheid aan het bovenoppervlak en een lagere snelheid aan het onderoppervlak. Wanneer dit op Bernoullis wordt toegepast, wordt waargenomen dat, wanneer de folie door de vloeistof snijdt, de snelheidsverandering de drukval veroorzaakt die nodig is voor de lift. Zoals het diagram laat zien, is de resulterende of netto kracht (kracht= (druk)(oppervlakte)) opwaarts. Deze uitleg kan worden verrijkt met het principe van behoud van momentum.(Momentum = (massa)(snelheid)) Als de snelheid van een deeltje met een initieel momentum wordt verhoogd, dan is er een reactief momentum dat gelijk is in grootte en tegengesteld in richting aan het verschil van de momentums. (Zie diagram).(Mi = Mf + DM)
Eulers Vergelijking: d(p+rgy)/dn = rv²/R
| Variabelen | Eenheden |
| P Druk | of |
| r Dichtheid | of |
| V Snelheid | of |
| g Gravitatieconstante | of |
| y Hoogte | of |
| n Vector in radiale richting | — |
| R kromtestraal van de stroomlijn | of |
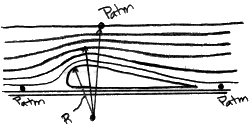
detail van druk op punten boven een vleugelprofiel
Ook hier, wordt de term die naar de hoogte verwijst, verwaarloosbaar geacht in vergelijking met de andere termen in de vergelijking. Deze vergelijking zegt dat naarmate je verder van het middelpunt van de kromtestraal van een stroomlijn gaat, de druk op de stroomlijnen toeneemt. Het bovenste oppervlak van de folie ligt dichter bij het kromtepunt van de stroomlijnen, daarom zal er een lagere druk zijn dan de omgevingsdruk boven de folie. Het verschil tussen de druk aan het bovenoppervlak en de omgevingsdruk aan het onderoppervlak zal een nettodruk opleveren die de lift zal veroorzaken. (Seediagram.)
Aanvalshoek:

Angle of Attack
Zoals het is voorgesteld, wordt de lift veroorzaakt door de dynamica van de vloeistof in de gebieden rond de folie. Maar de lift kan worden geoptimaliseerd door de hydrofoil onder een hoek te plaatsen (ten opzichte van de inkomende vloeistofstroom) die de invalshoek wordt genoemd (zie diagram). Het doel is om de lift-weerstandverhouding te optimaliseren. Deze verhouding hangt af van de vorm van de folie, die in dit geval als een dunne folie wordt beschouwd. Bij een kleine invalshoek neemt de lift snel toe, terwijl de weerstand slechts in geringe mate toeneemt. Na een invalshoek van ~10° neemt de lift langzaam toe tot ~15°, waar hij een maximum bereikt. Na ~15° kan een overtrek optreden. Wanneer de invalshoek 3° tot 4° is, is de verhouding lift:weerstand maximaal.De folie is dus efficiënter bij die hoeken (3°en 4°) met lift-weerstand verhoudingen van ~ 20 tot 25:1
LIMITATIEVE FYSIEKEN:
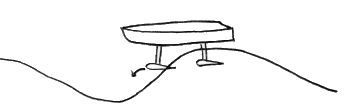
Detail van Hydrofoil Geometrie
Op het eerste gezicht kunnen mensen denken dat afslaan waarschijnlijk een probleem zal zijn bij hydrofoils, net zoals bij luchtschoepen, maar verrassend genoeg is dat niet zo. Een steile invalshoek is niet nodig bij het ontwerp van een draagvleugelboot. Integendeel, kleine invalshoeken worden gebruikt bij draagvleugels om de lift-weerstandverhouding te optimaliseren, zoals eerder uitgelegd.
Wat van primair belang is, is het ontwerp van de folie, de stutten/steunen, en hun positionering. Al deze kenmerken moeten in aanmerking worden genomen. Zo worden de eigenschappen ontworpen om een minimumsnelheid te produceren die de boot van bepaald gewicht zal opheffen en het in folie zal houden.
Een probleem dat een draagvleugelboot kan ondervinden is dat de hoogte van de golven groter is dan de stutten. Ook, als het vaartuig sneller dan de golven reist, de foilscould breken aan de oppervlakte en buiten het water, wat resulteert in een verlies van lift en een negatieve invalshoek wanneer de folie duikt in de volgende golf, waardoor het vaartuig crashen in de zee. Ingenieurs hebben draagvleugels ontworpen om de beperkingen te minimaliseren en de prestaties van de schepen te verbeteren.
PLOTS/GRAPHS/TABLES:
Niet Ingediend
SOMKE HYDROFOILS EN HUN GEBRUIK:
Hydrofoils zijn zeer populair geworden. Zij worden gebruikt in divers soort zee reizen, van militair gebruik aan watersport. De hoge snelheid, soepele cruise en betere bochten geleverd door draagvleugelboten zijn gebruikt in militaire schepen. De zeilsport heeft ook de draagvleugelboten goedgekeurd om meer snelheid te krijgen. Zij maken nieuwe uitvindingen mogelijk die tegemoet kunnen komen aan de wens van de mensen om het gevaar uit te dagen, zoals de sky ski. Dit is een waterski waaraan een draagvleugelboot is bevestigd en waarmee men boven het wateroppervlak kan vliegen. Elke dag worden meer draagvleugelboten gebruikt, en in de toekomst, kunnen zij de overheersende methode van reizen over zee zijn.
REFERENTIES/Meer INFORMATIE:
Zie ook op deze plaats: Airfoil, Zeilboten
Alexander, Alan, James Grogono, en Donald Nigg; Hydrofoil Sailing. JuanitaKalerghi: London, 1972.
Bertin, John and Michael Smith; Aerodynamics for Engineers, Third Ediotion.Prentice Hall: New Jersey, 1998.
Hook, Cristopher and A.C. Kermode; Hydrofoils. Pitman Paperbags: London, 1967.
The International Hydrofoil Societys Web Page:http://www.erols.com/foiler/index.html
