Die Lotka-Volterra-Gleichungen beschreiben ein ökologisches Räuber-Beute- (oder Parasit-Wirt-) Modell, das davon ausgeht, dass, für eine Reihe fester positiver Konstanten 
(die Wachstumsrate der Beute), 
(die Rate, mit der Raubtiere die Beute vernichten), 
(die Todesrate der Raubtiere) und 
(die Rate, mit der sich Raubtiere durch den Verzehr von Beute vermehren) die folgenden Bedingungen gelten.
1. Eine Beutetierpopulation 
nimmt mit einer Rate 
(proportional zur Anzahl der Beutetiere) zu, wird aber gleichzeitig von Raubtieren mit einer Rate 
(proportional zum Produkt aus der Anzahl der Beutetiere und der Anzahl der Raubtiere) zerstört.
2. eine Raubtierpopulation 
nimmt mit einer Rate 
ab (proportional zur Anzahl der Raubtiere), aber mit einer Rate 
zu (wiederum proportional zum Produkt aus der Anzahl der Beutetiere und der Raubtiere).
Das ergibt die gekoppelten Differentialgleichungen
 |
 |
 |
(1)
|
 |
 |
 |
(2)
|
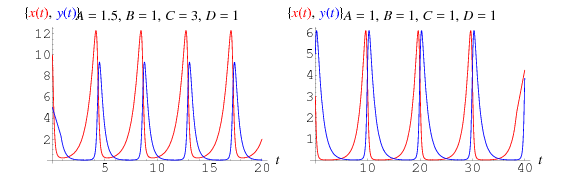
deren Lösungen oben eingezeichnet sind, wobei die Beutetiere in rot und die Räuber in blau dargestellt sind. Bei dieser Art von Modell liegt die Beutekurve immer vor der Raubtierkurve.
Kritische Punkte treten auf, wenn 
, so
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
Der einzige stationäre Punkt befindet sich also bei 
.