Wie bei einem Kuchen kann man 2 kleine Stücke oder ein doppelt so großes Stück haben und es ist die gleiche Menge. Daher sind viele Brüche gleichwertig, wie 2/5 und 4/10.


Jede Zahl kann als Bruch geschrieben werden
Schreibe jede ganze Zahl über 1, um sie zu einem Bruch zu machen, da die Gesamtzahl der Teile in jedem ungeteilten Ganzen eins ist.
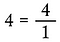
Brüche gerade multiplizieren
Brüche zu multiplizieren ist einfach, multipliziere einfach geradeaus.
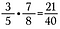
Hinweis: Gemischte Zahlen müssen erst in unechtere Brüche umgewandelt werden, mehr dazu im Folgenden.
Multipliziere mit jeder Form von Eins
Die Zahl 1 wird als multiplikative Identität bezeichnet, weil wir sie mit jeder Zahl multiplizieren können und die Zahl gleich bleibt. Das ist wichtig für Brüche, weil wir oft das Aussehen eines Bruchs ändern müssen, ohne seinen Wert zu ändern.
Zum Beispiel kann ich 1/3 in den entsprechenden Bruch 3/9 umwandeln, indem ich mit 3/3 multipliziere.
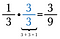
Gleich große Teile addieren und subtrahieren
Beim Addieren und Subtrahieren von Brüchen müssen die Nenner gleich sein. Das macht Sinn. Wenn wir Teile kombinieren oder wegnehmen wollen, muss es sich um gleich große Teile handeln, sonst wird es verwirrend.
Was machst du also, wenn deine Brüche nicht gleich groß sind?
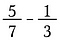
Multipliziere mit einer Form von eins, um die Nenner auf eine gemeinsame Größe zu bringen. Im Grunde genommen teilen wir die Brüche in kleinere Stücke, bis sie die gleiche Größe haben. Dies nennt man das Finden eines gemeinsamen Nenners.
Eigentlich ist jeder gemeinsame Nenner geeignet, aber man zieht es vor, den kleinsten zu finden. In diesem Fall ist die kleinste Zahl, in die sowohl 7 als auch 3 ohne Rest hineingehen, 21. Multipliziere also den ersten Bruch mit 3/3 und den zweiten mit 7/7.
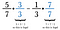
Wenn dir der kleinste gemeinsame Nenner nicht einfällt, kannst du immer jeden Bruch mit dem entgegengesetzten Nenner multiplizieren. Manchmal, wie in diesem Fall, stellt sich heraus, dass dies der kleinste gemeinsame Nenner ist. Ist dies nicht der Fall, reduziere einfach deine Antwort am Ende.
Wenn die Nenner übereinstimmen, subtrahiere die Zähler, um 8/21 zu erhalten.
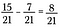
Das funktioniert wie erwartet. Bildlich gesprochen, beginne mit 15 Stücken von insgesamt 21.

Entferne die Färbung von 7 der 15 blauen Blöcke.

Was erwartungsgemäß 8/21 ergibt.
Erst gemischte Zahlen austauschen
Eine gemischte Zahl ist die Kombination aus einer ganzen Zahl und einem Bruch.
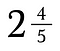
Gemischte Zahlen vertragen sich nicht gut mit anderen Brüchen. Es ist eine gute Idee, sie zuerst in unechtere Brüche umzuwandeln.
Hinweis: Ein unechter Bruch ist ein Bruch, dessen Zähler größer ist als sein Nenner und der deshalb einen Wert größer als eins hat.
Die Umwandlung einer gemischten Zahl ist eine echte Addition
Um 2 und 4/5 in einen unechter Bruch umzuwandeln, addiere 2 + 4/5.
Schritt 1: Schreibe 2 zunächst als 2/1 um.
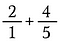
Schritt 2: Multipliziere 2/1 mit 5/5, um einen äquivalenten Bruch von 10/5 zu erhalten, der den gewünschten gemeinsamen Nenner von 5 hat.
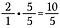
Schritt 3: Addiere 10/5 + 4/5.
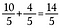
Unser Ergebnis ist der äquivalente uneigentliche Bruch 14/5.
Um in eine gemischte Zahl zurückzukehren, führe die Division durch. Zum Beispiel geht 5 zweimal in 14 ein (da 5 x 2 = 10), wobei 4 Stücke übrig bleiben.
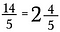
Vergleiche Brüche mit dem Kreuzprodukt
Angenommen, wir wollen herausfinden, welcher größer ist: 5/12 oder 6/13.
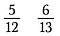
Schritt 1: Multipliziere eine Diagonale und schreibe das Produkt über den Zähler.
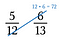
Schritt zwei: Multipliziere die andere Diagonale und schreibe das Produkt über den Zähler.
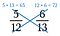
Schritt drei: Vergleichen Sie die Produkte. Die Seite mit dem größeren Produkt ist der größere Bruch. In diesem Fall ist also 5/12 kleiner als 6/13.
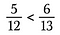
Wir können auch mit Kreuzprodukten feststellen, ob Brüche gleich sind.
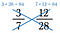
Das Kreuzprodukt von 3/7 und 12/28 ist beides 84, also ist 3/7 = 12/28.
Alles streichen, was durch Eins teilbar ist
Das Beste an Brüchen ist, dass man viele Möglichkeiten zum Streichen findet. Das macht sie schnell und einfach zu handhaben.
Angenommen, ich habe den Bruch 8/10. Sowohl 8 als auch 10 können mit 2 als Faktor umgeschrieben werden.
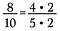
Da 2/2 = 1 ist, kann ich die 2 streichen und 4/5 als reduzierten Bruch übrig lassen.
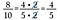
Nutzen Sie diese Strategie, um auch das Multiplizieren von Brüchen zu erleichtern.
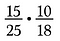
Beginne damit, jede Zahl in Faktoren umzuschreiben.
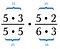
Streiche alle Zahlenpaare, die sich durch 1 teilen. Zum Beispiel 5/5 = 1.
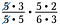
Ich habe noch ein Paar 5er und ein Paar 3er, die sich ebenfalls durch 1 teilen.
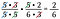
Oops! Ich hätte 6 als 2 x 3 umschreiben und ein Paar 2er streichen können. Es ist in Ordnung, wenn du einen Faktor übersiehst, mach einfach weiter, bis du alle hast.
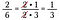
Hätte ich 15/25 mal 10/18 direkt multipliziert, wäre das eine Menge Rechenarbeit gewesen, mit dem Streichen reduziere ich die Brüche vor und mache es einfacher zu multiplizieren.
Multiplikation zum Dividieren von Brüchen verwenden
Das Konzept des Dividierens von Brüchen ist mit einfachen Beispielen wie:

Ein Ganzes hat zwei Hälften, also gibt es 10 Hälften in 5 Ganzen.
Aber bei komplizierteren Brüchen wird das Konzept knifflig.
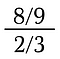
Um dieses Problem zu lösen, nutzen wir zwei Fakten:
- Wir können mit jeder Form von Eins multiplizieren (d.d. h. irgendetwas über sich selbst)
- Multiplizieren mit dem Kehrwert von 3/2, also 2/3, ergibt 1 durch Aufheben
Schritt eins: Beginne damit, mit dem Kehrwert über sich selbst zu multiplizieren.
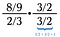
Nun haben wir zwei kleinere Probleme zu lösen (blau und grün).
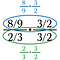
Schritt zwei: Streiche alles, was in der unteren (grünen) Fraktion durch 1 geteilt wird. Das sollte immer 1 ergeben.

Jetzt bleibt noch das obere Problem zu lösen.
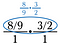
Schritt drei: Benutze das Stornieren, um den Bruch vorzureduzieren. Nach diesen Kürzungen multiplizierst du quer, um 4/3 zu erhalten.

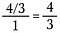
Verknüpfung
Dies ist die Langhandmechanik von „umdrehen und multiplizieren.“
Wir können das Multiplizieren mit dem Kehrwert unten überspringen, da er sich immer zu 1 aufhebt. Daher musst du nur den Zähler mit dem Kehrwert des Nenners multiplizieren.

Bonus: Theorie, falls es dich interessiert…
Gute Frage! Um zu verallgemeinern, mache zwei Brüche mit den Buchstaben a, b, c und d, um vier verschiedene Zahlen darzustellen.
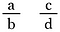
Multipliziere beide Brüche mit b-d (so können wir die Nenner aufheben).
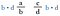
Nun heben wir die b’s auf der linken Seite und die d’s auf der rechten Seite auf, da sie sich durch 1 teilen. Wir haben keine Brüche mehr, sondern nur noch die Produkte d-a und c-b.
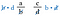
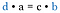
Betrachten wir wieder die ursprünglichen Brüche. Es sind die gleichen Produkte, als ob wir die Diagonalen multipliziert hätten. Daher besteht die Abkürzung darin, das Kreuzprodukt zu vergleichen.
❤ STAY CONNECTED ❤
Bleibe auf dem Laufenden mit allem, was Math Hacks macht!