Einführung
Diese Seite gibt einen Überblick über die Kontinuitätsgleichung, die die Erhaltung der Masse in einer Eulerschen Analyse erzwingt. Es handelt sich dabei nicht um eine Beschreibung des Materialverhaltens im engeren Sinne, aber die sich daraus ergebende Gleichung wird häufig als Identität verwendet, um konstitutive Modelle, die das Materialverhalten beschreiben, algebraisch zu manipulieren. Es lohnt sich also, sie zu überprüfen. Sie ist auch für die Analyse von Flüssigkeitsströmungen von zentraler Bedeutung, da klassische Flüssigkeitsanalysen nicht Lagrange sein können, da die Positionen aller Flüssigkeitsteilchen zu \(t = 0\) unbekannt sind.
Massenerhaltung
Die Kontinuitätsgleichung spiegelt die Tatsache wider, dass die Masse in jeder nicht-nuklearen Kontinuumsmechanikanalyse erhalten bleibt. Die Gleichung wird entwickelt, indem die Geschwindigkeit, mit der die Masse in ein Kontrollvolumen hinein- und aus ihm herausfließt, addiert wird und der Nettozufluss gleich der Änderungsrate der Masse in diesem Volumen gesetzt wird. Dies wird in der nachstehenden Abbildung veranschaulicht.
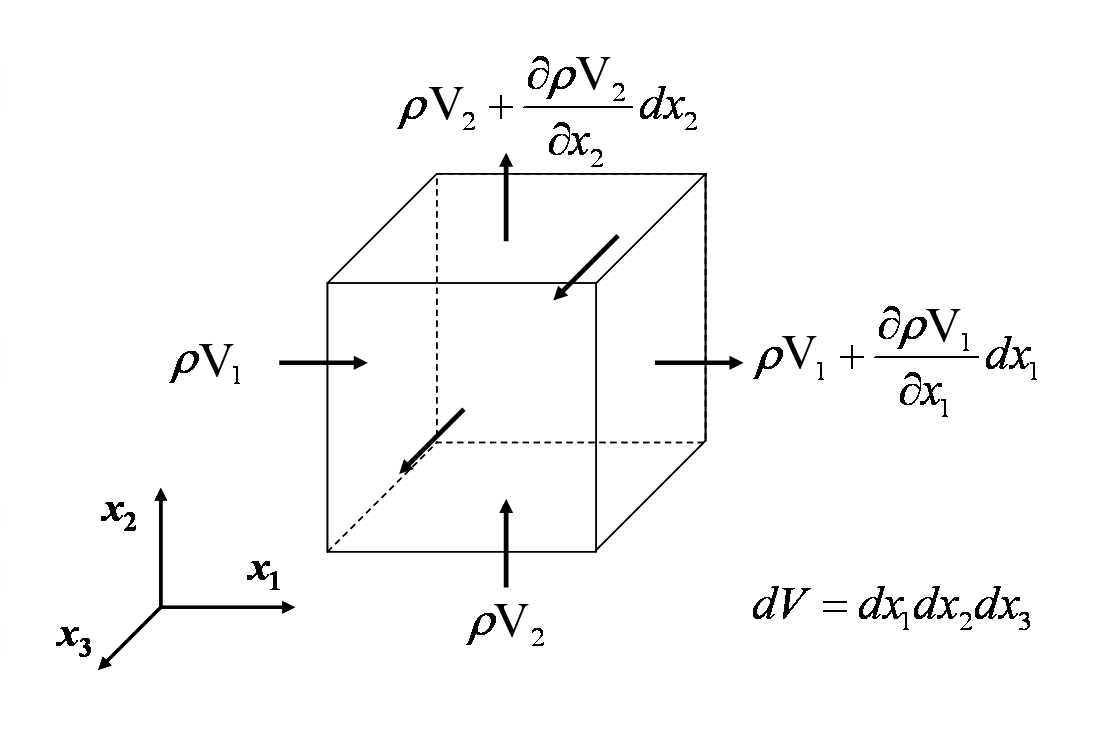
Die Gleichsetzung aller Massenströme in das und aus dem Differentialregelvolumen ergibt
\
Die Terme streichen und durch \(dx_1 dx_2 dx_3\) dividieren ergibt
\
und durch Umformung erhält man
\
Dies lässt sich kurz und bündig schreiben als
\

Wichtige Punkte
Dies sind die endgültigen, vollständige und allgemeinste Form der Kontinuitätsgleichung, die die Erhaltung der Masse erzwingt. Sie gilt für alle Stoffe, nicht nur für Flüssigkeiten. Sie gilt also auch für Festkörper. Man beachte, dass es sich um eine einzelne Skalargleichung handelt und dass sie eulerscher Natur ist, da die Gradiententerme \({\teilweise \über \teilweise x_i}\) und nicht \({\teilweise \über \teilweise X_i}\) lauten.
Man könnte sich fragen, ob es ein Lagrange-Gegenstück zur eulerschen Form dieser Gleichung gibt. There is. Gewöhnlich wird sie geschrieben als
\
Dies besagt einfach, dass der Differentialanteil der Masse im verformten Zustand\(\rho \, dV_o\) gleich seinem ursprünglichen Wert\(\rho_o dV_o\) im unverformten Zustand sein muss.
Es gibt mehrere Sonderfälle der Kontinuitätsgleichung. Der erste tritt auf, wenn die Strömung stationär ist. In diesem Fall ist die Ableitung nach der Zeit gleich Null und es bleibt übrig.
\
Der zweite Sonderfall ist der der Inkompressibilität, d.h., \In diesem Fall ist die Ableitung nach der Zeit gleich Null und \(\rho\) kann aus der Gleichung herausgerechnet werden, so dass nur
\
übrig bleibt.
\
Beachten Sie, dass dies nichts anderes ist als \(\text{tr}({\bf D}) = 0\) für den Fall inkompressibler Materialien.

Materialableitung
Das Folgende ist erwähnenswert, weil es die Trennung von Dichte- und Geschwindigkeitsvektor erlaubt. Der erste Schritt ist die Anwendung der Produktregel auf den Divergenzterm in der Kontinuitätsgleichung.
\
Und dann ist zu beachten, dass\({\partial \rho \über \partial t} + {\bf v} \cdot \nabla \rho\) nur die materielle Ableitung der Dichte,\({D \rho \über D t}\) ist.
Die Kontinuitätsgleichung kann also auch geschrieben werden als
\
Wenn das Material inkompressibel ist, dann kann sich \(\rho\) nicht ändern, also muss \( {D \rho \über D t} \) Null sein, Bleibt
\
Und dividiert man dann durch \(\rho\) (da es nicht Null ist), erhält man
\

Kontinuitätsgleichung Beispiel
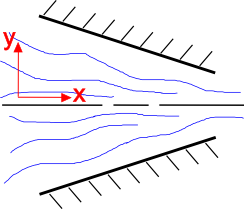
Es ist intuitiv, dass der Flüssigkeitsstrom schneller wird, wenn sich die Querschnittsfläche verkleinert, wie rechts dargestellt. Die Kontinuitätsgleichung erklärt dies. Die Kontinuitätsgleichung für ein stationäres 2-D-Strömungsfeld eines inkompressiblen Fluids lautet:
\
Betrachten Sie zunächst die y-Komponente der Strömung, \(v_2\). Die Geometrie der konvergierenden Düse zwingt die \(v_2\)-Komponente dazu, nach oben zu fließen, wenn \(y \lt 0\), und nach unten zu fließen, wenn \(y \gt 0\). Also \(v_2 \gt 0\), wenn\(y \lt 0\) und \(v_2 \lt 0\), wenn \(y \gt 0\).
Dies führt dazu, dass \({\partial v_2 \über \partial x_2} \lt 0\) in der konvergierenden Düse.
Aber die Kontinuitätsgleichung schreibt vor, dass die Summe der beiden partiellen Ableitungen gleich Null sein muss. Wenn also die zweite kleiner als Null ist, dann
\
Und das bedeutet, dass die Strömung beschleunigt werden muss.